Petit devoir sur les suites et la récurrence

Un soin particulier sera apporté à la rédaction.

L'usage de la calculatrice n'est pas autorisé.

Durée : 30 minutes

Exercice 1

Soit la suite \((u_n)\) définie sur \(\mathbb{N}\) par \(u_0 =\dfrac{1}{2}\) et, pour tout \(n \in \mathbb{N}\), \(u_{n+1} = \dfrac{2u_n}{1 + u_n}\).

1. Calculer \(u_1\) que l'on écrira sous la forme d’une fraction irréductible.

   Corrigé

   \(u_1=\dfrac{2 \times \dfrac{1}{2} }{1+\dfrac{1}{2}}\)

   \(\Leftrightarrow u_1=\dfrac{1}{\dfrac{3}{2}}\)

   \(\Leftrightarrow u_1=\dfrac{2}{3}\)

2. Démontrer par récurrence que, pour tout entier naturel \(n\) : \(u_n = \dfrac{2^n}{1+2^n}\).

   Corrigé

   Soit \(P_n : u_n = \dfrac{2^n}{1+2^n}\)

   Initialisation

   \(\dfrac{2^0}{1+2^0}=\dfrac{1}{1+1}=\dfrac{1}{2}\) et \(u_0=\dfrac{1}{2}\)

   Donc \(P_0\) est vraie.

   Hérédité

   Supposons \(\text P_n\) vraie pour un rang donné, montrons qu'alors \(\text P_{n+1}\) est vraie.

   On a \(u_n = \dfrac{2^n}{1+2^n}\) et \(u_{n+1}=\dfrac{2u_n}{1 + u_n}\)

   \(\Rightarrow u_{n+1}=\dfrac{2\dfrac{2^n}{1+2^n}}{1 + \dfrac{2^n}{1+2^n}}\)

   \(\Rightarrow u_{n+1}=\dfrac{\dfrac{2^{n+1}}{1+2^n}}{\dfrac{1+2^n+2^n}{1+2^n}}\)

   \(\Rightarrow u_{n+1}=\dfrac{2^{n+1}}{1+2^n+2^n}\)

   \(\Rightarrow u_{n+1}=\dfrac{2^{n+1}}{1+2 \times 2^n}\)

   \(\Rightarrow u_{n+1}=\dfrac{2^{n+1}}{1+2^{n+1}}\)

   \(P_{n+1}\) est vraie

   Conclusion

   On a \(\text P_0\) vraie et \(\text P\) héréditaire, donc, par récurrence sur \(n\), \(\text P_n\) est vraie pour tout \(n \in \mathbb{N}\).

Exercice 2

Soit la suite \((u_n)\) définie sur \(\mathbb{N}\) par \(\left\{ \begin{matrix}{ { u_{0} = 1\phantom{aaaa ' }}} \\ { {u_{n + 1} = \sqrt{u_n^2+3}}} \end{matrix} \right.\)

1. Sur le graphique ci-dessous, on a représenté la courbe représentative de la fonction \(f\), notée \(C_f\) de la fonction \(f : x \mapsto \sqrt{x^2+3}\).

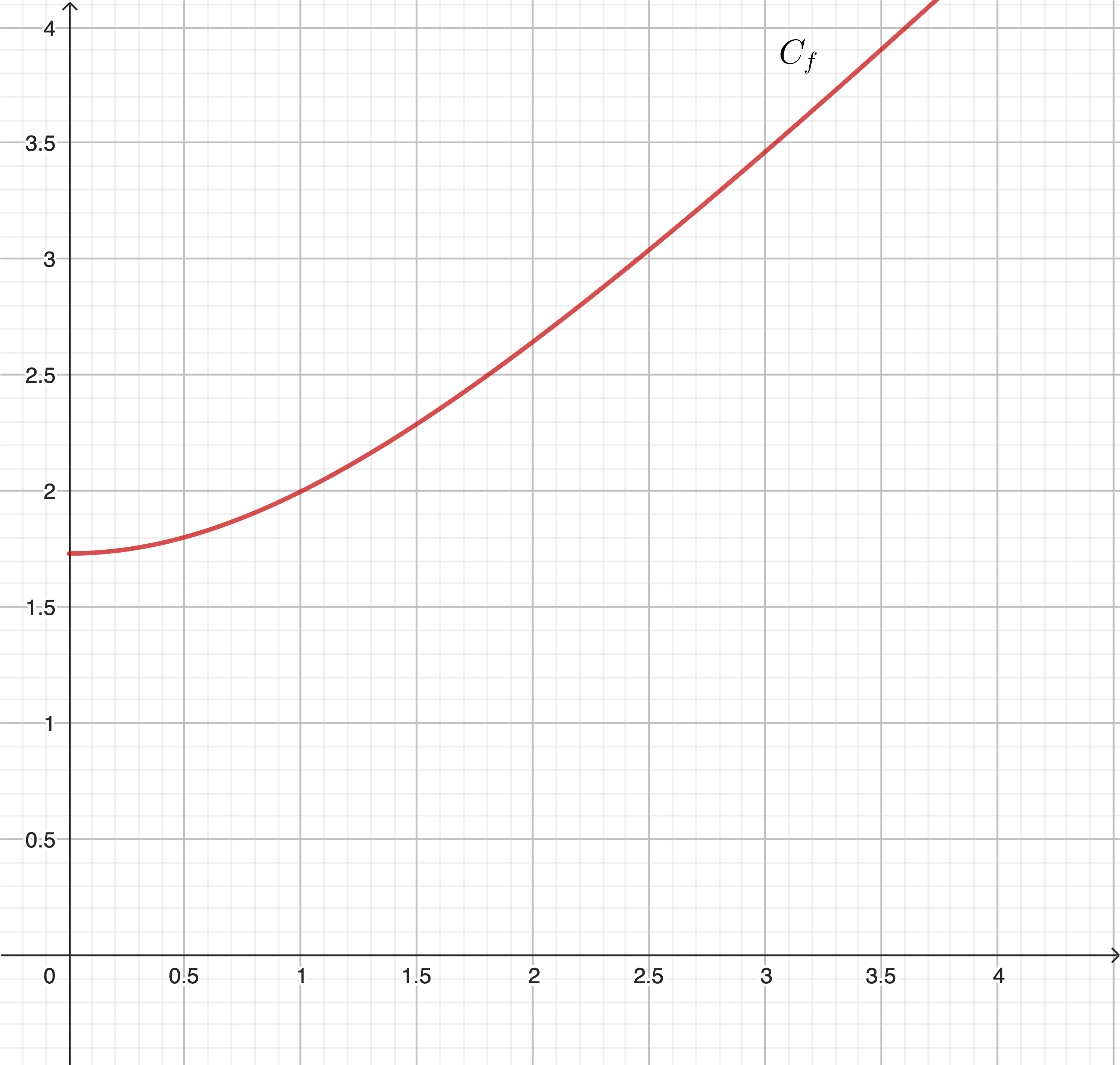
   a) Construire sur le graphique \(u_1\), \(u_2\) et \(u_3\).

   b) Quelles conjectures peut-on formuler sur le comportement de \((u_n)\) ?

   Corrigé

   

   \((u_n)\) semble être une suite croissante tendant vers \(+\infty\).

2. a) Calculer \(u_1\), \(u_2\) et \(u_3\).

   Corrigé

   \(u_1=\sqrt{u_0^2+3}=\sqrt{1+3}=\sqrt{4}=2\)

   \(u_2=\sqrt{u_1^2+3}=\sqrt{4+3}=\sqrt{7}\)

   \(u_3=\sqrt{u_2^2+3}=\sqrt{7+3}=\sqrt{10}\)

   b) La suite \((u_n)\) est-elle arithmétique ?

   Corrigé

   \(u_1-u_0=2-1=1\) et \(u_2-u_1=\sqrt{7}-2\) donc \(u_1-u_0 \neq u_2-u_1\)

   La suite \((u_n)\) n'est pas arithmétique.

3. On suppose que pour tout \(n \in \mathbb{N}\), \(u_n\) est positif et on pose \(v_n = {u_n}^2\)

   a) Montrer que \((v_n)\) est une suite arithmétique et préciser sa raison et son premier terme.

   Corrigé

   \(v_{n+1}-v_n=u_{n+1}^2-u_n^2\)

   \(\Leftrightarrow v_{n+1}-v_n=\sqrt{u_n^2+3}^2-u_n^2\)

   \(\Leftrightarrow v_{n+1}-v_n={u_n^2+3}-u_n^2\)

   \(\Leftrightarrow v_{n+1}-v_n=3\)

   La suite \((v_n)\) est donc arithmétique de raison \(3\).

   Son premier terme est \(v_0=u_0^2=1\)

   b) Exprimer \(v_n\) en fonction de \(n\) puis déduire \(u_n\) en fonction de \(n\).

   Corrigé

   D'après ce qui précède, on peut écrire la forme explicite de \((v_n)\):

   \(v_n=v_0 + n \times r=1+3n\)

   \(u_n=\sqrt{v_n}=\sqrt{1+3n}\) pour \(n \in \mathbb{N}\)