Petit DS sur les suites
L’usage de la calculatrice, bien que totalement inutile, est autorisé.
Durée : 31 min
On définit une suite \((u_n)\) par \(u_0=3\) et pour tout \(n \in ℕ\) , \(u_{n+1}=\frac{3u_n}{3+2u_n}\) .
-
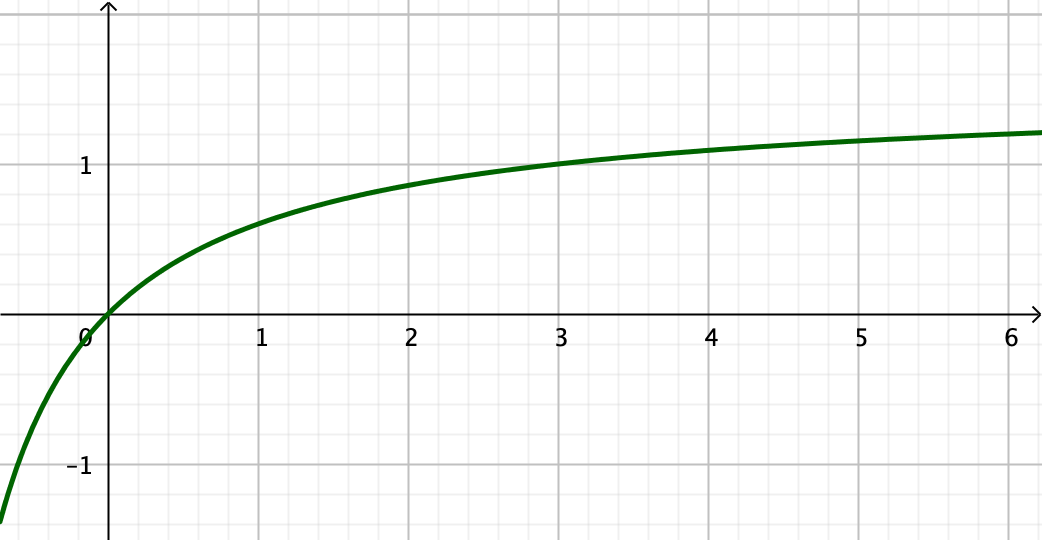
On donne au dos de cette feuille la courbe représentative de la fonction \(f\) définie par \(f(x)=\frac{3x}{3+2x}\) sur \(\mathbb{R}^{+}\).
Construire, sur l’axe des abscisses, les valeurs \(u_0\) , \(u_1\) , \(u_2\) et \(u_3\) en laissant apparents les tracés nécessaires à la construction.
-
Montrer par récurrence que, pour tout \(n \in ℕ\) , \(u_n \geqslant 0\) .
-
Montrer que la suite \((u_n)\) est décroissante.
-
On pose maintenant pour tout \(n\) : \(v_n=\frac 3{u_n}\). Montrer que \((v_n)\) est une suite arithmétique.
-
En déduire l’expression de \(v_n\) puis de \(u_n\) en fonction de \(n\) .
-
Représentation graphique.
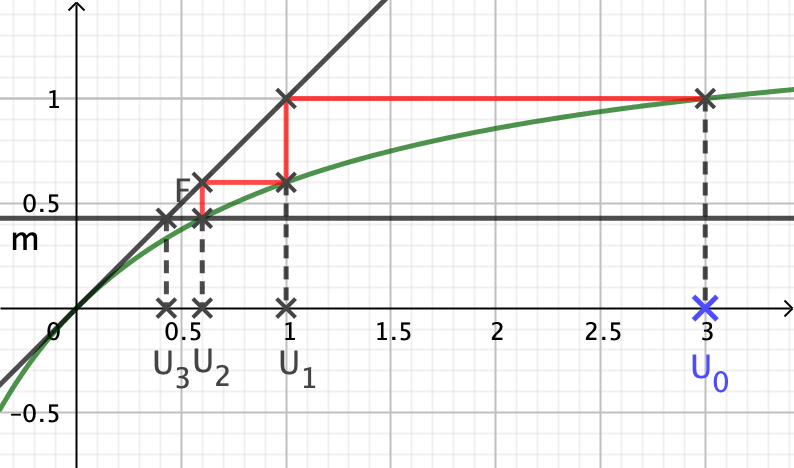
-
Soit \(\text P(n)\) : \(\text{«}u_n\geqslant 0\text{»}\) :
Initialisation
On a \(u_0=3\) et \(3\geqslant 0\) donc \(\text P(0)\) est vérifiée.
Hérédité
Supposons \(\text P(n)\) vraie pour un rang n donné et montrons qu’alors \(\text P(n+1)\) est vraie.
\(u_n\geqslant 0\) ⇒ \(3u_n\geqslant 0\) \((1)\) et \(u_n\geqslant 0\) ⇒ \(2u_n\geqslant 0\) ⇒ \(2u_n+3\geqslant 3\) ⇒ \(2u_n+3>0\) \((2)\) .
Avec \((1)\) et \((2)\) , on a \(\frac{3u_n}{2u_n+3}\geqslant 0\) soit \(u_{n+1}\geqslant 0\)
P(n+1) est donc vérifiée.
Conclusion
\(\text P(0)\) est vérifiée et P est héréditaire. Par récurrence sur \(n\) , on a donc \(u_n\geqslant 0\) pour tout \(n \in ℕ\) .
-
\(u_n\geqslant 0\) ⇒ \(3+2u_n\geqslant 3\) . De plus, \(\frac{u_{n+1}}{u_n}=\frac 3{3+2u_n}\) . Donc \(\frac{u_{n+1}}{u_n}\leqslant 1\) .
Les termes de la suite \((u_n)\) étant positifs, \((u_n)\) est une suite décroissante.
-
\(v_{n+1}=\frac 3{u_{n+1}}=\frac 3{\frac{3u_n}{3+2u_n}}=\frac{3+2u_n}{u_n}=\frac 3{u_n}+2=v_n+2\) .
\((v_n)\) est donc une suite arithmétique de raison \(2\) et de premier terme \(v_0=\frac 3{u_0}=\frac 3 3=1\) .
-
On a donc \(v_n=v_0+n\times r=1+2n\) et \(u_n=\frac 3{v_n}=\frac 3{1+2n}\) .