Petit devoir dans l'Espace
Un soin particulier sera apporté à la rédaction et à la justification.
L'usage de la calculatrice est autorisé.
Le barème est donné à titre indicatif.
Durée : 40 minutes
Exercice 1
On considère les points \(\text{A}(0; 1; 2)\), \(\text{B}(1; 2; 3)\) et les vecteurs \(\vec{u}\) \(\left( \begin{array}{c} 1 \\ 1 \\ 1 \\ \end{array} \right)\) et \(\vec{v} \left( \begin{array}{c} -1 \\ 2 \\ 1 \\ \end{array} \right)\).
-
Donner une représentation paramétrique de la droite \((d)\) passant par \(\text{A}\) et de vecteur directeur \(\vec{u}\).
-
Donner une représentation paramétrique de la droite \((d')\) passant par \(\text{B}\) et de vecteur directeur \(\vec{v}\).
-
Le point \(\text{C}(6;-8;-2)\) appartient-il à \((d)\) ? à \((d')\) ?
-
Quelle est la position relative des droites \((d)\) et \((d')\) ?
Exercice 2
\(\text{SABCD}\) est une pyramide dont la base \(\text{ABCD}\) est un carré. \(\text{I}\) et \(\text{J}\) sont des points des arêtes \([\text{SA}]\) et \([\text{SC}]\) tels que \(\overrightarrow{SI}=\dfrac{1}{4}\overrightarrow{SA}\) et \(\overrightarrow{SJ}=\dfrac{1}{4}\overrightarrow{SC}\) et K est un point tel que \(\overrightarrow{DK}=\dfrac{3}{4}\overrightarrow{DB}\).
- Faire une figure en perspective cavalière.
- Prouver que les droites \((IJ)\) et \((AC)\) sont parallèles.
- Déterminer et construire sur la figure l’intersection des plans \((IJK)\) et \((ABC)\) à l’aide d'un théorème (justifier).
- Construire les sections des faces ABC, SBC et SAB avec le plan \((IJK)\). On repassera la réponse en couleur rouge.
- Terminer la section du plan \((IJK)\) avec la pyramide.
bonus: donner une démonstration du théorème de la question 3
Exercice 1
-
Représentation paramétrique de \((d)\)
\((d)\) : \(\begin{cases} x=0+t\\ y=1+t \\ z=2+t \\ \end{cases} \quad, t\in \mathbb{R}\)
-
Représentation paramétrique de \((d')\)
\((d')\) : \(\begin{cases} x=1-k\\ y=2+2k \\ z=3+k \\ \end{cases} \quad, k\in \mathbb{R}\)
-
On souhaite déterminer \(t\) tel que:
\(\begin{cases} 6=0+t\\ -8=1+t \\ -2=2+t \\ \end{cases} \Rightarrow \begin{cases} 6=t\\ -9=t \\ -4=t \\ \end{cases}\) Ce qui est absurde.
Par conséquent \(C \notin (d)\)
De même on veut résoudre: \(\begin{cases} 6=1-k\\ -8=2+2k \\ -2=3+k \\ \end{cases} \Rightarrow \begin{cases} -5=k\\ -5=k \\ -5=k \\ \end{cases}\)
D'où \(C \in (d')\)
-
On a \(C \in (d')\) et \(C \notin (d)\) donc les droites ne sont pas confondues.
De plus \(\dfrac{-1}{1} \ne \dfrac{2}{1}\) donc les vecteurs \(\vec{u}\) et \(\vec{v}\) ne sont pas colinéaires. Les droites \((d)\) et \((d')\) ne sont pas parallèles.
Déterminons si les droites \((d)\) et \((d')\) sont sécantes.
S'il existe un point \(M\) tel que \(M(x;y;z)=(d) \cap (d')\) alors les coordonnées de ce point vérifient:
\(\begin{cases} x=1-k=t \\ y=2+2k=1+t \\ z=3+k=2+t \\ \end{cases}\) \(\Rightarrow \begin{cases} 1-k=t\\ 2+2k=1+t \\ 3+k=2+t \\ \end{cases}\) \(\Rightarrow \begin{cases} t+k=1 \\ t-2k=1 \\ t-k=1 \\ \end{cases}\) \(\Rightarrow \begin{cases} 2t=2 \\ t-2k=1 \\ 2k=0 \\ \end{cases}\)
La deuxième équation est bien vérifiée pour \(k=0\) et \(t=1\).
Les droites \((d)\) et \((d')\) sont donc sécantes (en \(B\)).
Exercice 2
-
Figure
Ci-dessous la version complète de la figure (sans la question 5.)
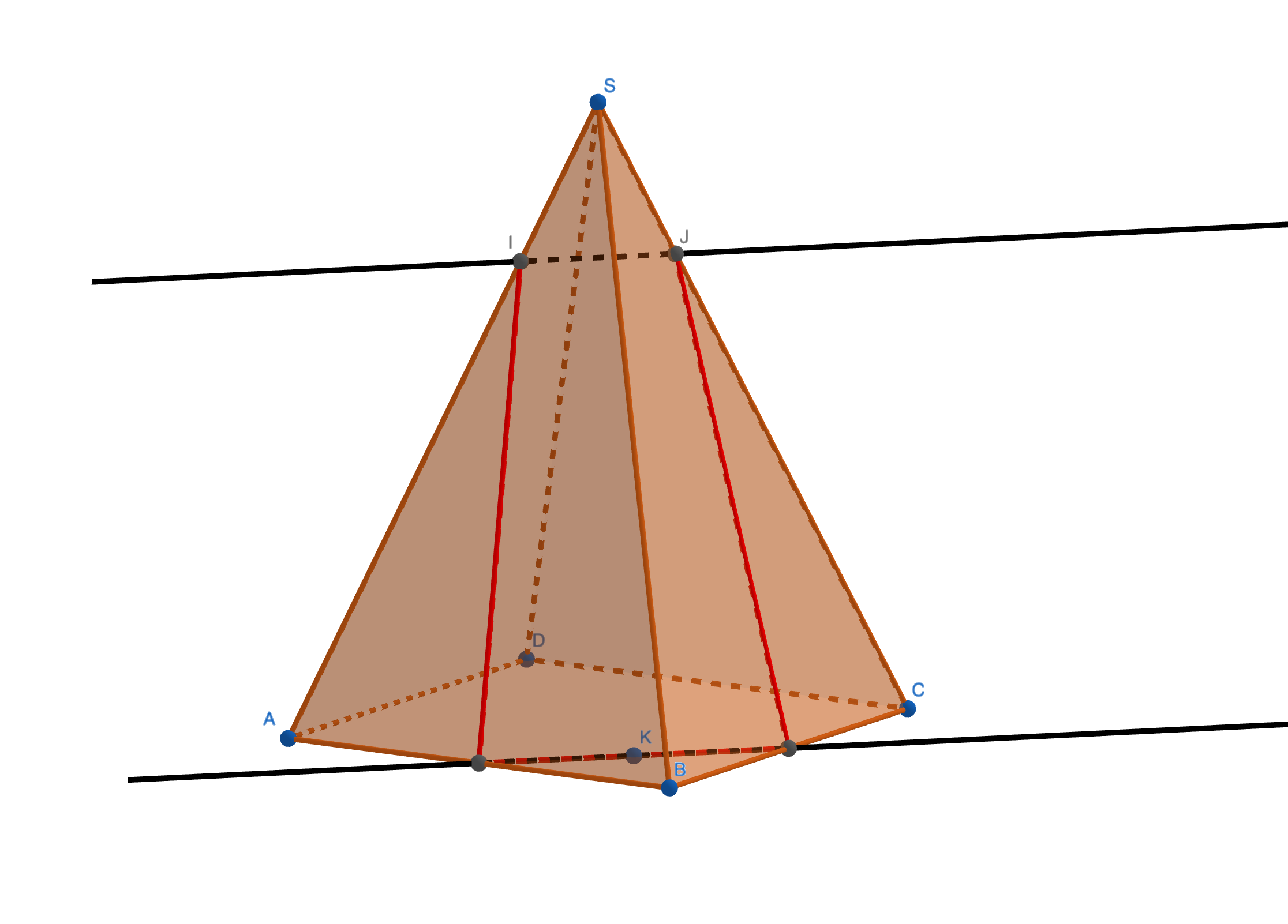
-
On a \(\overrightarrow{SI}=\dfrac{1}{4}\overrightarrow{SA}\) et \(\overrightarrow{SJ}=\dfrac{1}{4}\overrightarrow{SC}\) donc \(\dfrac{SI}{SA}=\dfrac{SJ}{SC}\).
De plus les points S, I et A sont alignés et les points S, J et C sont alignés dans le même ordre.
D'après la réciproque du théorème de Thalès, les droites \((IJ)\) et \((AC)\) sont parallèles.
-
Les droites \((IJ)\) et \((AC)\) sont parallèles et sont contenues respectivement dans les plans \((IJK)\) et \((ABC)\), d'après le théorème du toit, l'intersection de ces deux plans est une droite parallèle à \((IJ)\) et \((AC)\).
De plus \(K \in (IJK)\) et \(K \in (ABC)\) donc \(K \in (ABC) \cap (IJK)\).
On trace donc une parallèle à \((IJ)\) passant par \(K\).
-
Voir le graphique ci-dessus.
-
Graphique ci-dessous.
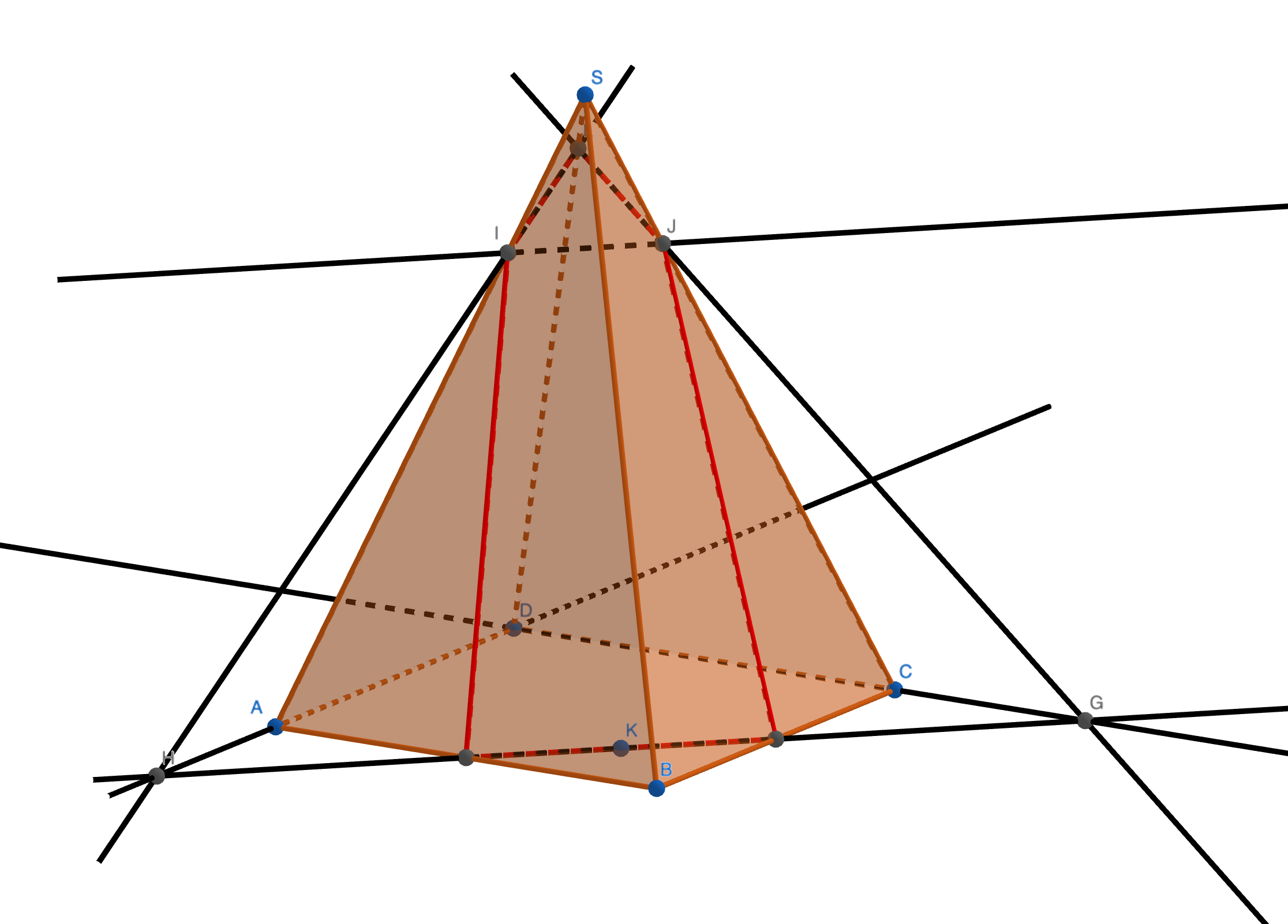
bonus : La démonstration du théorème du Toit est exigible et est donc donnée en cours.