Aller au contenu

Devoir sur les limites et la continuité

L'usage de la calculatrice est autorisé

Un soin particulier sera apporté à la rédaction.

Durée : 50 min

Exercice 1 (3 points)

Dans un repère orthonormé, \(C\) est la courbe représentative de la fonction \(f\) définie sur \(]-2;+\infty[\) par:

\[f(x)=x-\dfrac{x^2-6x+5}{x+2}\]
  1. DĂ©montrer que la courbe \(C\) admet une asymptote verticale \(d\) et donner une Ă©quation de \(d\).
    1. DĂ©terminer une Ă©quation de l'asymptote horizontale \(d'\) Ă  la courbe \(C\).
    2. Étudier la position relative de la courbe \(C\) et de la droite \(d'\).
  1. On a \(x+2\) au dénominateur donc \(x=-2\) est une candidate pour être l'équation de l'asymptote verticale. De plus \(\lim\limits_{\substack{x \to -2 \\ x>-2}}x^2-6x+5=21\), et \(\lim\limits_{\substack{x \to -2 \\ x>-2}}x+2=0^+\) par conséquent \(\lim\limits_{\substack{x \to -2 \\ x>-2}}f(x)=-\infty\) et la droite d'équation \(x=-2\) est bien asymptote à \(C\).

  2. On récrit: \(f(x)=\dfrac{x(x+2)}{x+2}-\dfrac{x^2-6x+5}{x+2}=\dfrac{8x-5}{x+2}\) On calcule \(\lim\limits_{x \to +\infty}\dfrac{8x-5}{x+2}=\lim\limits_{x \to +\infty}\dfrac{8-\frac 5 x}{1+\frac 2 x}\).

    Or \(\lim\limits_{x \to +\infty}\dfrac{5}{x}=\lim\limits_{x \to +\infty}\dfrac{2}{x}=0\), par somme et quotient, on obtient donc \(\lim\limits_{x \to +\infty}f(x)=8\)

    L'asymptote horizontale en \(+\infty\) a pour Ă©quation \(y=8\)

    Position relative:

    On détermine le signe de \(f(x)-8=\dfrac{8x-5}{x+2}-8=\dfrac{8x-5-8x-16}{x+2}=\dfrac{-21}{x+2}\). Sur \(]-2;+\infty[\) cette quantité est négative, donc \(C\) est en dessous de \(d'\).

Exercice 2 (4 points)

Soit \(g\) la fonction définie sur \(\mathbb{R}\) par:

\[g(x)=xe^x-e^x-1\]

  1. Calculer \(\lim\limits_{x \to -\infty} g(x)\) et \(\lim\limits_{x \to +\infty} g(x)\)

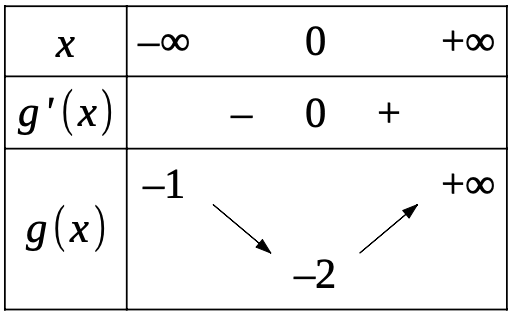
  2. Étudier les variation de \(g\), puis dresser le tableau de variation de \(g\).

  3. Montrer que l’équation \(g(x) = 0\) a une unique solution \(\alpha\) sur \(\mathbb{R}\).

    Donner un encadrement à \(10^{-3}\) de \(\alpha\) à l’aide de l’algorithme de dichotomie. On donnera le nombre d'itérations. On pourra calculer \(g(2)\).

  4. DĂ©montrer que \(e^{\alpha}=\dfrac{1}{\alpha-1}\).

  5. Étudier le signe de \(g(x)\)

  1. On a \(\lim\limits_{x \to -\infty} xe^{x}=0\) et \(\lim\limits_{x \to -\infty} e^x=0\), par somme on a donc \(\lim\limits_{x \to -\infty} g(x)=-1\)

    En \(+\infty\): on récrit \(g(x)=(x-1)e^x-1\)

    \(\lim\limits_{x \to +\infty} e^x=+\infty\) et \(\lim\limits_{x \to +\infty}(x-1)=+\infty\), par produit et somme, on obtient \(\lim\limits_{x \to +\infty} g(x)=+\infty\)

  2. \(g\) est dérivable sur \(\mathbb{R}\) car somme et produit de fonctions dérivables sur \(\mathbb{R}\).

    On a \(xe^x\) qui est de la forme u(x)v(x) avec \(u(x)=x\), \(u'(x)=1\), \(v(x)=e^x\) et \(v'(x)=e^x\) d'oĂą \((xe^x)'=u'(x)v(x)+u(x)v'(x)=e^x+xe^x\)

    On obtient alors \(g'(x)=e^x+xe^x-e^x=xe^x\)

    On a \(e^x>0\) sur \(\mathbb{R}\), donc \(g'(x)\) est du signe de \(x\).

  3. D'après le tableau des variations de \(g\), on a \(g(x)<0\) sur \(\mathbb{R}^-\). \(g(x)=0\) n'admet donc pas de solutions sur \(\mathbb{R}^-\).

    Sur \(\mathbb{R}^+\), on a:

    • \(g\) continue.
    • \(g\) strictement croissante.
    • \(g\) change de signe car \(g(0)=-2\) et \(\lim\limits_{x \to +\infty} g(x)=+\infty\).

    D'après le corollaire du théorème sur les valeurs intermédiaires, l'équation \(g(x)=0\) admet une unique solution sur \(\mathbb{R}^+\), on note cette solution \(\alpha\).

    On a \(g(2)=e^2-1\) strictement positif (car \(e>2\)), donc \(0<\alpha<2\).

    Cet intervalle de recherche de \(\alpha\) étant de longueur \(2\), on doit le diviser par plus de 2000 pour obtenir une valeur approchée de \(\alpha\) à \(10^{-3}\). Si on le divise par \(2^{11}=2048\) cela conviendra. On partage donc 11 fois l'intervalle \([0;2]\) en 2, soit 11 itérations.

    On obtient alors: \(1.278<\alpha<1.279\)

  4. On a \(g(\alpha)=0 \Leftrightarrow \alpha e^{\alpha}-e^{\alpha}-1=0 \Leftrightarrow (\alpha-1)e^{\alpha}=1 \Leftrightarrow e^{\alpha}=\dfrac{1}{\alpha-1}\).

  5. D'après le tableau des variations de \(g\) du 2., on déduit \(g\) négative sur \(]-\infty;\alpha]\) et positive sur \([\alpha;+\infty[\).

Exercice 3 (3 points)

Soit \(f\) la fonction définie sur \(\mathbb{R}\) par :

\[\left\{\begin{matrix}f(x)=x^2(2-x)\text{ }\text{si}\text{ }x \in [0;2[\\f(x)=f(x-2)\text{ }\text{si}\text{ }x \notin [0;2[\end{matrix}\right.\]
  1. Calculer \(f(2)\); la fonction \(f\) est-elle continue en 2 ?
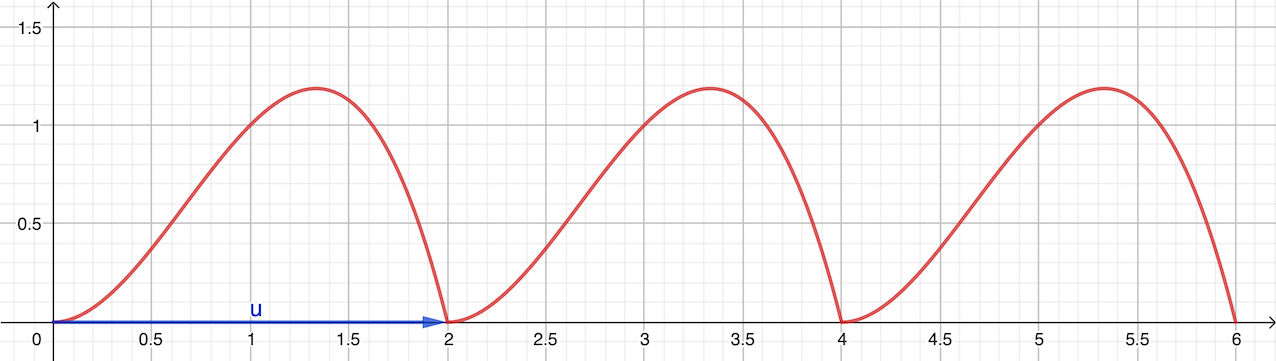
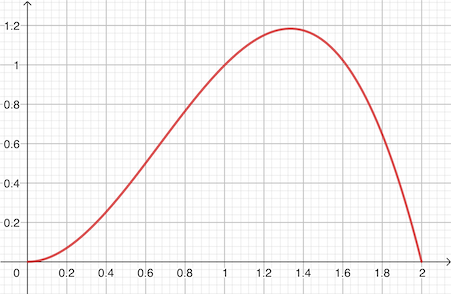
  2. Construire la partie de la courbe représentative de \(f\) sur \([0;2]\) dans un repère orthonormé \((O;\vec \imath,\vec \jmath)\).
  3. Soit \(n \in \mathbb{N}^*\). Comment peut-on déduire la partie de la courbe représentative de \(f\) sur l'intervalle \([2n;2n+2]\) à partir de celle construite dans la question 2. ?

  1. \(f(2)=f(0)=0^2(2-0)=0\)

    On calcule \(\lim\limits_{\substack{x \to 2 \\ x<2}}f(x)=\lim\limits_{\substack{x \to 2 \\ x<2}}x^2(2-x)=0\) (par produit).

    On a \(\lim\limits_{x \to 2}f(x)=f(2)\) donc \(f\) est bien continue en \(2\).

  2. Représentation graphique

  3. On a \(f(x+2)=f(x)\) pour \(x \in [2n;2n+2]\), la courbe représentative de \(f\) sur cet intervalle est donc l'image de la courbe représentative de \(f\) sur \([0;2]\) par la translation de vecteur \(2n\vec \imath\).