Devoir « J'ai dépassé les limites »

L'usage de la calculatrice n'est pas autorisé.

La rédaction est importante. Soyez propre et clair.

Durée: 55 min

SujetCorrigé

Partie A

On appelle  \(f\)  la fonction définie sur \(\mathbb{R}\) par \(f(x)=2\sqrt{x^2+36}-x\) .

1. Étude de \(f\)  en \(-\infty\) :

   1. Déterminer \(\lim\limits_{x\to -\infty }\sqrt{x^2+36}\)  (en justifiant avec soin)

   2. En déduire la limite de \(f\)  en \(-\infty\) .

2. Étude de \(f\)  en \(+\infty\) :

   1. Montrer que, pour tout \(x>0\) , \(f(x)\geqslant x\)

   2. En déduire la limite de \(f\)  en \(+\infty\) .

3. Déterminer l'ensemble de dérivabilité de \(f\) . Calculer \(f'\) .

   Montrer que \(f'(x)<0\)  si \(x\leqslant 0\) .

4. Démontrer que pour tout \(x\) :

   \(\qquad \qquad \qquad \qquad f'(x)=\dfrac{3x^2-36}{(2x+\sqrt{x^2+36})\sqrt{x^2+36}}\).

   En déduire le signe de \(f'(x)\)  pour tout \(x>0\) .

5. Dresser le tableau des variations de \(f\) .

Partie B

On désire construire une canalisation de collecte des eaux pluviales en façade d'une maison, deux tuyaux obliques \(\text{DG}\)  et \(\text{CG}\)  se raccordant à un tuyau vertical \(\text{GE}\) . \(\text E\) , \(\text G\)  sont les milieux respectifs des segments \([\text{AB}]\)  et \([\text{FH}]\).

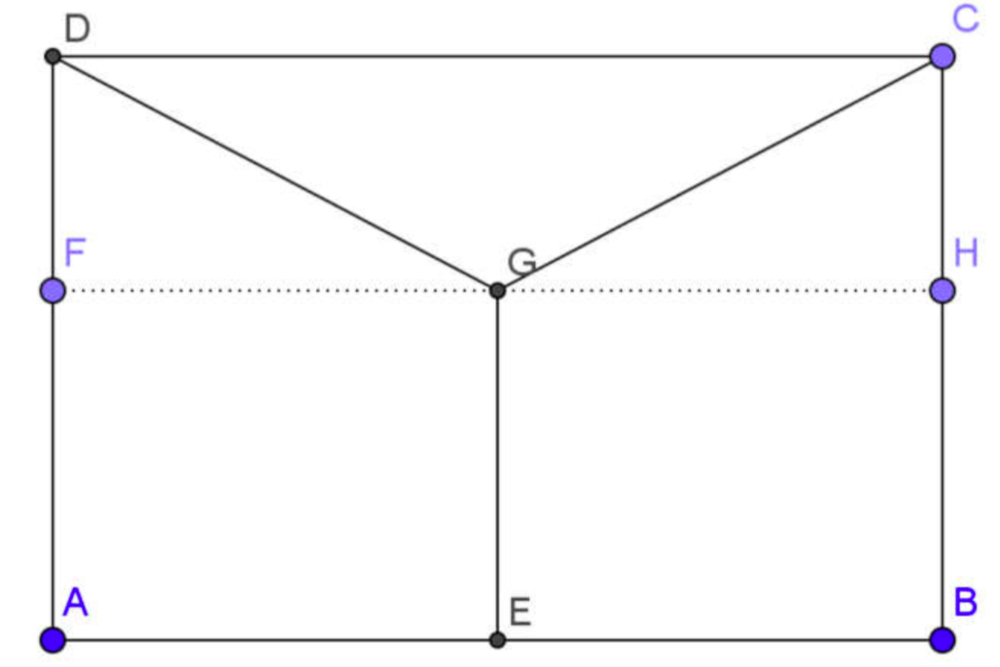
On donne \(\text{AD}=4\) , \(\text{BE}=\text{GH}=6\) . On pose \(\text{DF}=x\).

1. Exprimer en fonction de \(x\)  la somme des longueurs \(\text{DG}+\text{CG}+\text{GE}\) .

2. À l'aide de la partie A, déterminer la valeur de \(x\)  pour laquelle la longueur de canalisation est minimale.

3. Déterminer dans ce cas la valeur de l'angle \(\widehat {\text{HCG}}\).

Partie A

1. \(\lim\limits_{x\rightarrow -\infty }x^2+36=+\infty\)  et \(\lim\limits_{t\rightarrow +\infty }\sqrt t=+\infty\) , par composée on a donc \(\lim\limits_{x\rightarrow -\infty }\sqrt{x^2+36}=+\infty\) , comme \(\lim\limits_{x\rightarrow -\infty}-x=+\infty\) , on a, par somme \(\lim\limits_{x\rightarrow -\infty }f(x)=+\infty\) .

2. \(x^2+36\geqslant x^2 \Rightarrow \sqrt{x^2+36}\geqslant \sqrt{x^2}\)

   \(\Rightarrow\) \(\sqrt{x^2+36}\geqslant x\) pour \(x>0\)

   \(\Rightarrow\) \(2\sqrt{x^2+36}-x\geqslant 2x-x\)

   \(\Rightarrow\) \(f(x)\geqslant x\)

   On a \(\lim\limits_{x\rightarrow +\infty }x=+\infty\)  D'après le théorème de comparaison, on a donc \(\lim\limits_{x\rightarrow+\infty }f(x)=+\infty\) .

3. On a  \(x \mapsto x^2+36\)  est dérivable et positive strictement, donc \(f\)  est dérivable pour \(x \in \mathbb{R}\).

   Pour tout \(x{\in} \mathbb{R}\), \(f'(x)=2\dfrac{2x}{2\sqrt{x^2+36}}-1\) , soit \(f'(x)=\dfrac{2x}{\sqrt{x^2+36}}-1\) .

   \(\sqrt{x^2+36}\)  étant positif, on a \(\dfrac{2x}{\sqrt{x^2+36}}\)  du signe de \(x\)  et si \(x\leqslant 0\) , on a \(\dfrac{2x}{\sqrt{x^2+36}}\leqslant 0\)  d'où \(\dfrac{2x}{\sqrt{x^2+36}}-1<0\) . Soit \(f'(x)<0\) .

4. \(f'(x)=\dfrac{2x}{\sqrt{x^2+36}}-\dfrac{\sqrt{x^2+36}}{\sqrt{x^2+36}}\)   \(\Rightarrow f'(x)=\dfrac{2x-\sqrt{x^2+36}}{\sqrt{x^2+36}}\)   \(\Rightarrow f'(x)=\dfrac{4x^2-(x^2+36)}{(2x+\sqrt{x^2+36})\sqrt{x^2+36}}\)

   \(f'(x)=\dfrac{3x^2-36}{(2x+\sqrt{x^2+36})\sqrt{x^2+36}}\)

   Le dénominateur de cette dernière forme étant positif, on a \(f'(x)\) du signe de \(3x^2-36\)  donc du signe de \(x^2-12=(x-2\sqrt 3)(x+2\sqrt 3)\)

   Sur \(\mathbb{R}^+\), cette quantité est du signe de \(x-2\sqrt 3\) .

5. On obtient alors le tableau des variations de \(f\) :

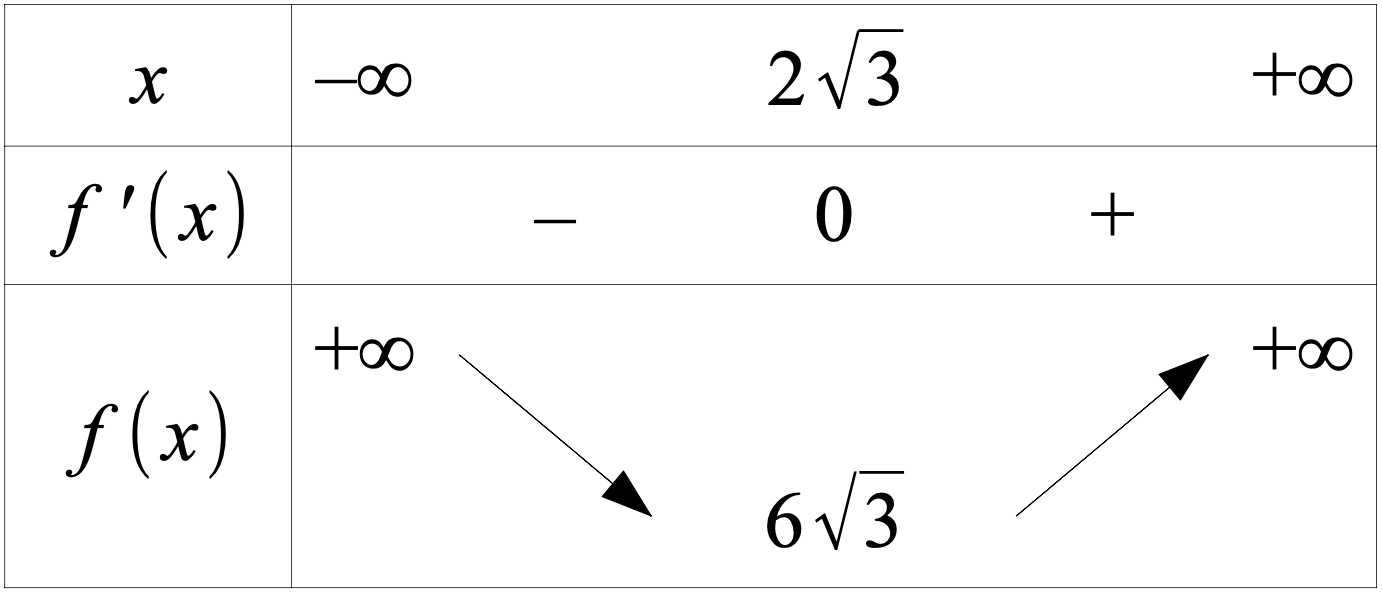
Partie B

1. Dans le triangle DFG rectangle en G, d'après le théorème de Pythagore, \(\text{DG}=\text{CG}=\sqrt{x^2+36}\) .

   D'autre part, \(\text{GE}=4-x\)

   D'où \(\text{DG}+\text{CG}+\text{GE}=2\times \sqrt{x^2+36}+4-x=f(x)+4\) .

2. D'après la partie A, \(f(x)\)  est minimale pour \(x=2\sqrt 3\) .

3. \(\text{HCG}\)  est rectangle en \(\text H\) , d'où \(\widehat {\text{HCG}}=\text{cos}^{-1}\left(\dfrac{\text{HC}}{\text{CG}}\right)=\text{cos}^{-1}\left(\dfrac{\sqrt{12}}{\sqrt{48}}\right)\)

   Donc \(\widehat {\text{HCG}}=\text{cos}^{-1}\left(\sqrt{\dfrac 1 4}\right)\). Soit \(\widehat {\text{HCG}}=\text{cos}^{-1}\left(\dfrac 1 2\right)=\dfrac{\pi} 3\).