SujetCorrigé

le barème est donné à titre indicatif

La calculatrice est autorisée

2 heures

Sujet construit avec David M.

Exercice 1 – 1,5 points - Vrai ou faux ?

Chaque réponse devra être justifiée.

1. Une suite positive majorée est bornée
2. Une suite géométrique de raison \(-2\) est majorée
3. Une suite arithmétique de raison \(3\) est minorée

Exercice 2 – 4 points

On pose \(\text S_n=1^3+2^3+3^3+...+n^3\) avec \(n \geqslant 1\) ;

\(\text S_n\) représente donc la somme des \(n\) premiers cubes des entiers naturels.

1. Calculer : \(\text S_1\), \(\text S_2\), \(\text S_3\) et \(\text S_4\)

2. Exprimer \(\text S_{n+1}\) en fonction de \(\text S_{n}\)

3. Développer et réduire \((n+1)^3\)

4. Démontrer par récurrence que pour tout \(n \geqslant 1\), \(\text S_n=\frac{n^2\times (n+1)^2} 4\)

Exercice 3 – 7 points – D’après Bac Liban 2013

On considère la suite définie sur \(\mathbb{N}\) par \(u_0 = 1\) et \(u_{n+1}=\frac 9{6-u_n}\)

1. A l’aide de votre calculatrice, recopier et compléter le tableau suivant

   \(n\)	0	1	2	3	4	5	6	7	8
   \(u_{n}\)	1	1.800	2.143

2. Quelle conjecture peut-on formuler concernant la suite  ?

3. a. Démontrer par récurrence que, pour tout entier naturel \(n\), \(0<u_n<3\).

   b. Démontrer que, pour tout entier naturel n, \(u_{n+1}-u_n=\frac{(3-u_n)^2}{6-u_n}\)

   c. En déduire une validation de la conjecture formulée à la question 2)

   On désigne par \((v_n)\) la suite définie sur \(\mathbb{N}\) par \(v_n=\frac 1{u_n-3}\)

4. a. Démontrer que la suite \((v_n)\) est une suite arithmétique de raison \(-\frac 1 3\)

   b. En déduire \(v_n\), puis \(u_n\), en fonction de \(n\).

   c. Calculer \(u_8\) à l’aide de la formule trouvée au 4.b. et comparer au résultat trouvé au 1.

Exercice 4 – 5,5 points

On considère la suite \((u_n)\) définie sur \(\mathbb{N}\) par \(0<u_0<1\) et \(u_{n+1}=u_n(2-u_n)\)

Soit \(f\) la fonction définie sur \([0;1]\) par \(f(x)=x(2-x)\).

1. a. On a tracé la courbe représentative de \(f\) sur le graphique ci-dessous ; représenter graphiquement, sans les calculer, les 4 premiers termes de la suite (on pourra prendre, à titre d’exemple, \(u_0=0.3\)).

   

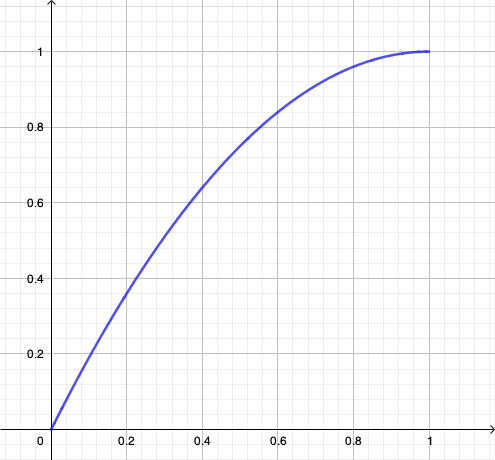
   b. Quelle conjecture peut-on formuler concernant les variations de la suite \((u_n)\)?

2. Etudier sur \([0;1]\) les variations de \(f\)

3. Démontrer que pour tout entier naturel n, \(0<u_n<1\).

4. Démontrer la conjecture de la question 1.b.

Exercice 5 – 2 points

Démontrer par récurrence que la somme des angles dans un polygone non croisé à \(n\) côtés vaut \((n−2)\pi\) radians.

Exercice 1

1. Si une suite est positive, alors elle est minorée par \(0\). La suite est donc à la fois minorée et majorée : Elle est bien bornée. La proposition est VRAIE.

2. Soit la suite géométrique de terme général \(u_n=(-2)^n\) . Pour \(n\) pair, on a \(u_n=4^{\frac n 2}\), quelque soit la valeur \(A\) que l’on pourra choisir, il existera toujours un rang \(n_0\) tel que pour tout \(n>n_0\), \(4^{\frac n 2}>\text A\). Cela signifie qu’aucune valeur A ne peut majorer \((u_n)\). La proposition est FAUSSE.

3. Si \((u_n)\) est une suite arithmétique de raison \(3\), alors \(u_{n+1}-u_n=3\). La suite \((u_n)\) est donc croissante, ce qui implique qu’elle est minorée par son premier terme. La proposition est VRAIE.

Exercice 2

1. On a \(\text S_1=1^3=1\), \(\text S_2=1^3+2^3=9\) , \(\text S_3=1^3+2^3+3^3=36\) , \(\text S_4=\text S_3+4^3=100\) .

2. On a \(\text S_{n+1}=\text S_n+(n+1)^3\) .

3. \((n+1)^3=(n+1)^2\times (n+1)=(n^2+2n+1)\times (n+1)=n^3+3n^2+3n+1\)

4. Soit : \(\text H_n\) : \(1+2^3+3^3+\ldots +n^3=\frac{n^2(n+1)^2} 4\).

   Initialisation

   On a, pour \(n=1\) : \(\frac{1^2(1+1)^2} 4=\frac 4 4=1\) et \(\text S_1=1\) donc \(\text H_1\) est vraie.

   Hérédité

   Supposons \(\text H_n\) vraie pour un rang donné, et montrons qu’alors \(\text H_{n+1}\) est vraie.

   \(\text H_n \Rightarrow 1+2^3+3^3+\ldots +n^3=\frac{n^2(n+1)^2} 4\)

   \(\Rightarrow 1+2^3+3^3+\ldots +n^3+(n+1)^3=\frac{n^2(n+1)^2} 4+(n+1)^3\)

   \(\Rightarrow 1+2^3+3^3+\ldots +(n+1)^3=\frac{n^2(n+1)^2} 4+\frac{4(n+1)^3} 4\)

   \(\Rightarrow 1+2^3+3^3+\ldots +(n+1)^3=\frac{(n+1)^2} 4(n^2+4(n+1))\)

   \(\Rightarrow 1+2^3+3^3+\ldots +(n+1)^3=\frac{(n+1)^2} 4(n+2)^2\)

   \(\Rightarrow 1+2^3+3^3+\ldots +(n+1)^3=\frac{(n+1)^2(n+2)^2} 4\)

   \(\Rightarrow \text H_{n+1}\)

   Conclusion

   On a \(\text H_1\) vraie et \(\text H\) héréditaire, donc, par récurrence sur \(n\), \(\text H_n\) est vraie pour tout \(n \in \mathbb{N}^*\).

Exercice 3

1. Tableau de valeurs

   \(n\)	0	1	2	3	4	5	6	7	8
   \(u_{n}\)	1	1.800	2.143	2.333	2.454	2.538	2.600	2.647	2.684

2. Il semble que la suite \((u_n)\) est croissante.

3. a.

   Soit \(\text P_n\) : \(0<u_n<3\)

   Initialisation

   On a \(u_0=1\) et \(0<1<3\), on a donc \(\text P_0\) vraie.

   Hérédité

   Supposons que \(\text P_n\) est vraie pour un rang \(n\) donné, et montrons qu’alors \(\text P_{n+1}\) est vraie.

   \(\text P_n \Rightarrow 0<u_n<3 \Rightarrow 0>-u_n>-3 \Rightarrow 6>6-u_n>3 \Rightarrow \frac 1 6<\frac 1{6-u_n}<\frac 1 3 \Rightarrow \frac 9 6<\frac 9{6-u_n}<\frac 9 3 \Rightarrow \frac 3 2<u_{n+1}<3 \Rightarrow 0<u_{n+1}<3 \Rightarrow \text P_{n+1}\) .

   Conclusion

   On a \(\text P_0\) vraie et \(\text P\) héréditaire, donc, par récurrence sur \(n\), \(\text P_n\) est vraie pour tout \(n {\in}\mathbb{N}\).

   b. \(u_{n+1}-u_n=\frac 9{6-u_n}-u_n=\frac 9{6-u_n}-\frac{u_n(6-u_n)}{6-u_n}=\frac{u_n^2-6u_n+9}{6-u_n}=\frac{(u_n-3)^2}{6-u_n}\) (identité remarquable)

   c. On a \(0<u_n<3 \Rightarrow 0>-u_n>-3 \Rightarrow 6>6-u_n>3\), soit \(6-u_n>0\) et \((u_n-3)^2\geqslant 0\), par quotient, on a donc \(\frac{(u_n-3)^2}{6-u_n}\geqslant 0\) d’où \(u_{n+1}-u_n\geqslant 0\) et \((u_n)\) est bien croissante.

4. a. On calcule: \(v_{n+1}=\frac 1{u_{n+1}-3}=\frac 1{\frac 9{6-u_n}-3} =\frac{6-u_n}{9-3(6-u_n)}=\frac{6-u_n}{3u_n-9}\) .

   D’où \(v_{n+1}-v_n=\frac{6-u_n}{3(u_n-3)}-\frac 1{u_n-3}=\frac{6-u_n-3}{3(u_n-3)}=-\frac 1 3\). \((v_n)\) est bien une suite arithmétique de raison \(-\frac 1 3\).

   b. On a \(v_0=\frac 1{u_0-3}=-\frac 1 2\). \((v_n)\) a donc pour terme général \(v_n=v_0-\frac 1 3n=-\frac 1 2-\frac n 3\)

   \(v_n=\frac 1{u_n-3} \Rightarrow u_n-3=\frac 1{v_n} \Rightarrow u_n=\frac 1{v_n}+3=-\frac 1{\frac 1 2+\frac n 3}+3=3-\frac 6{3+2n}\)

   c. On calcule \(u_8=3-\frac 6{19}{\approx}2.684\), la valeur approchée est bien correcte.

Exercice 4

1. a. Graphique

   

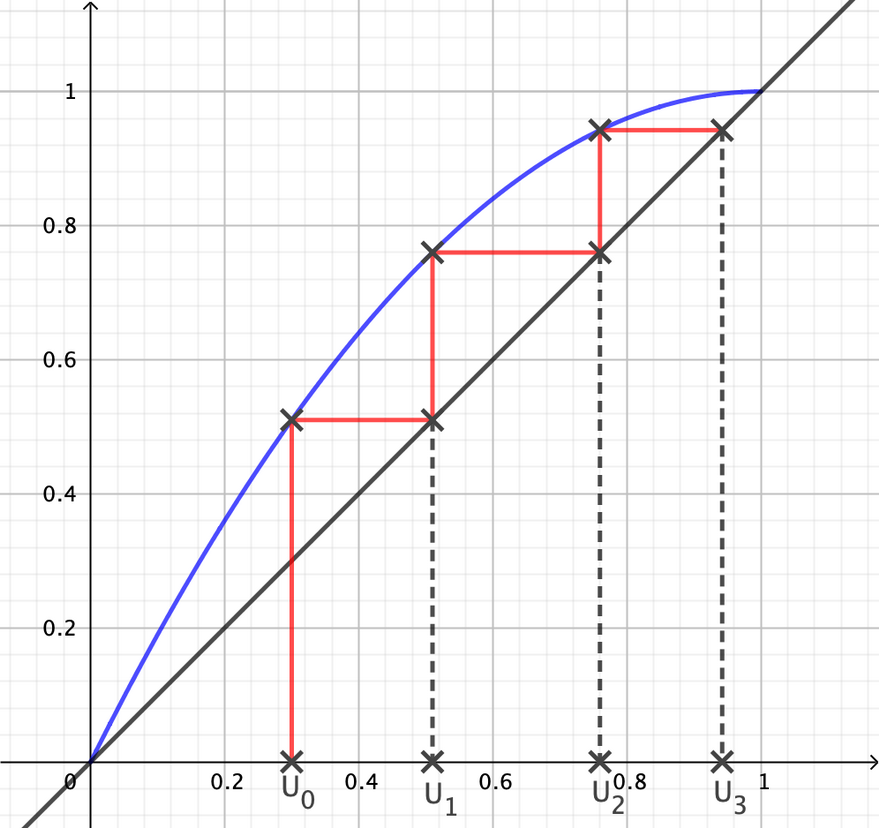
   b. Il semble que la suite \((u_n)\) est croissante.

2. on a \(f(x)=x(2-x)=2x-x^2\).

   \(f\) est une fonction polynomiale, donc dérivable sur \([0\mathrm ;1]\). \(f'(x)=2-2x=2(1-x)\)

   Pour \(x\in [0\mathrm ;1]\), on a \(1-x\geqslant 0\) donc \(f'(x)\geqslant 0 \Rightarrow f\) est croissante sur \([0\mathrm ;1]\).

3. Soit \(\text H_n : 0<u_n<1\) :

Initialisation

\(u_0\in ]0\mathrm ;1[ \Rightarrow 0<u_0<1\) et \(\text H_0\) est vraie.

Hérédité

Supposons \(\text H_n\) vraie pour un rang \(n\) donné, et montrons qu’alors \(\text H_{n+1}\) est vraie.

\(\text H_n \Rightarrow 0<u_n<1 \Rightarrow f(0)<f(u_n)<f(1)\) (car \(f\) croissante) \(\Rightarrow 0<u_{n+1}<1 \Rightarrow \text H_{n+1}\)

Conclusion

\(\text H_0\) est vraie et \(\text H\) est héréditaire, par récurrence sur \(n\), on a donc montré que \(0\leqslant u_n\leqslant 1\) pour tout \(\textit{n} {\in}\mathbb{N}\).

1. \(\frac{u_{n+1}}{u_n}=2-u_n\) or \(0<u_n<1 \Rightarrow -1<-u_n<0 \Rightarrow 1<2-u_n<2\) . D'où \(\frac{u_{n+1}}{u_n}\geqslant 1\) et \(u_n>0 \Rightarrow (u_n)\) croissante.

Exercice 5

Pour que le polygone existe, il faut que \(n\geqslant 3\):

Soit \(\text P_n\) : la somme des angles dans un polygone non croisé à \(n\) côtés vaut \((n-2)\pi\) radian.

Initialisation

La somme des angles du triangle vaut \(\pi\) radian, et \((3-2)\pi=\pi\) .

\(\text P_3\) est donc vraie.

Hérédité

Supposons que \(\text P_n\) est vraie pour un rang \(n\) donné, et montrons qu’alors \(\text P_{n+1}\) est vraie.

\(\text P_n \Rightarrow\) la somme des angles dans un polygone non croisé à \(n\) côtés vaut \((n-2)\pi\) radian

Avec un dessin, on s’aperçoit qu’en ajoutant un point, on obtient un polygone à \(n+1\) côtés.

Premier cas

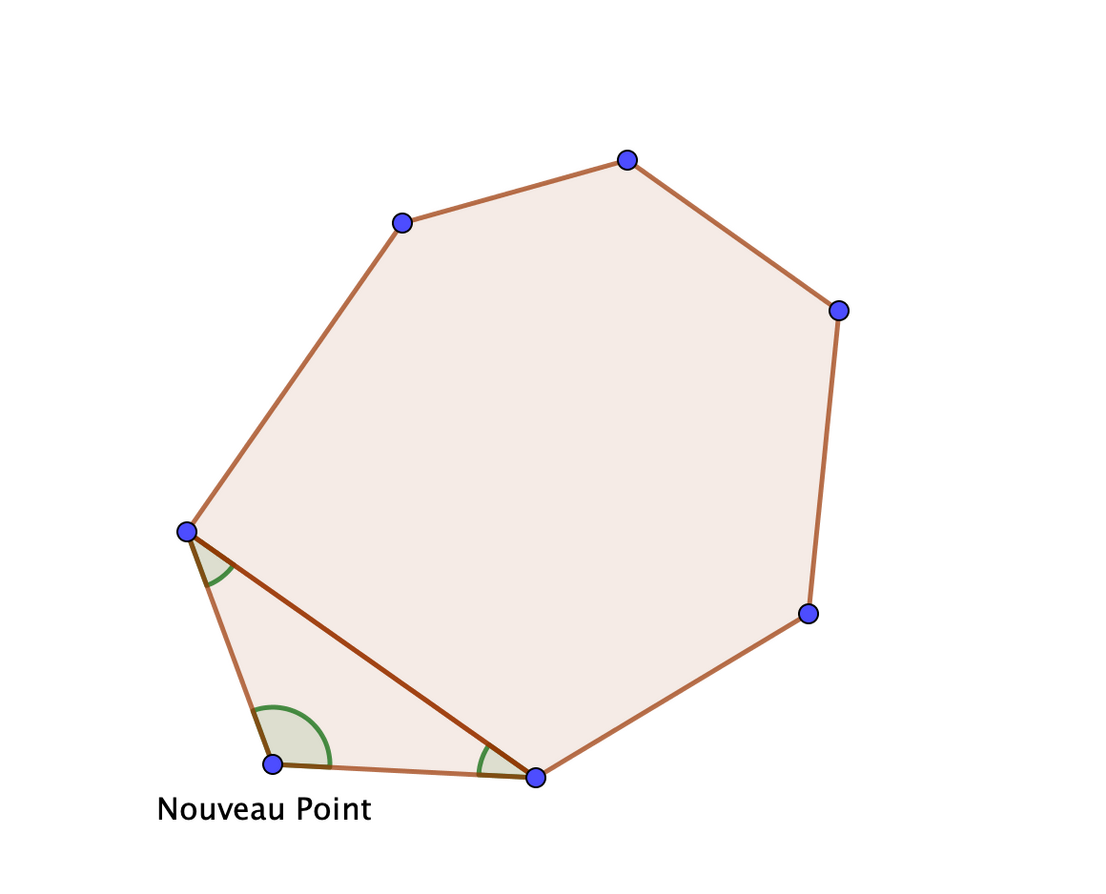
Si le point est à l’extérieur du polygone, on ajoute à la somme des angles la somme des angles d’un triangle (notés en vert) donc \(\pi\).

La somme des angles du polygone à \(n+1\) côtés est alors: \((n-2)\pi+\pi=(n-1)\pi\).

Deuxième cas Ne pas hésiter à corriger le corrigé

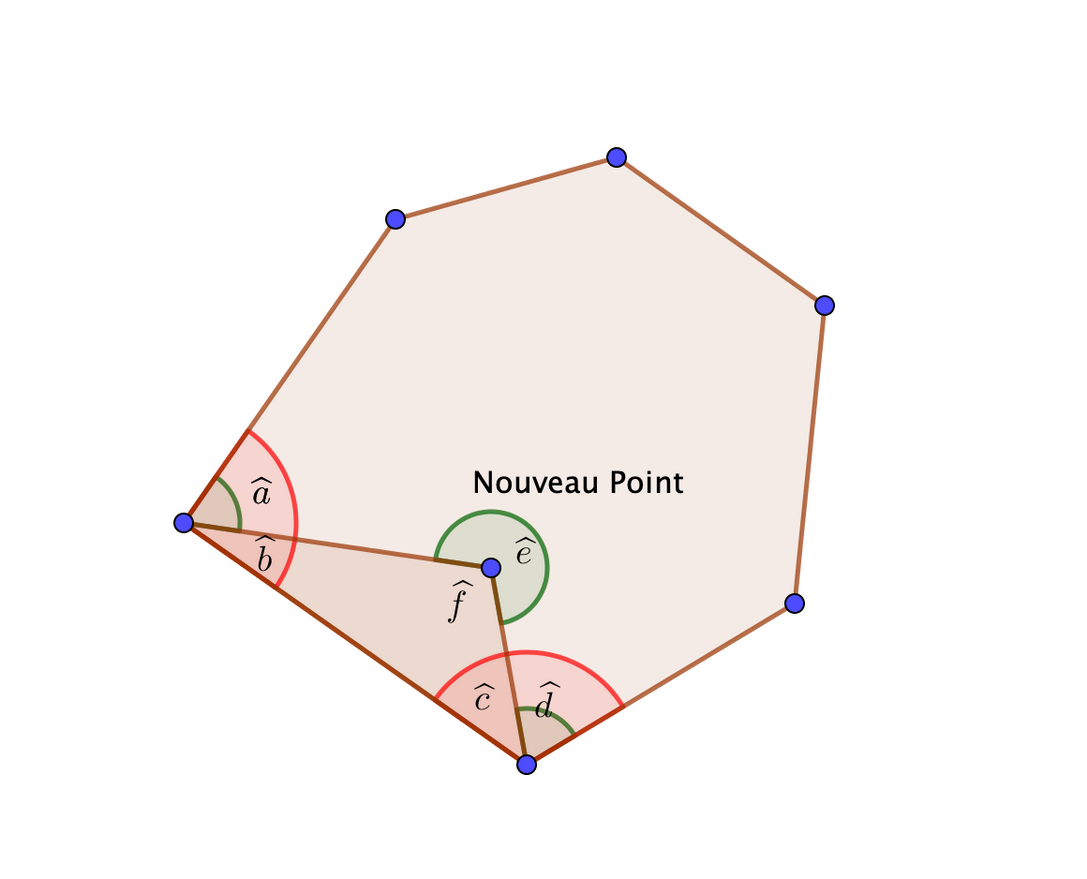
Si le point est à l’intérieur du polygône, on enlève les mesures des angles rouges et on ajoute les mesures des angles verts.

La somme des angles du polygone à \(n+1\) côtés est alors:

\((n-2)\pi-(\widehat a+\widehat b+\widehat c+\widehat d)+\widehat a+\widehat d+\widehat e\) or \(\widehat e=2\pi-\widehat f\)

d'où \((n-2)\pi-(\widehat a+\widehat b+\widehat c+\widehat d)+\widehat a+\widehat d+\widehat e\) = \((n-2)\pi-(\widehat b+\widehat c+\widehat f)+2\pi\)

d’où \((n-2)\pi-(\widehat b+\widehat c+\widehat f)+2\pi\)

or \(\widehat b+\widehat c+\widehat f=\pi\) donc la somme des angles du polygone à \(n+1\) côtés est \((n-2)\pi-\pi+2\pi=(n-1)\pi\).

Dans les deux cas, \(\text P_n \Rightarrow \text P_{n+1}\).

Conclusion

\(\text P_3\) est vraie et \(\text P\) est héréditaire, par récurrence sur \(n\), on a donc montré que la somme des angles dans un polygone non croisé à \(n\) côtés vaut \((n-2)\pi\) radian pour \(n\geqslant 3\).