Ds ln 22 23
-
Déterminer la limite en \(+\infty\) de la fonction:
\[\varphi : x \longmapsto \dfrac{\ln\left(x^2 + 1\right)}{x}\]Corrigé
On a \(\dfrac{\text {ln}(x^2+1)}{x}=\dfrac{\text {ln}\left(x^2\left(1+\dfrac{1}{x^2}\right)\right)}{x}= \dfrac {\text {ln}(x^2)}{x} + \dfrac{\text {ln}\left(1+\dfrac{1}{x^2}\right)}{x}=2 \dfrac {\text {ln}(x)}{x} + \dfrac{\text {ln}\left(1+\dfrac{1}{x^2}\right)}{x}\)
Or, on a \(\lim\limits_{x \to +\infty} \dfrac{\text{ln}(x)}{x}=0\)(cours).
De plus \(\lim\limits_{x \to +\infty} \left(1+\dfrac{1}{x^2}\right)=1\) et, par composée, \(\lim\limits_{X \to 1} \text {ln}(X)=0\), donc, par quotient, \(\lim\limits_{x \to +\infty}\dfrac{\text {ln}\left(1+\dfrac{1}{x^2}\right)}{x}=0\)
Par produit et somme, on obtient donc \(\lim\limits_{x \to +\infty} \dfrac{\text {ln}\left(1+\dfrac{1}{x^2}\right)}{x}=0\)
Soit \(\lim\limits_{x \to +\infty} \dfrac{\ln\left(x^2 + 1\right)}{x}=0\)
-
Soit \(n\) un entier naturel non nul, \(n\) étant fixé pour cette question. On définit la fonction \(f\), sur \([0; +\infty[\) par
\[f_{n}(x) = 2x - 2 + \dfrac{\ln\left(x^2 + 1\right)}{n}\]a. Déterminer la limite de \(f_{n}\) en \(+ \infty\).
b. Calculer la dérivée de \(f_{n}\) sur \([0;+\infty[\).
c. Dresser le tableau de variations de \(f_{n}\).
d. En déduire que l'équation d'inconnue \(x, f_{n}(x) = 0\) admet une unique solution \(\alpha_{n}\) dans \([0;+\infty[\).
e. Justifier que \(0 < \alpha_{n} < 1\).
Corrigé
a. \(\lim\limits_{x \to +\infty} 2x - 2=+\infty\)
\(\lim\limits_{x \to +\infty} x^2+1=+\infty\) donc, par composée, \(\lim\limits_{x \to +\infty} \text {ln}(x^2+1)=+\infty\).
Par quotient, on a donc \(\lim\limits_{x \to +\infty} \dfrac { \text {ln}(x^2+1)}{n}=+\infty\) (car \(n \in \mathbb {N}^*\) est fixé).
Par somme, on obtient donc \(\lim\limits_{x \to +\infty}{f_n(x)}=+\infty\)
b. on a \((ln(u))'=\dfrac{u'}{u}\) , par conséquent:
\(f'_n(x)=2+\dfrac{1}{n}\dfrac{2x}{x^2+1}\)
c. Sur \(\mathbb{R}^+\), on a \(\dfrac{1}{n}\dfrac{2x}{x^2+1} \geq 0 \Rightarrow 2+\dfrac{1}{n}\dfrac{2x}{x^2+1} > 0\)
\(f_n\) est donc strictement croissante sur \(\mathbb{R}^+\).
De plus \(f_n(0)=-2+\dfrac{\text {ln}(1)}0=-2\), on obtient alors le tableau des variations de \(f_n\):
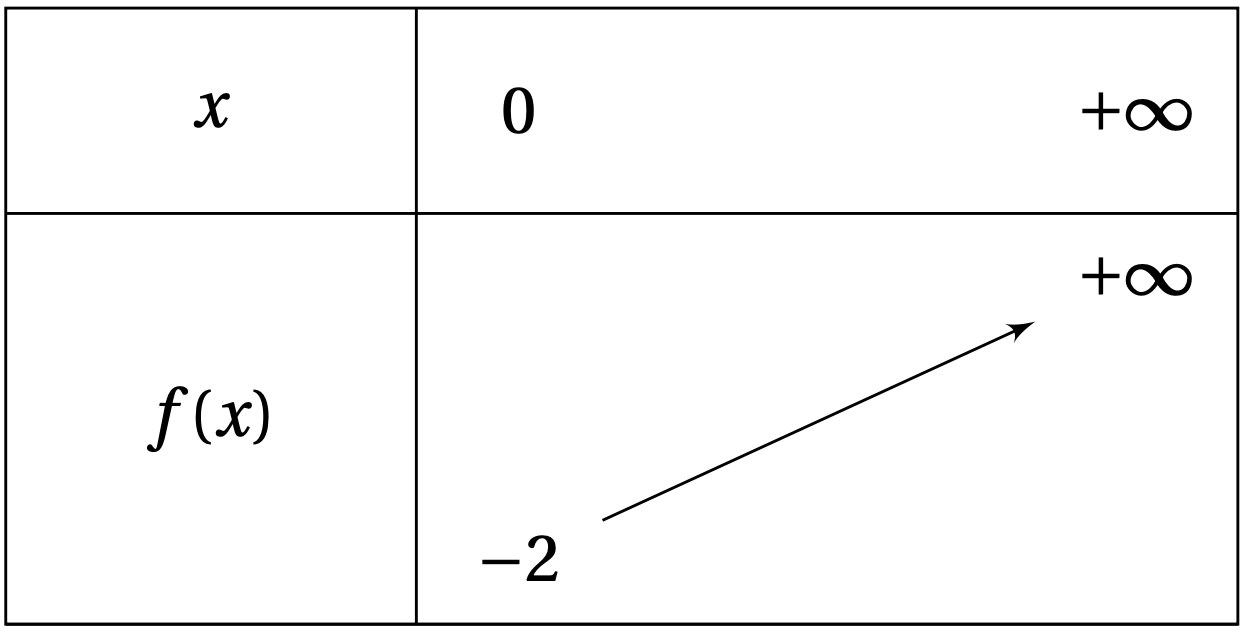
d. Sur \(\mathbb{R}^+\) on a:
-
\(f_n\) continue
-
\(f_n\) strictement croissante
-
\(f_n(0)<0\) et \(\lim\limits_{x \to +\infty}f_n(x)=+\infty\)
D'après le corollaire du théorème sur les valeurs intermédiaires, on a \(f_n(x)=0\) qui admet une unique solution sur \(\mathbb{R}^+\).
e. \(f_n(0)<0\) et \(f_n(1)=\dfrac{\text {ln}(2)}{n}>0\) donc \(0 < \alpha_{n} < 1\)
-
-
Prouver que pour tout entier naturel \(n\) non nul, \(\ln\left({\alpha_{n}}^2 + 1\right) = 2n\left(1 - \alpha_{n}\right)\).
En déduire que \(f_{n+1}\left(\alpha_{n}\right) < 0\).
Corrigé
On a \(f_n(\alpha_n)=0 \Leftrightarrow 2\alpha_n-2+\dfrac{\text {ln}({\alpha_n}^2+1)}{n}=0 \Leftrightarrow \text {ln}({\alpha_n}^2+1)=2n(1-\alpha_n)\)
\(f_{n+1}(\alpha_n)=2\alpha_n-2+\dfrac{\text {ln}({\alpha_n}^2+1)}{n+1}=-2(1-\alpha_n)+\dfrac{2n(1-\alpha_n)}{n+1}=(1-\alpha_n)\left(\dfrac{2n}{n+1}-2\right)=\dfrac{-2}{n+1}(1-\alpha_n)<0\) d'où \(f_{n+1}(\alpha_n)<0\)
-
Étude de la suite \(\left(\alpha_{n}\right)_{n\in\mathbb{N}*}\)
a. À l'aide de la calculatrice, proposer sans justification, des valeurs décimales approchées à \(10^{-2}\) près de \(\alpha_{1}, \alpha_{4}\) et \(\alpha_{10}\).
b. Démontrer que la suite \(\left(\alpha_{n}\right)\) est croissante.
c. En déduire qu'elle est convergente.
d. Déterminer la limite de cette suite.
Dans cette dernière question, toute trace de recherche, même incomplète, ou d'initiative même infructueuse, sera prise en compte dans l'évaluation.
Corrigé
a. Avec la calculatrice on obtient \(\alpha_1 \approx 0.77\), \(\alpha_4 \approx 0.92\) et \(\alpha_{10} \approx 0.97\).
b. On applique le corollaire du théorème sur les valeurs intermédiaires à la fonction \(f_{n+1}\), sur l'intervalle \(]\alpha_n;+\infty[\):
On a \(\lim\limits_{x \to +\infty}f_{n+1}(x)=+\infty\) et \(f_{n+1}(\alpha_n)<0\), \(f_{n+1}\) strictement croissante et continue sur \(]\alpha_n;+\infty[\). Il existe donc une unique valeur \(\alpha_{n+1}\) qui appartient à \(]\alpha_n;+\infty[\) telle que \(f_{n+1}(\alpha_{n+1})=0\) d'où \(\alpha_{n+1}>\alpha_n\) pour \(n \in \mathbb{N}\).
c. \((\alpha_n)\) est croissante et majorée par 1, d'après le théorème de convergence monotone, \((\alpha_n)\) est convergente.
d. Soit \(l=\lim\limits_{n \to +\infty}\alpha_n\).
D'après 3. on a \(\lim\limits_{n \to +\infty}\dfrac{\text {ln}({\alpha_n}^2+1)}{1-\alpha_n}=+\infty\) or \(\lim\limits_{n \to +\infty}\text {ln}({\alpha_n}^2+1)=\text{ln}(l^2+1)\), et cette valeur est une constante strictement positive car \(l>0\).
On a donc \(\lim\limits_{n \to +\infty}\dfrac{\text{ln}(l^2+1)}{1-\alpha_n}=+\infty \Rightarrow\) par inverse, \(\lim\limits_{n \to +\infty}1-\alpha_n=0\), et donc \(\lim\limits_{n \to +\infty}\alpha_n=1\).