Devoir intégration Terminale - Spécialité mathématiques

Durée : 1.25 heure

La calculatrice est autorisée. Une attention particulière sera accordée au soin porté à la rédaction et à la précision des raisonnements.

Les questions sont indépendantes les unes des autres

1. On considère la fonction \(f\)  définie sur \(\mathbb{R}^{+*}\)  par \(f(x)=-4x^3+2x^2+\dfrac{1}{x}\).

   Déterminer la primitive \(\text F\)  de \(f\)  telle que \(\text F(1)=2\).

   Corrigé

   \(f\) est une fonction continue et bien définie sur \(\mathbb{R}^{+*}\)

   On a \(F(x)=-x^4+\dfrac{2}{3}x^3+\ln{x}+C\)

   \(F(1)=-1+\dfrac{2}{3}+0+C=2 \Rightarrow C=\dfrac{7}{3}\)

   On en déduit \(F(x)=-x^4+\dfrac{2}{3}x^3+\ln{x}+\dfrac{7}{3}\)

2. À l'aide de l'image ci-dessous:

   

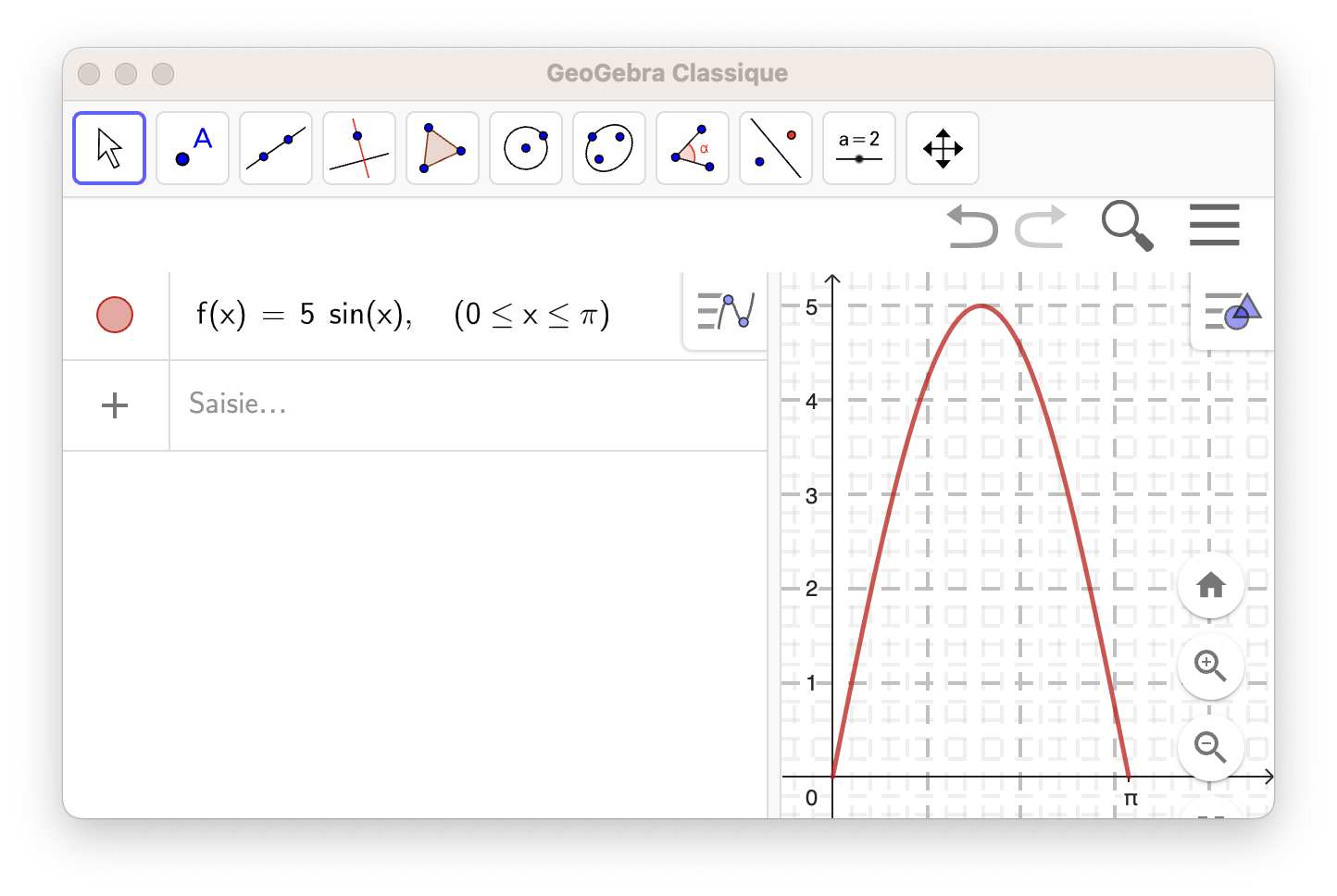
   a. Estimer graphiquement, en unités d'aire, l'aire de la surface \(\text A\)  située entre la courbe, l'axe des abscisses et les deux droites d'équations \(x=0\)  et \(x=\pi\).

   Corrigé

   Il semble que l'aire de la surface est d'environ 9 unités d'aires.

   b. Calculer, en unités d'aire, la valeur exacte de A.

   Corrigé

   On a \(A=\displaystyle\int _0^{\pi}{5\sin x}\text dx=5\displaystyle\int _0^{\pi}{\sin x}\text dx=5 \left[-\cos x \right]_0^{\pi}=5 \times (1-(-1))=10\)

3. Calculer :

   a. \(\text I=\displaystyle\int _0^1\text e^{3t+1}\text dt\)

   Corrigé

   \(t \mapsto \text e^{3t+1}\) est une fonction continue, elle admet donc des primitives.

   \(\text I=\dfrac{1}{3}\displaystyle\int _0^1 3 \text e^{3t+1}\text dt\)

   \(3 \text e^{3t+1}\) est de la forme \(u'\text e^{u}\) avec \(u(t)=3t+1\), cette fonction admet donc \(\text e^u\) comme primitive.

   D'où \(\text I=\dfrac{1}{3} \left[\text e^{3t+1} \right]_0^1=\dfrac{1}{3}\left(\text e^{4}-\text{e} \right)=\dfrac{\text{e}^4-\text{e}}{3}\)

   b. \(\text J=\displaystyle \int _1^2\dfrac{\text e^{\frac{1}{x}}}{x^2}\text dx\)

   Corrigé

   \(x \mapsto \dfrac{\text e^{\frac{1}{x}}}{x^2}\) est une fonction continue sur \([1;2]\), elle admet donc des primitives sur cet intervalle.

   \(\text J=-\displaystyle \int _1^2-\dfrac{1}{x^2}\text e^{\frac{1}{x}}\text dx\)

   \(-\dfrac{1}{x^2}\text e^{\frac{1}{x}}\) est de la forme \(u'\text e^{u}\) avec \(u(x)=\dfrac{1}{x}\)

   D'où \(\text J=-\displaystyle \int _1^2-\dfrac{1}{x^2}\text e^{\frac{1}{x}}\text dx=-\left[\text e^{\frac{1}{x}} \right]_1^2=\left[\text e^{\frac{1}{x}} \right]_2^1=\text{e}-\sqrt{\text{e}}\)

   c. \(\text K=\displaystyle\int _{-1}^1\sin{t}\cos{t}\; \text dt\)

   Corrigé

   La fonction \(t \mapsto \sin{t}\cos{t}\) est une fonction impaire sur l'intervalle centré \([-1;1]\), ceci permet de conclure directement que \(\text K=0\).

   On peut retrouver ce résultat par le calcul:

   \(t \mapsto \sin{t}\cos{t}\) est une fonction continue sur \([-1;1]\), elle admet donc des primitives sur cet intervalle.

   \(\text K=\displaystyle\int _{-1}^1\cos{t}\sin{t}\; \text dt\)

   Or \(\cos{t}\sin{t}\) est de la forme \(u'u\) avec \(u(t)=\sin{t}\)

   D'où \(\text K=\displaystyle\int _{-1}^1\cos{t}\sin{t}\; \text dt=\left[\dfrac{\sin^2{t}}{2} \right]_{-1}^1=\dfrac{1}{2}\left(\sin^2(1)-\sin^2(-1)\right)=0\)

4. On donne \(\text L=\int _1^{\pi}f(x)\text dx=7\). Calculer la valeur moyenne \(\text M\) de la fonction \(f\)  sur l'intervalle \([1\mathrm ;\pi]\).

   Corrigé

   On a \(\text M=\dfrac{1}{\pi-1}\int _1^{\pi}f(x)\text dx=\dfrac{1}{\pi-1}\text L=\dfrac{7}{\pi-1}\)

5. À l'aide d'une intégration par parties, calculer \(\text P=\int _1^2 t^2 \ln{t}\;\text dt\)

   Corrigé

   Soit \(u'(t)=t^2\) et \(v(t)=\ln{t}\) d'où \(u(t)=\dfrac{t^3}{3}\) et \(v'(t)=\dfrac{1}{t}\).

   La formule d'intégration par partie s'écrit: \(\displaystyle\int_a^b u'(t)v(t) \text dt=\left[u(t)v(t)\right]_a^b-\displaystyle\int_a^b u(t)v'(t) \text dt\)

   Soit \(\text P=\left[\dfrac{t^3}{3}\ln{t}\right]_1^2-\displaystyle\int_1^2 \dfrac{t^3}{3}\dfrac{1}{t} \text dt=\dfrac{8}{3}\ln{2}-\displaystyle\int_1^2 \dfrac{t^2}{3} \text dt=\dfrac{8}{3}\ln{2}-\left[\dfrac{t^3}{9}\right]_1^2=\dfrac{8}{3}\ln{2}-\dfrac{7}{9}\)

6. Soit la fonction \(f\) définie sur \([0 ;+\infty [\)  par \(f(x)=\dfrac {x+3}{(x+1)^2(x+2)}\).

   a. Déterminer les nombres \(a\) , \(b\)  et \(c\)  tels que pour tout \(x\geq 0\): \(f(x)= \dfrac a {(x+1)^2}+\dfrac b{x+1}+\dfrac c {x+2}\)

   Corrigé

   Soit l'expression \(\dfrac {x+3}{(x+1)^2(x+2)}=\dfrac a {(x+1)^2}+\dfrac b{x+1}+\dfrac c {x+2}\)

   En la multipliant à gauche et à droite par \((x+1)^2\) et en prenant \(x=-1\), on obtient \(a=2\).

   En la multipliant à gauche et à droite par \((x+2)\) et en prenant \(x=-2\), on obtient \(c=1\).

   En prenant \(x=0\) on obtient \(\dfrac{3}{2}=a+b+\dfrac{c}{2}\) soit \(b=-1\).

   b. En déduire une primitive \(\text F\)  de \(f\)  sur \(\mathbb{R}^+\)

   Corrigé

   On a donc \(f(x)=\dfrac 2 {(x+1)^2}-\dfrac {1}{x+1}+\dfrac 1 {x+2}\)

   Cette fonction est continue sur \(\mathbb{R}^+\), elle admet donc pour primitive: \(F(x)=-\dfrac{2}{x+1}-\ln(x+1)+\ln(x+2)\)

   c. En déduire  \(\text I=\displaystyle\int _0^1f(x)\ \text dx\).

   Corrigé

   \(\text I=\displaystyle\int _0^1f(x)\ \text dx=\left[ F(x)\right]_0^1=-1-\ln{2}+\ln{3}+2-\ln{2}=1-2\ln{2}+\ln{3}\)

7. On considère, pour tout \(n \in \mathbb{N}\), \(\text I_n=\displaystyle \int _0^1x^n\sqrt{1-x} \ \text dx\).

   a. Calculer \(\text I_0\)

   Corrigé

   \(\text I_0=\displaystyle \int _0^1\sqrt{1-x} \; \text dx=\left[- \dfrac{2}{3}(1-x)^{\frac{3}{2}}\right]_0^1=\dfrac{2}{3}\).

   b. À l'aide d'une intégration par parties, montrer que, pour tout \(n \in \mathbb{N}^*\):

   \[\text I_n=\dfrac{2n}{2n+3}I_{n-1}\]
   Corrigé

   Comme on cherche à voir apparaître \(\text I_{n-1}=\displaystyle \int _0^1x^{n-1}\sqrt{1-x} \ \text dx\), on va dériver \(x^n\):

   Soit \(u'(x)=\sqrt{1-x}\) et \(v(x)=x^n\) d'où \(u(x)=- \dfrac{2}{3}(1-x)^{\frac{3}{2}}\) et \(v'(x)=nx^{n-1}\).

   La formule d'intégration par partie s'écrit: \(\displaystyle\int_a^b u'(x)v(x) \text dx=\left[u(x)v(x)\right]_a^b-\displaystyle\int_a^b u(x)v'(x) \text dx\)

   Soit \(\text I_n=\displaystyle\int_0^1 x^n\sqrt{1-x} \text dx=\left[-x^n\dfrac{2}{3}(1-x)^{\frac{3}{2}}\right]_0^1-\displaystyle\int_0^1 -\dfrac{2}{3}(1-x)^{\frac{3}{2}}nx^{n-1} \text dx=0+\dfrac{2n}{3}\displaystyle\int_0^1 (1-x)^{\frac{3}{2}}x^{n-1} \text dx\)

   Et c'est là qu'il ne faut pas abandonner, on va développer:

   \((1-x)^{\frac{3}{2}}x^{n-1}=(1-x)\sqrt{1-x}x^{n-1}=x^{n-1}\sqrt{1-x}-x^{n}\sqrt{1-x}\)

   Ce qui permet de se retrouver en territoire connu:

   Enfin \(\text I_n=\dfrac{2n}{3}\displaystyle\int_0^1\left(x^{n-1}\sqrt{1-x}-x^{n}\sqrt{1-x}\right)\text dx=\dfrac{2n}{3}\left(\displaystyle\int_0^1 x^{n-1}\sqrt{1-x}\text dx - \displaystyle\int_0^1 x^{n}\sqrt{1-x}\text dx\right)=\dfrac{2n}{3}(\text I_{n-1}-\text I_n)\)

   Soit \(I_n=\dfrac{2n}{3}(I_{n-1}-I_n)\) \(\Rightarrow\) \(3I_n=2n(I_{n-1}-I_n)\) \(\Rightarrow\) \((3+2n)I_n=2nI_{n-1}\) d'où \(I_n=\dfrac{2n}{2n+3}I_{n-1}\)

   c. Calculer \(I_1\) et \(I_2\)

   Corrigé

   \(I_1=\dfrac{2}{2+3}I_{0}=\dfrac{4}{15}\) et \(I_2=\dfrac{4}{7}I_{1}=\dfrac{16}{105}\)