Aller au contenu

Devoir Espace et Suites

Le sujet comporte 2 pages dont une annexe Ă  rendre avec la copie.

L'usage de la calculatrice est autorisé. Le barème est donné à titre indicatif.

Un soin particulier sera apporté à la rédaction.

Durée : 1h50

Exercice 1 (7 points)

L’espace est muni d’un repère orthonormé \((O;\vec{i},\vec{j},\vec{k})\)

On considère les points \(A(3 ; 0 ; 1)\), \(B(2 ; 1 ; 2)\) et \(C(-2 ;-5 ; 1)\).

  1. Démontrer que les points \(A\), \(B\) et \(C\) ne sont pas alignés.

  2. On considère le point \(H(0 ;-1 ; 2)\). Montrer que les points \(A\), \(B\), \(C\) et \(H\) sont coplanaires.

  3. Soit \(S(1 ; m-2; 4)\). Déterminer une représentation paramétrique de la droite \((SH)\).

  4. Existe-t-il une valeur de \(m\) pour laquelle le point de coordonnées \((-2;1;-2)\) appartient à la droite ?

  5. Soit le point \(\text{L}\) de coordonnées \((2;3;7)\)

    Existe-t-il une valeur de \(m\) telle que \((SL)\) est parallèle à \((ABC)\) ?

Correction

  1. On calcule \(\overrightarrow{AB} \begin{pmatrix} -1 \\ 1 \\ 1 \end{pmatrix}\) et \(\overrightarrow{AC} \begin{pmatrix} -5 \\ -5 \\ 0 \end{pmatrix}\).

    S'il existe \(k \in \mathbb{R}^*\) tel que \(\overrightarrow{AB}=k\overrightarrow{AC}\) alors \(k\) est forcément nul pour obtenir \(z_{\overrightarrow{AB}}=O\) ce qui est absurde.

    Donc les vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{AC}\) ne sont pas colinéaires et les points \(A\), \(B\) et \(C\) ne sont pas alignés.

  2. Soit \(\overrightarrow{AH} \begin{pmatrix} -3 \\ -1 \\ 1 \end{pmatrix}\).

    Supposons qu'il existe un couple \((x;y) \in \mathbb{R}^2\) tel que \(\overrightarrow{AH}=x \overrightarrow{AB}+y \overrightarrow{AC}\)

    On a alors \(\left\{ \begin{matrix}-3 = -x-5y \\-1 = x-5y \\ 1=x+0y\end{matrix} \right.\)

    D'oĂą \(L_3 \Rightarrow x=1\) et \(L_2 \Rightarrow 5y=x+1 \Rightarrow y=\dfrac{2}{5}\)

    On vérifie que \(L_1\) est vraie pour \(x=1\) et \(y=\dfrac{2}{5} : -x-5y=-1-2=-3\)

    On a donc \(\overrightarrow{AH}= \overrightarrow{AB}+\dfrac{2}{5} \overrightarrow{AC}\). Les points \(A\), \(B\), \(C\) et \(H\) sont bien coplanaires.

  3. On calcule \(\overrightarrow{HS} \begin{pmatrix} 1 \\ m-1 \\ 2\end{pmatrix}\), une représentation paramétrique de \((SH)\) est alors \(\left\{ \begin{matrix}x = t \\y = -1+(m-1)t \\ z=2+2t\end{matrix} \right.\) avec \(t \in \mathbb{R}\)

  4. On résout le système \(\left\{ \begin{matrix}-2 = t \\1 = -1+(m-1)t \\ -2=2+2t\end{matrix} \right.\)

    \(L_1\) donne \(t=-2\), valeur qui vérifie \(L_3\).

    \(L_2\) donne alors une contrainte sur \(m : 1=-1+(m-1) \times (-2)\), soit \(m=0\).

    Pour \(m=0\) le point de coordonnées \((-2;1;-2)\) appartient à la droite \((SH)\).

  5. On calcule \(\overrightarrow{SL} \begin{pmatrix} 1 \\ 5-m \\ 3 \end{pmatrix}\) et on résout \(\overrightarrow{SL}=x \overrightarrow{AB}+y\overrightarrow{AC}\)

    On a alors \(\left\{ \begin{matrix}1 = -x-5y \\5-m = x-5y \\ 3=x+0y\end{matrix} \right.\)

    D'oĂą \(L_3 \Rightarrow x=3\) et \(L_1 \Rightarrow -5y=x+1 \Rightarrow y=-\dfrac{4}{5}\)

    On vérifie que si \(L_2\) est vraie alors \(5-m=3+4\) soit \(m=-2\).

    Pour \(m=-2\), on a bien \((SL)\) est parallèle à \((ABC)\).

Exercice 2 (3 points)

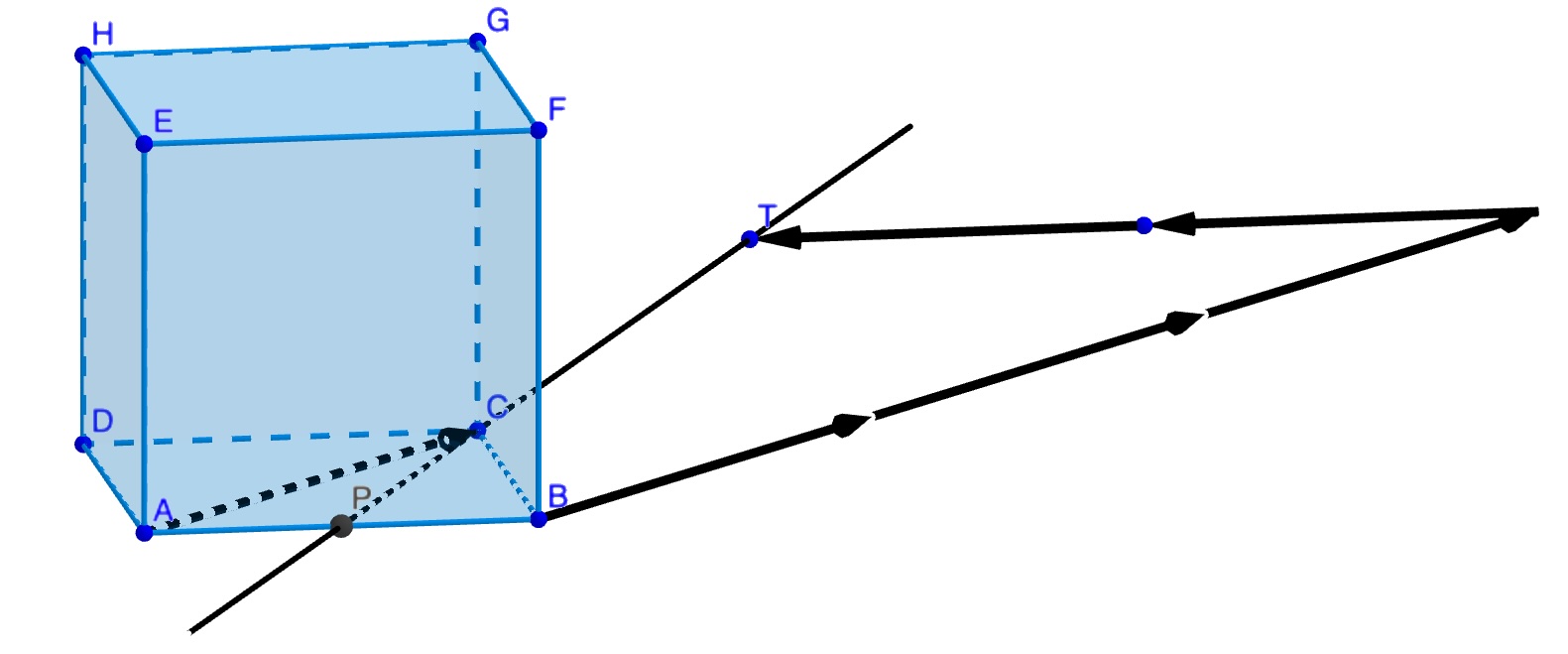
  1. Construire un cube \(\text{ABCDEFGH}\) dont \(\text{ABCD}\) est une face et \(\text{[AE]}\) est une arĂŞte.

  2. Compléter la figure avec les points \(\text{P}\) et \(\text{T}\) tels que \(\overrightarrow{AP}=\dfrac{1}{2}\overrightarrow{AB}\) et \(\overrightarrow{BT}=3\overrightarrow{AC}-2\overrightarrow{AB}\).

  3. Montrer que les points \(\text{C}\), \(\text{T}\) et \(\text{P}\) sont alignés.

Correction

  1. Dessin du cube et construction des points \(P\) et \(T\).

    Construction

  2. On a \(\overrightarrow{PC}=\overrightarrow{PA}+\overrightarrow{AC}=-\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{AC}\) (Chasles)

    \(\overrightarrow{PT}=\overrightarrow{PB}+\overrightarrow{BT}\) (Chasles).

    Soit \(\overrightarrow{PT}=\dfrac{1}{2}\overrightarrow{AB}+3\overrightarrow{AC}-2\overrightarrow{AB}=-\dfrac{3}{2}\overrightarrow{AB}+3\overrightarrow{AC}\)

    Soit \(\overrightarrow{PT}=3\overrightarrow{PC}\).

    Les vecteurs étant colinéaires et le point \(P\) commun, les points \(C\), \(P\) et \(T\) sont alignés.

Exercice 3 (3 points)

Pour chacune des propositions suivantes, dire si elle est vraie ou fausse et justifier la réponse donnée.

Soit \(\left(u_{n}\right)\) la suite définie pour tout \(n \in \mathbb{N}^*\) par \(u_{n} = (-1)^n\).

  1. La suite \(\left(u_{n}\right)\) est bornée.
  2. La suite \(\left(u_{n}\right)\) converge.
  3. La suite de terme général \(\dfrac{u_{n}}{n}\) converge.
  4. Toute suite \(\left(v_{n}\right)\) à termes strictement positifs et décroissante converge vers \(0\).
Correction
  1. \(-1\leqslant u_{n}\leqslant 1\) VRAI
  2. Pour \(n\) pair \(u_{n}=1\) et pour \(n\) impair, \(u_{n}=-1\). Par unicité de la limite, \((u_{n})\) n'est donc pas convergente. FAUX
  3. On a \(-\dfrac1n\leqslant \dfrac{u_{n}}{n}\leqslant \dfrac1n\) et \(\lim\limits_{n \to +\infty}\dfrac{1}{n}=0\), par encadrement, la suite de terme général \(\dfrac{u_{n}}{n}\) admet pour limite 0. VRAI
  4. La suite de terme général \(u_n=\dfrac{1}{2}+\dfrac{1}{n}\) a ses termes strictement positifs et est décroissante mais elle ne converge pas vers \(0\). FAUX

Exercice 4 (7 points)

Soit \(\left(u_{n}\right)\) la suite définie par \(u_{0} = 0,~ u_{1} = 3\) et pour tout nombre entier naturel \(n, u_{n+2} = \dfrac{3}{2}u_{n+1} - \dfrac{1}{2}u_{n}.\)

  1. Calculer \(u_{2}, u_{3}\) et \(u_{4}\).

  2. Montrer que, pour tout nombre entier naturel \(n,~ u_{n+1} = \dfrac{1}{2}u_{n} + 3\).

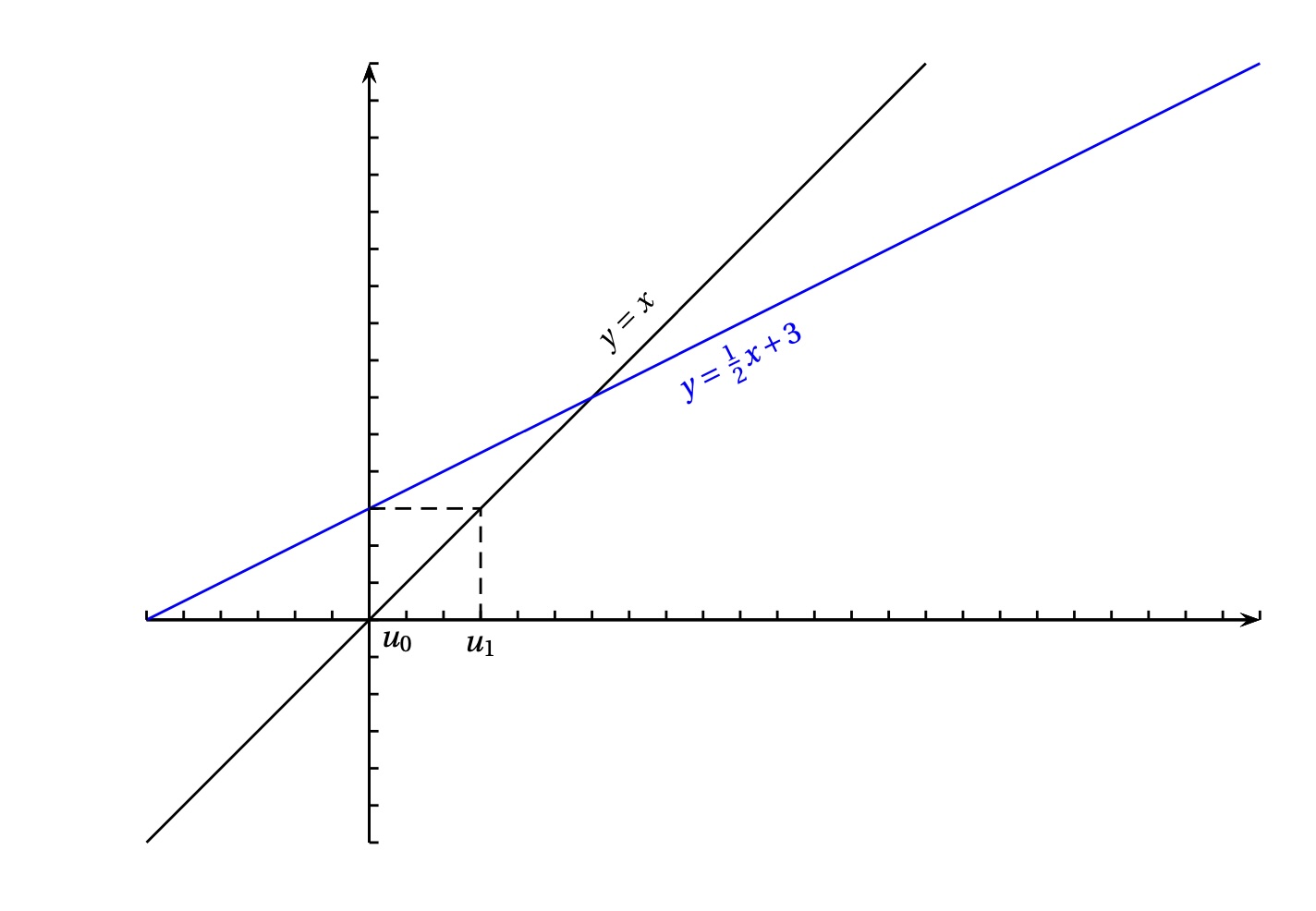
    Sur la figure ci-dessous sont tracées, dans un repère orthonormal, les droites d'équation respectives \(y = x\) et \(y = \dfrac{1}{2}x + 3\).

    Construction

  3. À partir de \(u_{0}\), en utilisant ces deux droites, on a placé \(u_{1}\) sur l'axe des abscisses. De la même manière placer les termes \(u_{2},~u_{3}\) et \(u_{4}\).

    Que peut-on conjecturer sur les variations et la convergence de cette suite ?

  4. Soit \(\left(v_{n}\right)\) la suite définie, pour tout nombre entier naturel \(n\), par \(v_{n} = u_{n} - 6\).

    a. Montrer que la suite \(\left(v_{n}\right)\) est une suite géométrique dont on précisera le premier terme et la raison.

    b. Exprimer \(v_{n}\) puis \(u_{n}\) en fonction de \(n\).

    c. En déduire que la suite \(\left(u_{n}\right)\) est convergente et déterminer sa limite.

Correction

  1. \(u_{2} = \dfrac{3}{2}\times 3 - \dfrac{1}{2} \times 0 = \dfrac{9}{2}\) ;

    \(u_{3} = \dfrac{3}{2}\times \dfrac{9}{2} - \dfrac{1}{2} \times 3 = \dfrac{27}{4} - \dfrac{3}{2} = \dfrac{21}{4}\) ;

    \(u_{4} = \dfrac{3}{2}\times \dfrac{21}{4} - \dfrac{1}{2} \times \dfrac{9}{2} = \dfrac{63}{8} - \dfrac{9}{4} = \dfrac{45}{8}\).

  2. Démonstration par récurrence :

    Initialisation :

    \(u_{1} = 3 = \dfrac{1}{2} \times u_{0} + 3 = \dfrac{1}{2} \times 0 + 3\) est bien vraie ; la relation est vraie au rang \(0\).

    Hérédité :

    Supposons que pour une valeur \(n\) donnée on ait \(u_{n+1} = \dfrac{1}{2}u_{n} + 3.\)

    Or \(u_{n+1} = \dfrac{1}{2}u_{n} + 3 \iff u_{n+1} - 3 = \dfrac{1}{2}u_{n} \iff u_{n} = 2\left(u_{n+1} - 3 \right) \quad (*)\)

    On a par définition : \(u_{n+2} = \dfrac{3}{2}u_{n+1} - \dfrac{1}{2}u_{n} = \dfrac{3}{2}\left(\dfrac{1}{2}u_{n} + 3 \right) - \dfrac{1}{2}u_{n} = \dfrac{1}{4}u_{n} + \dfrac{9}{2}\) ;

    En utilisant la relation (*), on obtient :

    \(u_{n+2} = \dfrac{1}{4}\times 2\left(u_{n+1} - 3 \right) + \dfrac{3}{2} = \dfrac{1}{2}u_{n+1}\).

    La relation est vraie au rang \(n + 1\).

    Conclusion :

    La relation est vraie au rang \(0\) et si elle est vraie au rang \(n\), elle l'est au rang \(n + 1\). On a donc démontré par récurrence que pour tout nombre entier naturel \(n: u_{n+1} = \dfrac{1}{2}u_{n} + 3\).

  3. Construction sur figure.

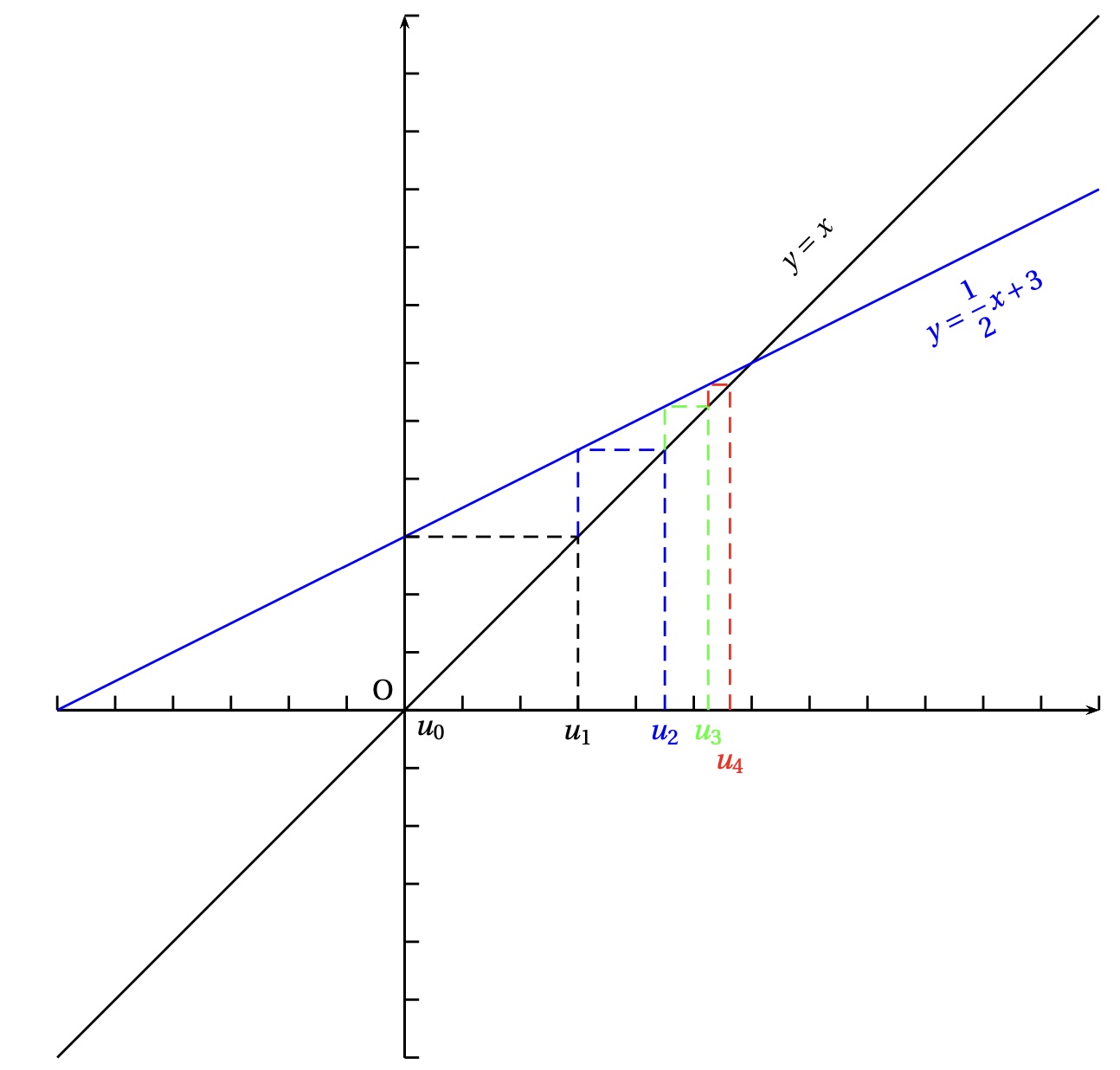
    Construction

    La suite semble être croissante, convergente vers l'ordonnée du point commun aux deux droites c'est-à-dire 6.

  4. Soit \(\left(v_{n}\right)\) la suite définie, pour tout nombre entier naturel \(n\), par \(v_{n} = u_{n} - 6\).

    a. \(v_{n+1} = u_{n+1} - 6 = \dfrac{1}{2}u_{n} + 3 - 6 = \dfrac{1}{2}u_{n} - 3 = \dfrac{1}{2}\left(u_{n} - 6\right) = \dfrac{1}{2}v_{n}\).

    Cette égalité signifie que la suite \(\left(v_{n}\right)\) est géométrique de raison \(\dfrac{1}{2}\) et de premier terme \(v_{0} = u_{0} - 6 = -6\).

    b. On sait que pour \(v_{n} = v_{0}\times \left(\dfrac{1}{2} \right)^n = - \dfrac{6}{2^n}\).

    c. Comme \(-1 < \dfrac{1}{2} < 1,~\lim\limits_{n \to + \infty} v_{n} = 0\). De \(u_{n} = v_{n} + 6\) on en déduit par limite en plus l'infini que \(\lim\limits_{n \to + \infty} u_{n} = 6\).