Devoir in Space

L'usage de la calculatrice n'est pas autorisé.

Un soin particulier sera apporté à la rédaction et aux justifications.

Durée : 60min

Exercice 1

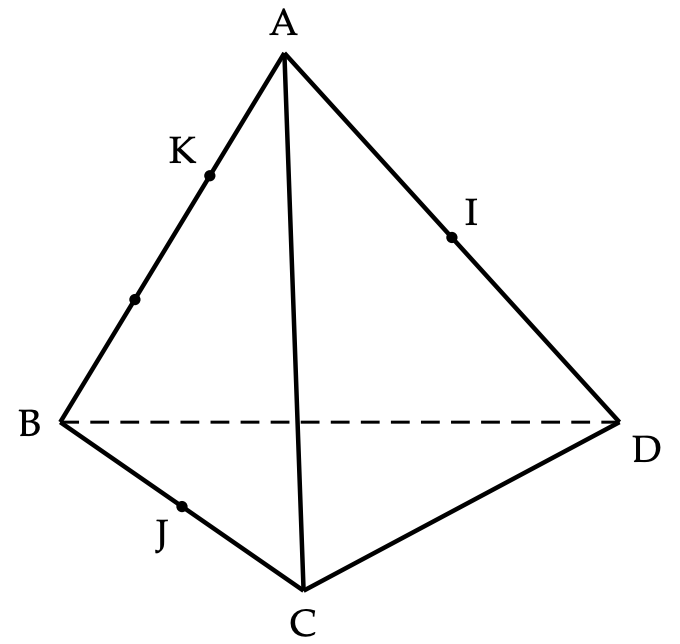
\(\text{ABCD}\)  est un tétraèdre. \(\text I\)  et \(\text J\)  sont les milieux respectifs de \([\text{AD}]\) et \([\text{BC}]\).

\(\text K\)  est le point de l'arête \([\text{AB}]\) tel que \(3\text{AK}=\text{AB}\) .

1. a) Construire le point \(\text M\)  intersection de la droite \((\text{IK})\) et du plan \((\text{BCD})\).

   b) Démontrer que \(\text D\)  est le milieu de \([\text{BM}]\). On appellera \(\text E\)  le milieu de \([\text{BK}]\) et on tracera \([\text{ED}]\).

2. a) En déduire la construction du point \(\text L\)  intersection de \([\text{CD}]\) et du plan \((\text{IJK})\).

   b) Déterminer la valeur de \(k\)  pour laquelle \(\text{CL}=k\times \text{CD}\)

Exercice 2

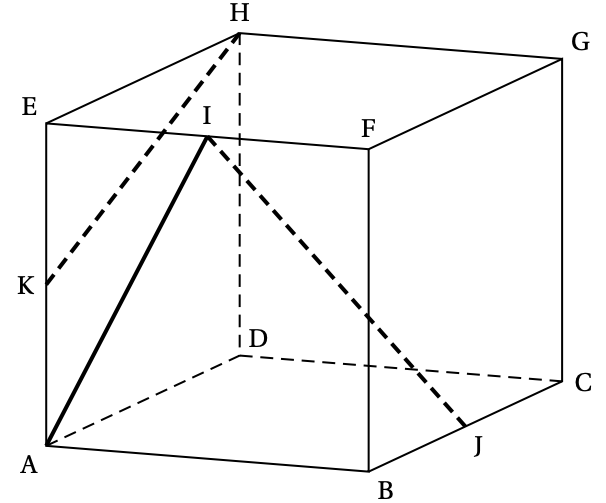
On considère un cube \(\text{ABCDEFGH}\) .

Le point \(\text I\) est le milieu du segment \([\text{EF}]\),

le point \(\text J\)  est le milieu du segment \([\text{BC}]\) 

et le point \(\text K\)  est le milieu du segment \([\text{AE}]\).

1. Les droites \((\text{AI})\) et \((\text{KH})\) sont-elles parallèles ? Justifier votre réponse.

   Dans la suite, on se place dans le repère orthonormé \((\text A;\overrightarrow{\text{AB}},\overrightarrow{\text{AD}},\overrightarrow{\text{AE}})\).

2. a) Donner les coordonnées des points \(\text I\) et \(\text J\) .

   b) Montrer que les vecteurs \(\overrightarrow{\text{IJ}}\) , \(\overrightarrow{\text{AE}}\)  et \(\overrightarrow{\text{AC}}\)  sont coplanaires.

Exercice 3

L'espace est rapporté au repère \((\text O;\vec{i},\vec{j},\vec{k})\).

On considère les points : \(\text A(1;2;-1)\) ,\(\text B(2;-1;3)\) , \(\text C(2;-1;1)\)  et \(\text D(3;-1;1)\) .

Voici des représentations paramétriques des droites \((d)\) et \((d')\) :

\((d)\): \(\left\{\begin{matrix}x=2t+2\\y=-6t-1\\z=8t+3\end{matrix}\right.\) , \(t\in \mathbb{R}\)       \((d')\): \(\left\{\begin{matrix}x=1+k\\y=2-3k\\z=-3+6k\end{matrix}\right.\) , \(k\in \mathbb{R}\)

Pour chacune des cinq affirmations suivantes, indiquer si elle est vraie ou fausse en justifiant la réponse.

1. \(d\) // \((\text{AB})\)

2. \((d')\) est parallèle au plan \((\text{ABC})\)

3. Le point \(\text D\)  est l'image du point \(\text C\)  par la translation de vecteur \(\overrightarrow{\text{AB}}\)

4. \((\text A\mathrm ;\overrightarrow{\text{AB}},\overrightarrow{\text{AC}},\overrightarrow{\text{AD}})\)est un repère de l'espace.

5. Les droites \((d')\) et \((\text{AB})\) sont coplanaires et sécantes.