Exercice donné au bac blanc 2 en 2021-2022

Il s'agit d'un sujet de bac de 2013, largement modifié par mes soins.

SujetCorrigé

Soit $n$  un entier positif. On considère les fonctions $f_n$  définies sur $]0;+\mathrm{\infty }[$ par :

$$f_n(x)={\displaystyle \frac{1+n\text{ln}x}{x^2}}$$

On note ${\text{C}}_n$ les courbes représentatives de $f_n$  dans un repère orthonormé $(\text{O};\overrightarrow{ı},\overrightarrow{ȷ})$ .

PARTIE A Étude d'une fonction particulière

Dans cette partie, on prendra $n=1$

1. Déterminer les limites de la fonction $f_1$  aux bornes de son ensemble de définition.

   Interpréter géométriquement.

2. Étudier les variations de la fonction $f_1$  sur l'intervalle $]0;+\mathrm{\infty }[$ et dresser son tableau de variations.

3. Montrer que l'équation $f_1(x)={\displaystyle \frac{1}{2}}$  admet exactement deux solutions sur $]0;+\mathrm{\infty }[$.

PARTIE B

Dans cette partie, on prendra $n$  quelconque.

1. Calculer $f_{n+1}(x)-f_n(x)$

2. Les courbes ${\text{C}}_n$  ont-elles toutes un point commun ? Si oui, déterminer les coordonnées de ce point.

PARTIE C : Propriété d'une famille de tangentes

1. Déterminer l'équation de la tangente à ${\text{C}}_1$  au point d'abscisse $\text{e}$ . Donner le résultat sous la forme $y=\mathit{ax}+b$  avec $a$  et $b$  sous forme simplifiée.

2. Montrer que les tangentes aux courbes ${\text{C}}_n$  aux points d'abscisse $\text{e}$  ont toutes un point commun que l'on déterminera.

Partie A

1. on a $f_1(x)={\displaystyle \frac{1+\text{ln}x}{x^2}}$ .

   On a $\underset{x\to 0}{lim}\text{ln}x=-\mathrm{\infty }$ et $\underset{x\to 0}{lim}{\displaystyle \frac{1}{x^2}}=+\mathrm{\infty }$, par somme et produit, on a donc $\underset{x\to 0}{lim}{f}_1(x)=-\mathrm{\infty }$.

   ${\text{C}}_1$ admet donc en 0 une asymptote verticale d'équation $x=0$

   On récrit $f_1(x)={\displaystyle \frac{1}{x^2}}+{\displaystyle \frac{\text{ln}x}{x^2}}$ .

   On a $\underset{x\to +\mathrm{\infty }}{lim}{\displaystyle \frac{1}{x^2}}=0$ et $\underset{x\to +\mathrm{\infty }}{lim}{\displaystyle \frac{\text{ln}x}{x^2}}=0$, donc par somme, $\underset{x\to +\mathrm{\infty }}{lim}{f}_1(x)=0$.

   ${\text{C}}_1$ admet donc en $+\mathrm{\infty }$ une asymptote horizontale d'équation $y=0$.

2. $f_1$  est de la forme ${\displaystyle \frac{u}{v}}$  avec $u(x)=1+\text{ln}(x)$  et $v(x)=x^2$  soit $u^{\prime }(x)={\displaystyle \frac{1}{x}}$ et $v^{\prime }(x)=2x$ .

   d'où $f_1^{\prime }(x)={\displaystyle \frac{u^{\prime }(x)v(x)-u(x)v^{\prime }(x)}{(v(x){)}^2}}={\displaystyle \frac{x-(1+\text{ln}(x))\times 2x}{x^4}}={\displaystyle \frac{-x-2x\text{ln}(x)}{x^4}}={\displaystyle \frac{-1-2\text{ln}(x)}{x^3}}$

   $x^3>0$  sur $]0;+\mathrm{\infty }[$ et $-1-2\text{ln}x⩾0\iff -1⩾2\text{ln}(x)\iff {\text{e}}^{-\frac{1}{2}}⩾x$

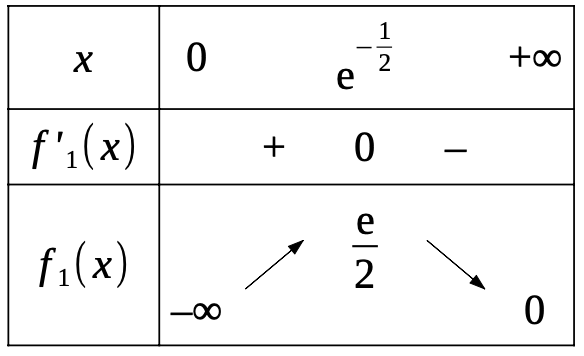
   La fonction $f_1$   est donc croissante sur $\left]0;{\text{e}}^{-\frac{1}{2}}\right]$ et décroissante sur $[{\text{e}}^{-\frac{1}{2}};+\mathrm{\infty }[$.

   on calcule $f_1\left({\text{e}}^{-\frac{1}{2}}\right)=\text{e}\times (1-\frac{1}{2})={\displaystyle \frac{\text{e}}{2}}$ et on obtient alors le tableau des variations de $f_1$ :

   

3. On a $f_1$  strictement croissante et continue sur $\left]0;{\text{e}}^{-\frac{1}{2}}\right]$, de plus $f_1\left({\displaystyle \frac{\text{e}}{2}}\right)>{\displaystyle \frac{1}{2}}$  et $\underset{x\to 0}{lim}{f}_1(x)<{\displaystyle \frac{1}{2}}$ . D'après le corollaire du théorème sur les valeurs intermédiaires, $f_1(x)={\displaystyle \frac{1}{2}}$  admet une unique solution sur l'intervalle $\left]0;{\text{e}}^{-\frac{1}{2}}\right]$ .

   De même sur l'intervalle $[{\text{e}}^{-\frac{1}{2}};+\mathrm{\infty }[$.

   On a donc $f_1(x)={\displaystyle \frac{1}{2}}$  qui a exactement deux solutions sur ${\mathbb{R}}^{+}$.

Partie B

1. $f_{n+1}(x)-f_n(x)={\displaystyle \frac{1+(n+1)\text{ln}x-(1+n\text{ln}x)}{x^2}}={\displaystyle \frac{\text{ln}x}{x^2}}$

2. sur ${\mathbb{R}}^{+}$, on a ${\displaystyle \frac{\text{ln}x}{x^2}}=0$  $\iff$ $\text{ln}(x)=0$  $\iff$ $x=1$ , les courbes ${\text{C}}_n$  passent donc toutes par le même point d'abscisse $1$ .

   On a $f_n(1)={\displaystyle \frac{1+0}{1}}=1$ , ce point a donc pour ordonnée 1. C'est le point de coordonnées $(1;1)$.

Partie C

1. Une équation de la tangente à ${\text{C}}_1$  au point d'abscisse $\text{e}$:

   ${\text{T}}_1$ :  $y=f_1^{\prime }(\text{e})(x-\text{e})+f_1(\text{e})\iff y={\displaystyle \frac{-3}{{\text{e}}^3}}(x-\text{e})+{\displaystyle \frac{2}{{\text{e}}^2}}=-{\displaystyle \frac{3}{{\text{e}}^3}}x+{\displaystyle \frac{5}{{\text{e}}^2}}$

2. Pour déterminer le point commun, on commence par chercher l'intersection de la tangente à ${\text{C}}_0$  en $\text{e}$ , et celle à ${\text{C}}_1$  en $\text{e}$ (dont l'équation vient d'être calculée).

   Équation de la tangente à ${\text{C}}_0$  au point d'abscisse $\text{e}$ :

   ${\text{T}}_0$ : $y=f_0^{\prime }(\text{e})(x-\text{e})+f_0(\text{e})$

   $f_0(x)={\displaystyle \frac{1}{x^2}}$  $\to$ $f_0(\text{e})={\displaystyle \frac{1}{{\text{e}}^2}}$

   $f_0^{\prime }(x)=-{\displaystyle \frac{2}{x^3}}$  $\to$ $f_0^{\prime }(\text{e})=-{\displaystyle \frac{2}{{\text{e}}^3}}$

   D'où ${\text{T}}_0$ :

   $y=-{\displaystyle \frac{2}{{\text{e}}^3}}(x-\text{e})+{\displaystyle \frac{1}{{\text{e}}^2}}=-{\displaystyle \frac{2}{{\text{e}}^3}}x+{\displaystyle \frac{2}{{\text{e}}^2}}+{\displaystyle \frac{1}{{\text{e}}^2}}=-{\displaystyle \frac{2}{{\text{e}}^3}}x+{\displaystyle \frac{3}{{\text{e}}^2}}$

   On peut donc chercher le point d'intersection de ${\text{T}}_0$ et ${\text{T}}_1$ (unique puisque les deux droites ne sont pas parallèles) :

   On résout $-{\displaystyle \frac{2}{{\text{e}}^3}}x+{\displaystyle \frac{3}{{\text{e}}^2}}=-{\displaystyle \frac{3}{{\text{e}}^3}}x+{\displaystyle \frac{5}{{\text{e}}^2}}\iff {\displaystyle \frac{1}{{\text{e}}^3}}x={\displaystyle \frac{2}{{\text{e}}^2}}$ $\iff x=2\text{e}$ et $y=-{\displaystyle \frac{2}{{\text{e}}^3}}\times 2\text{e}+{\displaystyle \frac{3}{{\text{e}}^2}}=-{\displaystyle \frac{1}{{\text{e}}^2}}$, on a donc $(2\text{e};-{\displaystyle \frac{1}{{\text{e}}^2}})$ les coordonnées de ce point d'intersection.

   Reste à vérifier que ce point appartient bien à toutes les tangentes aux courbes ${\text{C}}_n$  en 1.

   On détermine l'équation d'une tangente quelconque :

   $${\text{T}}_n:y=f_n^{\prime }(\text{e})(x-\text{e})+f_n(\text{e})$$

   On calcule :

   $f_n^{\prime }(x)={\displaystyle \frac{{\displaystyle \frac{n}{x}}\times x^2-(1+n\text{ln}x)\times 2x}{x^4}}={\displaystyle \frac{\mathit{xn}-2x-2\mathit{xn}\text{ln}(x)}{x^4}}={\displaystyle \frac{n-2-2n\text{ln}(x)}{x^3}}\Rightarrow f_n^{\prime }(\text{e})={\displaystyle \frac{-2-n}{{\text{e}}^3}}$

   $f_n(\text{e})={\displaystyle \frac{1+n}{{\text{e}}^2}}$ d'où ${\text{T}}_n$  : $y={\displaystyle \frac{-2-n}{{\text{e}}^3}}(x-\text{e})+{\displaystyle \frac{1+n}{{\text{e}}^2}}$

   Pour $x=2\text{e}$ , on obtient $y={\displaystyle \frac{-2-n}{{\text{e}}^2}}+{\displaystyle \frac{1+n}{{\text{e}}^2}}=-{\displaystyle \frac{1}{{\text{e}}^2}}$ .

   Les courbes ${\text{T}}_n$  passent donc toutes par le point de coordonnées $(2\text{e};-{\displaystyle \frac{1}{{\text{e}}^2}})$.