PRODUIT SCALAIRE ET ORTHOGONALITÉ DANS L'ESPACE
1 - REPÈRES ET BASES ORTHONORMÉS DE L'ESPACE
Définition
Un repère \(\left(\text{O};\overrightarrow{\text{OI}},\overrightarrow{\text{OJ}},\overrightarrow{\text{OK}}\right)\) de l'espace est dit orthonormé lorsque les droites \((OI)\), \((OJ)\) et \((OK)\) sont deux à deux perpendiculaires et que \(\text{OI}=\text{OJ}=\text{OK}=1\).
On dit aussi que la base \(\left(\overrightarrow{\text{OI}},\overrightarrow{\text{OJ}},\overrightarrow{\text{OK}}\right)\) est orthonormée.
Un cube dont l'arête mesure une unité de longueur fournit un modèle de repère orthonormé de l'espace.

Remarque
Lorsque le repère \((\text{O};\overrightarrow{\text{OI}},\overrightarrow{\text{OJ}},\overrightarrow{\text{OK}})\) de l'espace est orthonormé, chaque axe est perpendiculaire à toute droite passant par le point \(\text{O}\) et contenu dans le plan défini par les deux autres axes.
Par exemple, la droite \(\text{(OK)}\) est perpendiculaire à toute droite du plan \(\text{(OIJ)}\) passant par \(\text{O}\).
Propriétés
Dans un repère orthonormal \((\text{O};\overrightarrow{\text{OI}},\overrightarrow{\text{OJ}},\overrightarrow{\text{OK}})\),
Si un vecteur \(\overrightarrow{u}\) a pour coordonnées \(\left(\begin{matrix}a \\b \\c\end{matrix}\right)\) alors :
Si les points \(\text{A}\) et \(\text{B}\) ont pour coordonnées respectives \(({x_{A};y_{A};z_{A}})\) et \(({x_{B};y_{B};z_{B}})\), alors :
C'est une extension des propriétés vues dans le plan.
Preuve
On note \(\text{M}\) le point tel que \(\overrightarrow{\text{OM}}=\overrightarrow{u}\).
Les coordonnées de \(\overrightarrow{\text{OM}}\) sont \(\begin{pmatrix} a \\ b \\ c \end{pmatrix}\) et \(\left\| \overrightarrow{u} \right\|^2 = \text{OM}^2\)
Puisque le repère est orthonormal, le triangle \(\text{OM'M}\) est rectangle en \(\text{M'}\).

Donc \(\text{OM'}^2 = a^2 + b^2\) et \(\text{M'M}^2 = \text{OM''}^2 = c^2\)
On en déduit, d'après le théorème de Pythagore que :
\({\parallel \overrightarrow{u} \parallel}^2={\text{OM}}^2={\text{OM'}}^2 + {\text{OM''}}^2=a^2+ b^2 + c^2\), puis \(\parallel \overrightarrow{u} \parallel=\sqrt{a^2 + b^2 + c^2}\)
\(\text{AB}={\parallel \overrightarrow{\text{AB}} \parallel}\) ... : le résultat découle de ce que nous venons de montrer
Exemple : Dans le cube ci-dessus , on a \(P(1;1;0)\) et \(K(0;0;1)\).
On en déduit que \({PK} = \sqrt{(0-1)^2 + (0-1)^2 + (1-0)^2}=\sqrt{3}\)
2 - PRODUIT SCALAIRE DANS L'ESPACE
A - DÉFINITION
Les définitions et propriétés vectorielles concernant le produit scalaire sont valables dans le plan et dans l'espace.
Les démonstrations dans le plan et dans l'espace étant souvent très similaires et la plupart des résultats ayant été vus en classe de Première, ils sont rappelés et étendus à l'espace sans démonstration.
Définition : Formules de polarisation
Soit \(\overrightarrow{u}\) et \(\overrightarrow{v}\) deux vecteurs de l'espace . Le produit scalaire de \(\overrightarrow{u}\) par \(\overrightarrow{v}\) est le nombre réel noté \(\overrightarrow{u} \cdot \overrightarrow{v}\) défini par l'une des formules de polarisation ci-dessous :
\(\overrightarrow{u} \cdot \overrightarrow{v} = \dfrac{1}2\left( \left\| \overrightarrow{u} + \overrightarrow{v} \right\|^2 - \left\| \overrightarrow{u} \right\|^2 - \left\| \overrightarrow{v} \right\|^2 \right)\) ou encore \(\overrightarrow{u} \cdot \overrightarrow{v} = \dfrac{1}{4} \left( \left\| \overrightarrow{u} + \overrightarrow{v} \right\|^2 - \left\| \overrightarrow{u} - \overrightarrow{v} \right\|^2 \right)\)
Remarque
Pour tout vecteur de l'espace, le produit scalaire de \(\overrightarrow{u}\) par lui même, \(\overrightarrow{u} \cdot \overrightarrow{u}\) est appelé carré scalaire de \(\overrightarrow{u}\). On le note \({\overrightarrow{u}}^2\) . On a :
Ce qui donne, pour deux points \(\text{A}\) et \(\text{B}\) :
B - EXPRESSION DU PRODUIT SCALAIRE DANS UN REPÈRE ORTHONORMÉ
Propriété
Soit \(\overrightarrow{u}\) et \(\overrightarrow{v}\) deux vecteurs de l'espace de coordonnées respectives \(\begin{pmatrix} x \\ y \\ z \end{pmatrix}\) et \(\begin{pmatrix} x' \\ y' \\ z' \end{pmatrix}\) dans un repère orthonormé quelconque . On a :
C - PRODUIT SCALAIRE ET COSINUS
Deux vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) de l'espace sont nécessairement coplanaires, c'est à dire qu'il existe \(\text{A}\), \(\text{B}\) et \(\text{C}\) tels que \(\overrightarrow{u}=\overrightarrow{\text{AB}}\) et \(\overrightarrow{v}=\overrightarrow{\text{AC}}\) et (au moins) un plan \(\text{P}\) contenant \(\text{A}\), \(\text{B}\) et \(\text{C}\).
La définition du produit scalaire des vecteurs \(\overrightarrow{\text{AB}}\) et \(\overrightarrow{\text{AC}}\) dans l'espace coïncide avec celle du produit scalaire de ces mêmes vecteurs dans le plan \(\text{P}\) et on en déduit que l'expression du produit scalaire établie avec le cosinus dans le plan est encore valable dans l'espace.
Propriété
Soit \(\overrightarrow{u}\) et \(\overrightarrow{v}\) deux vecteurs non nuls de l'espace et \(\alpha\) la mesure de l'angle géométrique associé à \(\overrightarrow{u}\) et \(\overrightarrow{v}\) . On a :
Remarques
Si \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont colinéaires et de même sens, alors \(\overrightarrow{u} \cdot \overrightarrow{v}=\parallel \overrightarrow{u} \parallel \times \parallel \overrightarrow{v} \parallel\)
Si \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont colinéaires et de sens contraire, alors \(\overrightarrow{u} \cdot \overrightarrow{v}=-\parallel \overrightarrow{u} \parallel \times \parallel \overrightarrow{v} \parallel\)
D - PROJECTION ORTHOGONALE SUR UNE DROITE
Définition
Soit \(\text{d}\) une droite de l'espace.
La projection orthogonale sur la droite \(\text{d}\) est la transformation qui associe à tout point \(\text{M}\) de l'espace le point \(\text{M'}\) intersection de la droite \(\text{d}\) et du plan \(\text{P}\) perpendiculaire à \(\text{d}\) et passant par \(\text{M}\).
\(\text{M'}\) est appelé projeté orthogonal de \(\text{M}\) sur la droite \(\text{d}\).
Une droite est perpendiculaire à un plan si elle est orthogonale à deux droites sécantes de ce plan.
Remarques
Si \(\text{M}\) appartient à la droite \(\text{d}\) , \(\text{M}\) est invariant par la projection orthogonale sur \(\text{d}\). (c'est à dire \(\text{M'}\) et \(\text{M}\) sont confondus)
Si \(\text{M}\) n'appartient pas à la droite \(\text{d}\) , la droite \(\text{d}\) est orthogonale à la droite \((MM')\) qui est incluse dans le plan \(\text{P}\).
\(\text{MM'}\) est la plus courte distance de \(\text{M}\) à un point de \(\text{d}\), on dit que \(\text{MM'}\) est la distance de \(\text{M}\) à la droite \(\text{d}\).
Propriété
Soit \(\text{A}\), \(\text{B}\) et \(\text{M}\) trois points de l'espace tels que \(\text{A}\) et \(\text{B}\) sont distincts.
Si on note \(\text{H}\) le projeté orthogonal de \(\text{M}\) sur la droite \(\text{(AB)}\), alors on a :
Remarques
Dans l'espace, on peut aussi remplacer \(\overrightarrow{\text{AM}}\) par son projeté orthogonal sur un plan qui contient \(\text{(AB)}\).
Si \(\text{M}\) et \(\text{N}\) sont des points de l'espace, et \(\text{H}\) et \(\text{K}\) leurs projetés orthogonaux respectifs sur la droite \(\text{(AB)}\) , alors on a :
E - RÈGLES DE CALCUL
Propriété
Soit \(\overrightarrow{u}\) , \(\overrightarrow{v}\) et \(\overrightarrow{w}\) trois vecteurs de l'espace et \(k\) un réel, on a :
Symétrie:
Bilinéarité:
Remarque
Après quelques calculs, on retrouve des produits scalaires remarquables (bien familiers...)
3 - ORTHOGONALITÉ DANS L'ESPACE
A - DROITES ORTHOGONALES - VECTEURS ORTHOGONAUX
Définition
Deux droites de l'espace sont orthogonales si leurs parallèles menées par un point quelconque de l'espace sont perpendiculaires.
On note : \(\text{d} \perp \text{d'}\)
Deux vecteurs non nuls \(\overrightarrow{u}\) et \(\overrightarrow{v}\) dont les directions sont orthogonales sont dits orthogonaux. On note \(\overrightarrow{u} \perp \overrightarrow{v}\).
Par convention le vecteur nul est orthogonal à tout autre vecteur.
Remarques
-
Si \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont deux vecteurs directeurs de \(\text{d}\) et \(d'\), alors :
\[\text{d} \perp \text{d'} \Leftrightarrow \overrightarrow{u} \perp \overrightarrow{v}\] -
Orthogonal ou perpendiculaire ?
On utilise le mot perpendiculaire quand il y a une intersection non vide, ce qui est forcément le cas entre une droite et un plan, ou entre deux plans.
Il faut être plus prudent dans le cas de deux droites : "perpendiculaire" s'utilise pour les droites orthogonales et sécantes (donc coplanaires). Pour ne prendre aucun risque, on peut utiliser le terme "orthogonal".
Propriété
Soit \(\overrightarrow{u}\) et \(\overrightarrow{v}\) deux vecteurs de l'espace. On a:
Remarques
Pour tout vecteur \(\overrightarrow{u}\) de l'espace, \({\overrightarrow{0}\cdot\overrightarrow{u}}=0\). Le vecteur nul est donc orthogonal à tout vecteur de l'espace.
Conséquences de la définition :
Propriété
Si deux droites sont orthogonales, alors toute droite parallèle à l'une est orthogonale à l'autre.
Si deux droites sont parallèles, alors toute droite orthogonale à l'une est orthogonale à l'autre.
ATTENTION : Certaines règles vraies dans le plan ne sont pas vraies dans l'espace.
Par exemple, dans le plan, deux droites perpendiculaires à une même droite sont parallèles entre elles; ce qui n'est pas vrai dans l'espace.
B - DROITE ORTHOGONALE À UN PLAN
Définition - Propriété
Une droite \(\text{d}\) est orthogonale à un plan \(\text{P}\) si elle est orthogonale à deux droites sécantes \(\text{d}_1\) et \(\text{d}_2\) de ce plan.
Si une droite est orthogonale à un plan, alors elle est orthogonale à toutes les droites de ce plan.

Preuve
"Si une droite est orthogonale à un plan, alors elle est orthogonale à toutes les droites de ce plan."
Soit une droite \(\text{d}\) orthogonale à un plan \(\text{P}\) ; elle est donc orthogonale à deux droites sécantes \(\text{d}_1\) et \(\text{d}_2\) de ce plan.
Soit \(\overrightarrow{v_1}\), \(\overrightarrow{v_2}\) et \(\overrightarrow{u}\) des vecteurs directeurs respectifs de \(\text{d}_1\), \(\text{d}_2\) et \(\text{d}\).
On a \(\text{d}_1 \perp \text{d} \Rightarrow \overrightarrow{v_1} \perp \overrightarrow{u} \Rightarrow {\overrightarrow{v_1}\cdot \overrightarrow{u}}=0\)
Et \(\text{d}_2 \perp \text{d} \Rightarrow \overrightarrow{v_2} \perp \overrightarrow{u} \Rightarrow \overrightarrow{v_2}\cdot\overrightarrow{u}=0\)
Soit \(\Delta\) une droite du plan \(\text{P}\) dirigée par un vecteur directeur \(\overrightarrow{w}\).
\(\text{d}_1\) et \(\text{d}_2\) étant sécantes, les vecteurs \(\overrightarrow{v_1}\) et \(\overrightarrow{v_2}\) sont deux vecteurs directeurs de \(\text{P}\).
Il existe donc deux réels \(a\) et \(b\) tels que \(\overrightarrow{w}=a \overrightarrow{v_1} + b \overrightarrow{v_2}\).
On a alors \(\overrightarrow{w} \cdot \overrightarrow{u}=a \overrightarrow{v_{1}} \cdot \overrightarrow{u} + b \overrightarrow{v_2}\cdot\overrightarrow{u}=0\), ce qui prouve que \(\overrightarrow{w}\) et \(\overrightarrow{u}\) sont orthogonaux et donc que \(\text{d}\) et \(\Delta\) sont orthogonaux.
Propriété
Il existe une unique droite passant par un point donné et orthogonale à un plan donné.

Il existe un unique plan passant par un point donné et orthogonal à une droite donnée.

Si deux droites sont parallèles, alors tout plan orthogonal à l'une est orthogonal à l'autre.
Si deux droites sont orthogonales à un même plan, alors elles sont parallèles.

Si deux plans sont parallèles, alors toute droite orthogonale à l'un est orthogonale à l'autre.
Si deux plans sont orthogonaux à une même droite, alors ils sont parallèles.

Remarques
En fait, il faut retenir que la relation d'orthogonalité ne lie pas seulement une droite et un plan, mais une famille de plans tous parallèles entre eux à une famille de droites toutes parallèles entre elles.
Pour montrer qu'une droite \(\text{d}\) est orthogonale à un plan \(\text{P}\), il suffit de montrer qu'un vecteur directeur de \(\text{d}\) est orthogonal à un couple de vecteurs directeurs de \(\text{P}\).
Un plan \(\text{P}\) est perpendiculaire à un plan \(\text{Q}\) (\(\text{Q} \perp \text{P}\)), s'il existe une droite de \(\text{P}\) orthogonale à \(\text{Q}\).
C - VECTEUR NORMAL À UN PLAN
Définition
Un vecteur normal à un plan \(\text{P}\) est un vecteur non nul dont la direction est orthogonale au plan \(\text{P}\).
Remarques
Si deux vecteurs sont des vecteurs normaux à un même plan \(\text{P}\), alors ils sont colinéaires.
Deux plans de vecteurs normaux orthogonaux sont perpendiculaires.
On peut entièrement définir un plan par la donnée d'un point \(\text{A}\) et d'un vecteur normal \(\overrightarrow{n}\) au plan.
Il s'agit de l'ensemble des points \(\text{M}\) de l'espace telle que \(\overrightarrow{\text{AM}} \cdot \overrightarrow{n}=0\)
4 - ÉQUATION CARTÉSIENNE D'UN PLAN
Propriété
Le plan qui passe par \(\text{A}\) et de vecteur normal \(\overrightarrow{n}\) est l'ensemble des points \(\text{M}\) tels que :
Propriété
Tout plan admet une équation du type \(ax + by + cz + d=0\) où l'un au moins des réels \(a\), \(b\) et \(c\) est non nul et \(d\) est un réel quelconque. De plus, le vecteur non nul \(\overrightarrow{n} \begin{pmatrix}a \\b \\c \end{pmatrix}\) est normal à \(\text{P}\).
Réciproquement :
Soit \(a\), \(b\), \(c\) et \(d\) des réels tels que l'un au moins des réels \(a\), \(b\) et \(c\) n'est pas nul.
L'ensemble des points \(M(x;y;z)\) de l'espace tels que \(ax + by + cz + d=0\) est un plan de vecteur normal \(\overrightarrow{n}{\begin{pmatrix} a \\ b \\ c \end{pmatrix}}\)
Remarques
Si \(a\) , \(b\) et \(c\) sont nuls simultanément, deux cas se présentent :
-
\(d \eq 0\) , et alors la relation \(ax + by + cz + d=0\) est toujours vérifiée
-
\(d \neq 0\) , et alors la relation \(ax + by + cz + d=0\) n'est jamais vérifiée
Preuve : exigible
Soit \(\text{P}\) un plan, \(\overrightarrow{n}{\begin{pmatrix} a \\ b \\ c \end{pmatrix}}\) un vecteur normal à \(\text{P}\) et \(A(x_A;y_A;z_A)\) un point de \(\text{P}\).
Soit \(M(x;y;z)\) un point de l'espace.
On a \(M \in P \Leftrightarrow \overrightarrow{\text{AM}} \cdot \overrightarrow{n}=0 \Leftrightarrow a(x-x_{A}) + b(y-y_{A}) + c(z-z_{A})= 0 \Leftrightarrow ax + by + cz-ax_{A}-by_{A}-cz_{A}=0\)
En posant \(d=-ax_{A}-by_{A}-cz_{A}\), on obtient :
- Réciproquement :
Soit \(a\), \(b\), \(c\) et \(d\) des réels tels que l'un au moins des réels \(a\), \(b\) et \(c\) n'est pas nul.
On considère l'ensemble \(E\) des points \(M(x;y;z)\) de l'espace tels que \(ax + by + cz + d=0\) et on note \(\overrightarrow{n}\) le vecteur de coordonnées \(\begin{pmatrix} a \\ b \\ c \end{pmatrix}\).
On considère, par exemple, que \(a \neq 0\). Le point \(A(-\dfrac{d}{a};0;0)\) est un point de \(E\).
Pour tout point \(M(x;y;z)\) de l'espace, on a \(\overrightarrow{\text{AM}}(x + \dfrac{d}{a};y;z)\).
Ainsi \(\overrightarrow{\text{AM}} \cdot \overrightarrow{n}=ax + by + cz + d=0\)
L'ensemble \(E\) est donc l'ensemble des points \(\text{M}\) tels que \(\overrightarrow{\text{AM}} \cdot \overrightarrow{n}=0\), c'est à dire le plan passant par \(\text{A}\) et de vecteur normal \(\overrightarrow{n}\).
Remarques
-
Un plan admet une infinité d'équations.
Si \(ax + by + cz + d=0\) est l'équation d'un plan, alors \(k(ax + by + cz + d)=0\) , où \(k \in \mathbb{R}^{\text{*}}\) , est aussi une équation de ce plan.
Les équations \(x–y+z–4=0\) et \(\dfrac{x}{4}-\dfrac{y}{4} + \dfrac{z}{4}-1=0\) sont deux équations du même plan.
-
Si \(d \neq 0\), le plan ne passe pas par l'origine du repère. On peut alors toujours choisir une équation de la forme \(a'x + b'y + c'z + 1=0\)
-
Lorsque \(\text{P}\) est un plan parallèle à l'un des plans de coordonnées, il admet comme vecteur normal l'un des vecteurs \(\overrightarrow{i}\) , \(\overrightarrow{j}\) ou \(\overrightarrow{k}\) , et on a alors :
-
tout plan parallèle au plan \(({xOy})\) admet une équation du type \(z=k\)
-
tout plan parallèle au plan \(({yOz})\) admet une équation du type \(x=k\)
-
tout plan parallèle au plan \(({xOz})\) admet une équation du type \(y=k\)
-
5 - POSITIONS RELATIVES, ÉQUATIONS CARTÉSIENNES ET REPRÉSENTATIONS PARAMÉTRIQUES
A - POSITION RELATIVE DE DEUX PLANS
Soit \(P_1\) et \(P_2\) deux plans d'équations respectives \(a_{1}x + b_{1}y + c_{1}z + d_{1}=0\) et \(a_{2}x + b_{2}y + c_{2}z + d_{2}=0\) , et de vecteurs normaux respectifs \(\overrightarrow{n_{1}}\) et \(\overrightarrow{n_{2}}\).
On peut savoir à priori si les deux plans sont sécants ou parallèles selon que leurs vecteurs normaux sont colinéaires ou non.
En particulier, lorsqu'ils sont sécants, pour trouver les coordonnées de leurs points d'intersection, on résout le système formé par leurs deux équations. Ce système possède alors une infinité de solutions qui sont représentées par les points de la droite \(d\), intersection de \(P_1\) et \(P_2\).
Le tableau ci-dessous résume les différentes positions de \(P_1\) et \(P_2\) et indique l'ensemble des solutions du système:
| \(P_1\) et \(P_2\) sont parallèles | \(P_1\) et \(P_2\) sont sécants |
|---|---|
| \(\overrightarrow{n_{1}}\) et \(\overrightarrow{n_{2}}\) colinéaires | \(\overrightarrow{n_{1}}\) et \(\overrightarrow{n_{2}}\) non colinéaires |
| Les plans \(P_1\) et \(P_2\) sont soit confondus, soit strictement parallèles | |
| \((S)\) admet alors une infinité de solutions, tous les triplets \((x;y;z)\) solution de l'une des deux équations ou aucune | \((S)\) admet une infinité de solutions : tous les triplets coordonnées des points de \(d\) |
Remarques :
-
On dit que \((S)\) est un système d'équations cartésiennes de la droite \(d\).
-
La démarche géométrique permet de prévoir à priori le nombre de solutions.
B - POSITION RELATIVE D'UNE DROITE ET D'UN PLAN
Soit \(\text{P}\) le plan d'équation \(ax + by + cz + d=0\) de vecteur normal \(\overrightarrow{n}\left({\begin{matrix} a \\ b \\ c \end{matrix}}\right)\) et \(d\) la droite de vecteur directeur \(\overrightarrow{u}\left({\begin{matrix} \lambda \\ \beta \\ \gamma \end{matrix}}\right)\) et passant par le point \(\text{A}\) de coordonnées \((x_{A};y_{A};z_{A})\).
On peut savoir à priori si \(d\) est sécante ou parallèle à \(\text{P}\) suivant que \(\overrightarrow{n}\) est orthogonal ou non à \(\overrightarrow{u}\). En particulier, si \(d\) coupe \(\text{P}\), leur point d'intersection \(I\) a pour coordonnées \((x;y;z)\) solution du système :
Le tableau ci-dessous résume les différentes positions de \(d\) et \(\text{P}\) et indique l'ensemble des solutions du système \((S)\) .
| \(d\) et \(\text{P}\) sont strictement parallèles | \(d\) incluse dans \(\text{P}\) | \(d\) et \(\text{P}\) sont sécants |
|---|---|---|
| \(\overrightarrow{n} \perp \overrightarrow{u}\) | \(\overrightarrow{n} \perp \overrightarrow{u}\) | \(\overrightarrow{n} \not\perp \overrightarrow{u}\) |
| \((S)\) n'admet aucune solution | \((S)\) admet une infinité de solutions : tous les triplets coordonnées des points de \(d\) | \((S)\) admet une unique solution : \((x_I;y_I;z_I)\) coordonnées de \(I\) |
Remarque :
Si \(d\) est définie comme l'intersection de deux plans \(P_1\) et \(P_2\) , la recherche de l'intersection de \(d\) et \(\text{P}\) peut se ramener à celle des trois plans \(P_1\) , \(P_2\) et \(\text{P}\).
6 - PROJECTION ORTHOGONALE SUR UN PLAN
Définition
Soit \(\text{P}\) un plan de l'espace.
La projection orthogonale sur le plan \(\text{P}\) est la transformation qui associe à tout point \(\text{M}\) de l'espace le point \(\text{M'}\) intersection du plan \(\text{P}\) et de la droite perpendiculaire à \(\text{P}\) passant par \(\text{M}\).
\(\text{M'}\) est appelé projeté orthogonal de \(\text{M}\) sur le plan \(\text{P}\).

Remarques
Si \(\text{M}\) appartient au plan \(\text{P}\) , \(\text{M}\) est invariant par la projection orthogonale sur \(\text{P}\).
Propriété-définition :
Soit \(\text{P}\) un plan de l'espace, \(\text{M}\) un point de l'espace et \(\text{M'}\) son projeté orthogonal sur le plan \(\text{P}\).
\(\text{MM'}\) est la plus courte distance de \(\text{M}\) à un point de \(\text{P}\), On dit que \(\text{MM'}\) est la la distance de \(\text{M}\) au plan \(\text{P}\).
\(\text{M'}\) est le point de \(\text{P}\) le plus proche de \(\text{M}\)
Preuve : exigible
On a vu : "si une droite est orthogonale à un plan, alors elle est orthogonale à toutes les droites de ce plan."
Ainsi, pour tout autre point \(\text{N}\) du plan \(\text{P}\), la droite \(\text{(M'N)}\) est orthogonale à la droite \(\text{(MM')}\) et donc perpendiculaire étant donné que les deux droites ont le point \(\text{M'}\) en commun.
On en déduit que le triangle \(\text{MM'N}\) est rectangle en \(\text{M'}\).
Le côté le plus long d'un triangle rectangle étant l'hypoténuse, on en déduit que \(\text{MM'}<\text{MN}\).
7 - PROJETÉ ORTHOGONAL : APPLICATIONS
A - COORDONNÉES DU PROJETÉ ORTHOGONAL D'UN POINT SUR UN PLAN
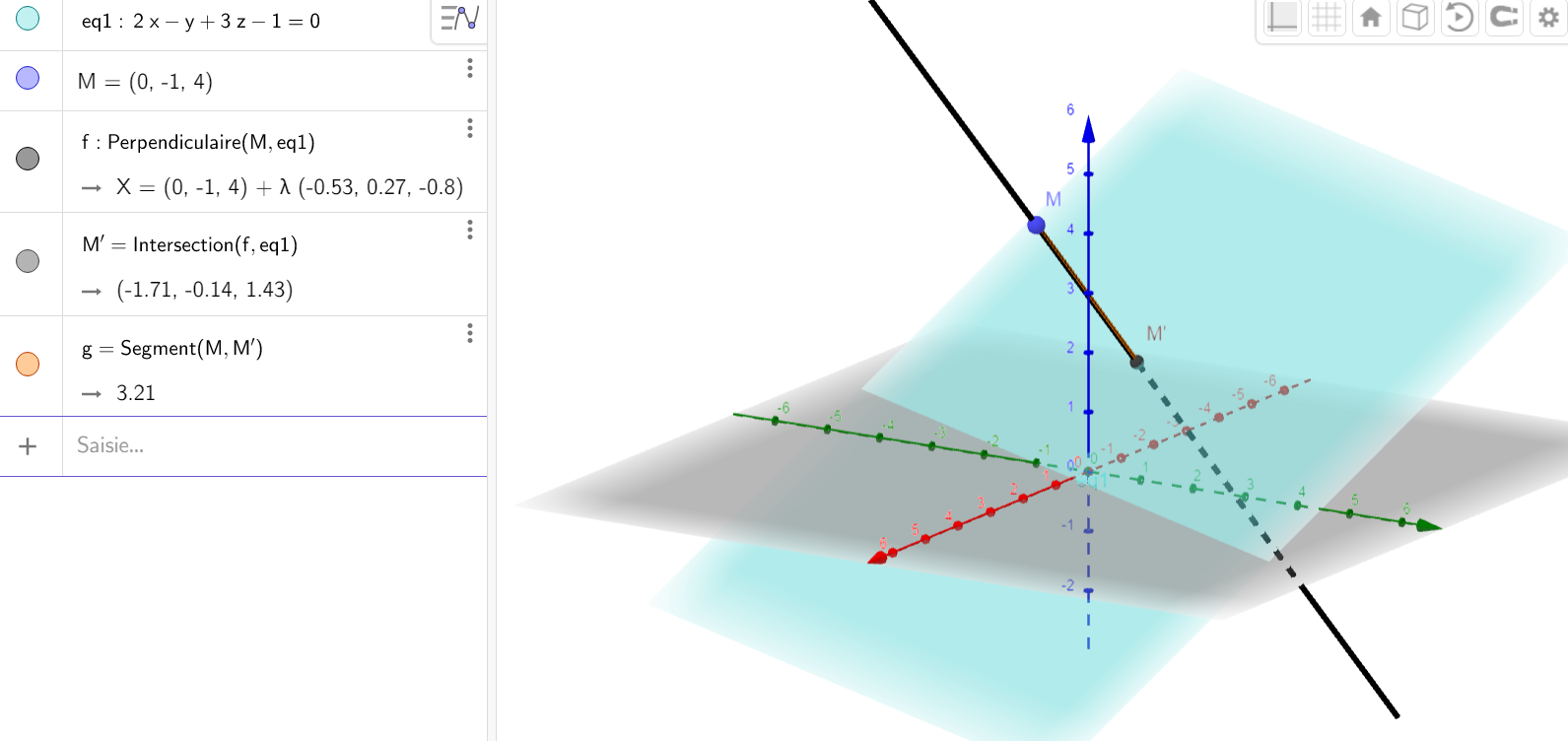
Exemple 1: Dans un repère orthonormal, on considère le point \(M(0;-1; 4)\) et le plan \(\text{P}\) d'équation \(2x - y + 3z - 1 = 0\).
Déterminer les coordonnées du projeté orthonormal \(\text{M'}\) du point \(\text{M}\) sur le point \(\text{P}\).
\(\overrightarrow{n}\begin{pmatrix} 2 \\ - 1 \\ 3 \end{pmatrix}\) est un vecteur normal du plan \(\text{P}\), et donc un vecteur directeur de la droite \((MM')\).
On en déduit une équation paramétrique de la droite \((MM')\) :
\[\left\{ \begin{matrix} x = 2t \\ y = -1-t \\ z = 4 + 3t \end{matrix} \right. \quad , t \in \mathbb{R}\]\(\text{M'}\) est défini comme étant l'intersection de la droite \((MM')\) et du plan \(\text{P}\). On a alors :
\(2 \times 2t - (- 1 - t) + 3 \times (4 + 3t)-1 = 0 \Leftrightarrow 4t + 1 + t + 12 + 9t - 1 = 0 \Leftrightarrow 14t = -12 \Leftrightarrow t = - \dfrac{6}{7}\)
\(\text{M'}\) a donc pour coordonnées \(\left(- \dfrac{12}{7}; - \dfrac{1}{7};\dfrac{10}{7}\right)\)
Ci-dessous : une vue du problème réalisée avec GeoGebra.
B - COORDONNÉES DU PROJETÉ ORTHOGONAL D'UN POINT SUR UNE DROITE
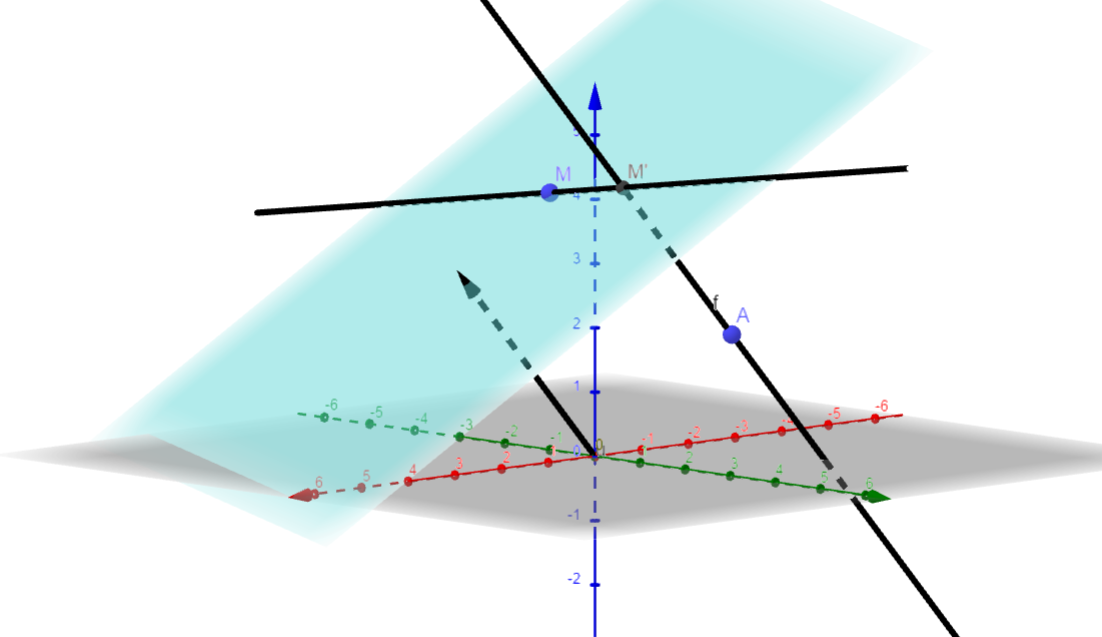
Exemple 2 : Dans un repère orthonormal, on considère le point \(M(0;-1; 4)\) et la droite \(d\) passant par \(\text{A}(-1;2;2)\) et de vecteur directeur \(\overrightarrow{u} \begin{pmatrix} 2 \\ -1 \\ 3 \end{pmatrix}\)
Déterminer les coordonnées du projeté orthonormal \(\text{M'}\) du point \(\text{M}\) sur la droite \(d\).
Une équation paramétrique de la droite droite \(d\) est \(\left\{ \begin{matrix} x =-1+2t \\ y = 2 - t \\ z = 2 + 3t \end{matrix} \right.\), \(t \in \mathbb{R}\)
On cherche le point \(M'(- 1 + 2t;2 - t;2 + 3t)\) de \(d\) tel que \(\overrightarrow{\text{MM'}} \begin{pmatrix} - 1 + 2t \\ 3 - t \\ -2+ 3t \end{pmatrix}\) et \(\overrightarrow{u} \begin{pmatrix} 2 \\ -1 \\ 3 \end{pmatrix}\) soient orthogonaux, c'est à dire :
\(\overrightarrow{\text{MM'}} \cdot \overrightarrow{u}=0 \Leftrightarrow 2 \times (- 1 + 2t) - 1 \times (3 - t) + 3 \times (-2 + 3t) = 0 \Leftrightarrow -2 + 4t - 3 + t - 6 + 9t = 0 \Leftrightarrow {14t} = 11 \Leftrightarrow t = \dfrac{11}{14}\)
\(\text{M'}\) a donc pour coordonnées \(\left(\dfrac{4}{7};\dfrac{17}{14};\dfrac{61}{14}\right)\)
Ci-dessous : deux vues du problème réalisées avec GeoGebra.

C - FORMULE POUR CALCULER LA DISTANCE D'UN POINT À UN PLAN
Soit \(({\text{O};\overrightarrow{i},\overrightarrow{j};\overrightarrow{k}})\) un repère orthonormal de l'espace et \(\text{P}\) le plan d'équation \(ax + by + cz + d = 0\). \(\overrightarrow{n}\begin{pmatrix} a \\ b \\ c \end{pmatrix}\) est un vecteur normal à \(\text{P}\).
On calcule \(\overrightarrow{\text{MM'}} \cdot \overrightarrow{n}\) de deux façons différentes :
Façon 1: (avec les coordonnées)
On a \(\overrightarrow{\text{MM'}} \begin{pmatrix} x_{M'} - x_{\text{M}} \\ y_{M'} - y_{\text{M}} \\ z_{M'} - z_{\text{M}} \end{pmatrix}\) et \(\overrightarrow{n} \begin{pmatrix} a \\ b \\ c \end{pmatrix}\) , d'où :
\(\overrightarrow{\text{MM'}} \cdot \overrightarrow{n}=a(x_{M'} - x_{\text{M}}) + b(y_{M'} - y_{\text{M}}) + c(z_{M'} - z_{\text{M}})=-ax_{\text{M}} - by_{\text{M}} - cz_{\text{M}}+ax_{M'} + by_{M'} + cz_{M'}\)
Or \(M' \in P\), donc \(ax_{M'} + by_{M'} + cz_{M'} + d = 0 \Leftrightarrow ax_{M'} + by_{M'} + cz_{M'} = - d\)
Ainsi \(\overrightarrow{\text{MM'}} \cdot \overrightarrow{n}=-ax_{\text{M}} - by_{\text{M}} - cz_{\text{M}}-d\)
Façon 2: (avec les projetés orthogonaux)
On a (par construction), \(\overrightarrow{\text{MM'}}\) et \(\overrightarrow{n}\) colinéaires car ils sont tous les deux orthogonaux à \(\text{P}\). On a alors :
\(\overrightarrow{\text{MM'}} \cdot \overrightarrow{n}=\left| \left| \overrightarrow{\text{MM'}} \right| \right| \times \left| \left| \overrightarrow{n} \right| \right|\) ou \(\overrightarrow{\text{MM'}} \cdot \overrightarrow{n}=-\left| \left| \overrightarrow{\text{MM'}} \right| \right| \times \left| \left| \overrightarrow{n} \right| \right|\) selon que \(\overrightarrow{\text{MM'}}\) et \(\overrightarrow{n}\) sont de sens opposés ou non.
On obtient donc :
\(\left| {\overrightarrow{\text{MM'}} \cdot \overrightarrow{n}} \right|=\left| \left| \overrightarrow{\text{MM'}} \right| \right| \times \left| \left| \overrightarrow{n} \right| \right|\)
Et \(\left| \left| \overrightarrow{\text{MM'}} \right| \right| = \dfrac{\left| {\overrightarrow{\text{MM'}} \cdot \overrightarrow{n}} \right|}{\left| \left| \overrightarrow{n} \right| \right|}=\dfrac{\left| - ax_{\text{M}} - by_{\text{M}} - cz_{\text{M}} - d \right|}{\sqrt{a^{2} + b^{2} + c^{2} } }=\dfrac{\left| ax_{\text{M}} + by_{\text{M}} + cz_{\text{M}} + d \right|}{\sqrt{a^{2} + b^{2} + c^{2} } }\)
On en déduit donc que la distance du point \(\text{M}\) au plan \(\text{P}\) est \(\dfrac{\left| ax_{\text{M}} + by_{\text{M}} + cz_{\text{M}} + d \right|}{\sqrt{a^{2} + b^{2} + c^{2} } }\)
Revenons à l'exemple 2 :
En appliquant cette formule, on obtient que la distance de \(\text{M}\) au plan \(\text{P}\) est :
\[\dfrac{\left| 2 \times 0 - (- 1) + 3 \times 4 - 1 \right|}{\sqrt{4 + 1 + 9}} = \dfrac{12}{\sqrt{14}} \approx 3.21\]Ce résultat correspond bien au résultat fourni par GeoGebra.
On peut aussi calculer la longueur \(\text{MM'}\), on obtiendra le même résultat.


