LIMITES DE FONCTIONS
1 - LIMITE EN \(+\infty\) ET EN \(-\infty\)
A - LIMITE INFINIE EN \(+\infty\) ET EN \(-\infty\)
Définition
Soit \(f\) une fonction définie sur un intervalle de la forme \(\left\lbrack {a{; +\infty}}\lbrack \right.\) où \(a\) est un réel.
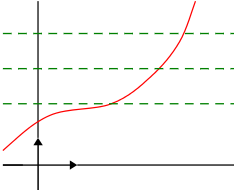
Intuitivement, dire que \(f\) a pour limite \(+\infty\) en \(+\infty\), signifie que lorsque \(x\) prend des valeurs de plus en plus grandes vers \(+\infty\), «les nombres \(f(x)\) correspondants finissent par être aussi grands que l'on veut ».
On note: \({\lim\limits_{x \to{+\infty}}f(x)} = {+\infty}\)
Lorsque \(x\) prend des valeurs de plus en plus grande ,la courbe \(C_{f}\) finit par se situer au dessus de n'importe quelle droite horizontale.
Remarques
De manière plus mathématique (moins intuitive ...) :
Tout intervalle de la forme \(\rbrack{M{; +\infty}}\lbrack\) finit par contenir toutes les valeurs \(f(x)\). On écrit aussi:
Pour tout réel \(M > 0\), il existe un réel \(m\) tel que , si \(x > m\), alors \(f(x) \in \rbrack M; +\infty \lbrack\)
On dit aussi que la fonction \(f\) tend vers \(+\infty\) quand \(x\) tend vers \(+\infty\).
Exemples à connaître :
\(\lim\limits_{x \to +\infty}x = +\infty\),
\(\lim\limits_{x \to +\infty}x^{2} = +\infty\),
\(\lim\limits_{x \to +\infty}x^{3} = +\infty\),
\(\lim\limits_{x \to +\infty}\sqrt{x} = +\infty\)
On définit de la même façon:
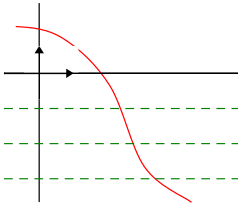
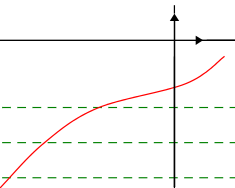
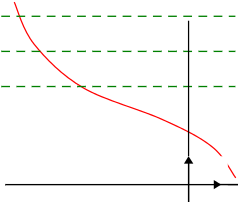
Méthode
Dans la pratique, on peut utiliser la propriété suivante :
B - LIMITE FINIE EN \(+\infty\) ET EN \(-\infty\) ET ASYMPTOTE HORIZONTALE
Définition
Soit \(f\) une fonction définie sur un intervalle de la forme \(\left\lbrack {a{; +\infty}}\lbrack \right.\) où \(a\) est un réel et soit \(L\) un réel donné.
Intuitivement, dire que \(f\) a pour limite \(L\) en \(+\infty\), signifie que lorsque \(x\) prend des valeurs de plus en plus grandes vers \(+\infty\) , «les nombres \(f(x)\) correspondants viennent s'accumuler autour de \(L\)».
On note : \(\lim\limits_{x \to +\infty}f(x) = L\)
On dit que la droite d'équation \(y = L\) est asymptote horizontale à la courbe \(C_{f}\) en \(+\infty\).
Lorsque \(x\) prend des valeurs de plus en plus grandes, la distance \(\text{MN}\) tend vers 0.
La courbe \(C_{f}\) se rapproche sans cesse de la droite d'équation \(y = L\).
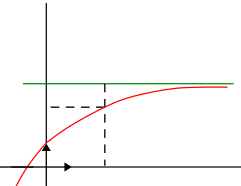
Remarques
De manière plus mathématique (moins intuitive ...) :
Tout intervalle ouvert contenant \(L\) finit par contenir toutes toutes les valeurs \(f(x)\).
On écrit aussi:
Pour tout \(\varepsilon > 0\) (aussi petit qu'il soit) il existe un réel \(m\) tel que , si \(x > m\) , alors \(f(x) \in {\rbrack{L-\varepsilon;{L + \varepsilon}}\lbrack}\) .
On définit de la même façon:
\({\lim\limits_{x \to{-\infty}}f(x)} = L\)
\(f\) est définie sur un intervalle de la forme \(\rbrack\left. -\infty;b \right\rbrack\)
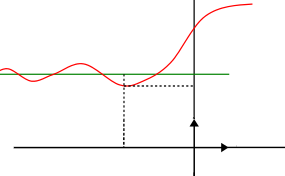
La distance \(\text{MN}\) tend vers \(0\) quand \(x\) tend vers \(-\infty\).
La droite d'équation \(y = L\) est asymptote horizontale à la courbe \(C_{f}\) en \(-\infty\).
Exemples à connaître :
\(\lim\limits_{x \to +\infty}\dfrac{1}{x} = 0\),
\(\lim\limits_{x \to +\infty}\dfrac{1}{x^{2}} = 0\),
\(\lim\limits_{x \to +\infty}\dfrac{1}{x^{3}} = 0\),
\(\lim\limits_{x \to +\infty}\dfrac{1}{\sqrt{x}} = 0\),
\(\lim\limits_{x \to -\infty}\dfrac{1}{x} = 0\),
\(\lim\limits_{x \to -\infty}\dfrac{1}{x^2} = 0\),
\(\lim\limits_{x \to -\infty}\dfrac{1}{x^3} = 0\)
La courbe représentant la fonction \(x \mapsto \dfrac{1}{\sqrt{x}}\) admet l'axe des abscisses comme asymptote en \(+\infty\) ; les trois autres courbes admettent cet axe comme asymptote en \(+\infty\) et en \(-\infty\).
Remarque
Une fonction n'a pas forcément une limite finie ou infinie quand \(x\) tend vers \(+\infty\). ( Par exemple \(x \mapsto \sin x\) , \(x \mapsto \cos x\) ...)
C - ASYMPTOTE OBLIQUE
Définition
Soit \(a\) (\(a \neq 0\)) et \(b\) deux réels et \(C\) la courbe représentant une fonction \(f\) dans un repère.
Dire que la droite d'équation \(y = ax + b\) est asymptote oblique à \(C\) en \(+\infty\) (respectivement en \(-\infty\)) revient à dire que :
(respectivement \(\lim\limits_{x \to -\infty}(f(x)-(ax + b)) = 0\))
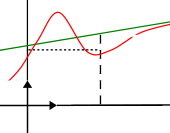
La distance \(\text{MN}\) tend vers \(0\) quand \(x\) tend vers \(+\infty\).
Remarque
Une fonction peut avoir une limite infinie lorsque \(x\) tend vers \(+\infty\) ou vers \(-\infty\) sans que sa courbe possède une asymptote. (c'est le cas de la fonction carrée)
2 - LIMITE EN \(a\) (avec \(a\) réel)
Lorsque que l'on définit la limite d'une fonction \(f\) en un réel \(a\), on considère que \(a \in D_{f}\) ou \(a\) est une borne de \(D_{f}\)
A - LIMITE INFINIE EN \(a\) ET ASYMPTOTE VERTICALE
Définition
Soit \(f\) une fonction.
Intuitivement, dire que \(f\) a pour limite \(+\infty\) en \(a\), signifie que lorsque \(x\) prend des valeurs de plus en plus proches de \(a\), «les nombres \(f(x)\) correspondants finissent par être aussi grands que l'on veut ».
On note : \({\lim\limits_{x \to a}f(x)} = {+\infty}\)
On définit de la même façon \({\lim\limits_{x \to a}f(x)} = {-\infty}\)
On dit que la droite d'équation \(x = a\) est asymptote verticale à la courbe \(C_{f}\).
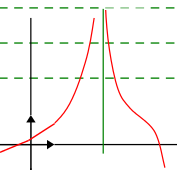
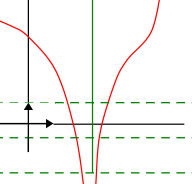
Lorsque \(x\) prend des valeurs de plus en plus proches de \(a\), la courbe \(C_f\) finit par se situer au dessus (et en dessous pour la deuxième figure) de n'importe quelle droite horizontale.
Remarque
Il arrive souvent qu'on soit amené à définir des limites «d'un seul côté de \(a\)».
Naturellement, on introduit les notions de limite à droite en \(a\) et de limite à gauche en \(a\) et on note:
\(\lim\limits_{x \to a^+}f(x)\) et \(\lim\limits_{x \to a^-}f(x)\) ou encore \(\lim\limits_{\substack{x \to a \\ x>a}}f(x)\) et \(\lim\limits_{\substack{x \to a \\ x<a}}f(x)\)
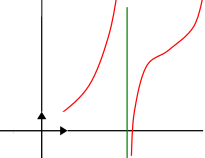
Exemples
\({\lim\limits_{x \to 0^+}\dfrac{1}{x}} = {+\infty}\),
\({\lim\limits_{x \to 0^+}\dfrac{1}{x^{2} } } = {+\infty}\),
\({\lim\limits_{x \to 0^+}\dfrac{1}{x^{3} } } = {+\infty}\),
\({\lim\limits_{x \to 0^+}\dfrac{1}{\sqrt{x} } } = {+\infty}\)
\({\lim\limits_{x \to 0^-}\dfrac{1}{x}} = {-\infty}\),
\({\lim\limits_{x \to 0^-}\dfrac{1}{x^{2} } } = {+\infty}\),
\({\lim\limits_{x \to 0^-}\dfrac{1}{x^{3} } } = {-\infty}\)
Les courbes représentant ces fonctions admettent l'axe des ordonnées comme asymptote verticale.
B - LIMITE FINIE EN \(a\)
On a déjà vu la notion de limite finie en zéro dans le chapitre sur la dérivation en 1ère. La notion de limite finie en \(a\) est identique.
Définition
Soit \(f\) une fonction telle que \(a\) soit dans son ensemble de définition \(D_f\) ou soit une borne de \(D_f\) et soit \(L\) un réel donné.
Intuitivement, dire que \(f\) a pour limite \(L\) en \(a\), signifie que lorsque \(x\) prend des valeurs de plus en plus proches de \(a\) «les nombres \(f(x)\) correspondants viennent s'accumuler autour de \(L\)».
On note: \({\lim\limits_{x \to a}f(x)} = L\)
Remarques
De manière plus mathématique (moins intuitive ...) :
Tout intervalle ouvert contenant \(L\) finit par contenir toutes les valeurs \(f(x)\). On écrit aussi:
Pour tout \(({\varepsilon > 0})\) (aussi petit qu'il soit) les nombres \(f(x)\) finissent par se situer dans l'intervalle \(\rbrack L - \varepsilon;L + \varepsilon \lbrack\).
On admet que si une fonction \(f\) est définie en \(a\) et si \(f\) admet une limite finie en \(a\) , alors \(\lim\limits_{x \to a}f(x) = f(a)\).
C'est le cas, en tout point de l'ensemble de définition, des fonctions polynômes, rationnelles et trigonométriques, de la fonction racine carrée... et des composées de ces fonctions.
Cette remarque nous permet de déterminer rapidement la limite d'une telle fonction en tout point de son ensemble de définition.
Exemples
\({\lim\limits_{x \to 3}\sin{({3{x + 4}})}} = {\sin 13}\),
\({\lim\limits_{x \to 4}\sqrt{x^{2} + 3}} = \sqrt{19}\)
Attention: Comme nous le verrons plus loin, toutes les fonctions n'admettent pas forcément une limite finie en tout point de leur ensemble de définition. (la limite à droite et la limite à gauche peuvent être différentes...)
3 - OPÉRATION SUR LES LIMITES
Ces opérations sont identiques à celles déjà vues avec les suites.
Les théorèmes qui suivent, présentés sous forme de tableaux sont admis.
Pour la plupart d'entre eux, ils sont naturels mais... comme souvent en maths, il y a quelques cas particuliers.
Par convention et pour simplifier :
On note \(\lim f\) et \(\lim g\) les limites de \(f\) et de \(g\), toutes les deux en \(a\) , en \(+\infty\) ou en \(-\infty\).
On note par un point d'interrogation (?) les cas où il n'y a pas de conclusion générale.
On dit qu'il s'agit de cas de formes indéterminées. Ces cas nécessiteront une étude particulière chaque fois qu'ils se présenteront.
Limites de \(kf\) (où \(k\) est un réel donné)
| \(\lim f\) | \(L\) | \(+\infty\) | \(-\infty\) |
|---|---|---|---|
| \(\lim kf\) ( avec \(k > 0\) ) | \(kL\) | \(+\infty\) | \(-\infty\) |
| \(\lim kf\) ( avec \(k < 0\) ) | \(kL\) | \(-\infty\) | \(+\infty\) |
Exemple
Soit la fonction \(g\) définie sur \(\mathbb{R}^*\) par \(g:x \mapsto -\dfrac{2}{x^2}\).
Calculer \(\lim\limits_{x \to 0}g(x)\)
On a \(g = {-2}f\) avec \(f:x \mapsto \dfrac{1}{x^{2}}\)
Comme \(-2<0\) et \({\lim\limits_{x \to 0}f(x)} = {+\infty}\) , on en déduit que \({\lim\limits_{x \to 0}g(x)} = {-\infty}\)
Limites de \(f + g\)
| \(\lim f\) | \(L\) | \(L\) | \(L\) | \(+\infty\) | \(-\infty\) | \(+\infty\) |
|---|---|---|---|---|---|---|
| \(\lim g\) | \(L'\) | \(+\infty\) | \(-\infty\) | \(+\infty\) | \(-\infty\) | \(-\infty\) |
| \(\lim (f+g)\) | \(L+L'\) | \(+\infty\) | \(-\infty\) | \(+\infty\) | \(-\infty\) | ? |
Exemple
Soit la fonction \(h\) définie sur \(\mathbb{R}^{+*}\) par \(h:x \mapsto \sqrt{x} - \dfrac{2}{x^{2}}\).
Calculer \(\lim\limits_{x \to +\infty}h(x)\)
On a \(h = {f + g}\) avec \(f:x \mapsto \sqrt{x}\) et \(g:x \mapsto -\dfrac{2}{x^{2}}\)
Comme \({\lim\limits_{x \to +\infty}f(x)} = {+\infty}\) et \({\lim\limits_{x \to +\infty}g(x)} = 0\) , on en déduit par somme que \({\lim\limits_{x \to +\infty}h(x)} = {+\infty}\).
Limites de \(f \times g\)
| \(\lim f\) | \(L\) | \(L>0\) | \(L>0\) | \(L<0\) | \(L<0\) | \(+\infty\) | \(+\infty\) | \(-\infty\) | \(0\) |
|---|---|---|---|---|---|---|---|---|---|
| \(\lim g\) | \(L'\) | \(+\infty\) | \(-\infty\) | \(+\infty\) | \(-\infty\) | \(+\infty\) | \(-\infty\) | \(-\infty\) | \(+\infty\) ou \(-\infty\) |
| \(\lim (f \times g)\) | \(L \times L'\) | \(+\infty\) | \(-\infty\) | \(-\infty\) | \(+\infty\) | \(+\infty\) | \(-\infty\) | \(+\infty\) | ? |
Exemple
Soit la fonction \(h\) définie sur \(\mathbb{R}^+\) par \(h:x \mapsto (x+2)\sqrt{x}\).
Calculer \(\lim\limits_{x \to 0}h(x)\)
On a \(h = {f \times g}\) avec \(f:x \mapsto x+2\) et \(g:x \mapsto \sqrt{x}\)
Comme \(\lim\limits_{x \to 0}f(x) = 2\) et \(\lim\limits_{x \to 0}\sqrt{x} = 0\), on en déduit par produit que \(\lim\limits_{x \to 0}h(x) = 0\)
Limites de \(\dfrac{f}{g}\)
| \(\lim f\) | \(L\) | \(L\) | \(+\infty\) | \(+\infty\) | \(-\infty\) | \(-\infty\) | \(+\infty\) ou \(-\infty\) | \(L>0\) ou \(+\infty\) | \(L>0\) ou \(+\infty\) | \(L<0\) ou \(-\infty\) | \(L<0\) ou \(-\infty\) | \(0\) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(\lim g\) | \(L'\) | \(+\infty\) ou \(-\infty\) | \(L'>0\) | \(L'<0\) | \(L'>0\) | \(L'<0\) | \(+\infty\) ou \(-\infty\) | \(0^+\) | \(0^-\) | \(0^+\) | \(0^-\) | \(0\) |
| \(\lim \dfrac{f}{g}\) | \(\dfrac{L}{L'}\) | \(0\) | \(+\infty\) | \(-\infty\) | \(-\infty\) | \(+\infty\) | ? | \(+\infty\) | \(-\infty\) | \(-\infty\) | \(+\infty\) | ? |
Remarques
On note \(\lim\limits_{x \to +\infty}g(x) = 0^+\) pour indiquer que \(g(x)\) tend vers \(0\) en restant positive.
On note \(\lim\limits_{x \to +\infty}g(x) = 0^-\) pour indiquer que \(g(x)\) tend vers \(0\) en restant négative.
Exemple
Soit la fonction \(h\) définie sur \(\mathbb{R}^{+*}\) par \(h:x \mapsto \dfrac{2{x - 4}}{\sqrt{x}}\).
Calculer \(\lim\limits_{x \to 0^+}h(x)\)
On a \(h = \dfrac{f}{g}\) ou \(f:x \mapsto 2x-4\) et \(g:x \mapsto \sqrt{x}\)
Comme \({\lim\limits_{x \to 0^+}f(x)} = {- 4}\) et \({\lim\limits_{x \to 0^+}g(x)} = 0^+\) , on en déduit par quotient que \({\lim\limits_{x \to 0^+}h(x)} = {-\infty}\).
4 - LIMITE D'UNE FONCTION COMPOSÉE
Propriété
Soit \(f\), \(g\) et \(h\) trois fonctions telles que \(f(x) = g(h(x))\).
Chacune des lettres \(a\), \(b\) et \(c\) désigne soit un réel, soit \(+\infty\), soit \(-\infty\).
Si \({\lim\limits_{x \to a}h(x)} = b\) et si \({\lim\limits_{x \to b}g(x)} = c\) , alors \(\lim\limits_{x \to a}f(x) = c\)
Dans la pratique, on cherche d'abord la limite \(b\) de \(h\) en \(a\), puis la limite de \(g\) en \(b\).
Preuve intuitive
cas où \(a\), \(b\) et \(c\) sont des réels.
On a \({\lim\limits_{x \to a}h(x)} = b\). Ainsi , lorsque \(x\) tend vers \(a\), les nombres \(h(x)\) se rapprochent de \(b\).
Posons \(h(x) = X\) . On a alors \(f(x) = g(X)\).
Lorsque les nombres \(X\) tendent vers \(b\), alors les nombres \(g(x)\) se rapprochent de \(c\), puisque \(\lim\limits_{x \to b}g(x) = c\).
On en déduit que \({\lim\limits_{x \to a}g(h(x))} = c\)
Exemple
Soit \(f(x) = \sqrt{2{x^{2} - 3}{x + 5}}\).
Calculer \(\lim\limits_{x \to +\infty}f(x)\)
Posons \(X = 2x^2 - 3x + 5\) . On a alors \(f(x) = \sqrt{X}\)
\({\lim\limits_{x \to +\infty}X} = +\infty\) et \(\lim\limits_{x \to +\infty}\sqrt{X} = +\infty\). On en déduit par composition que \({\lim\limits_{x \to +\infty}f(x)} = +\infty\).
Remarque
Le procédé est identique pour une suite définie par \(u_{n} = g(v_n)\). (par exemple la suite définie par \(u_{n} = \sqrt{2n^2-3n+5}\))
5 - THÉORÈMES DE COMPARAISON
A - THÉORÈME DES GENDARMES
Théorème des gendarmes ou théorème d'encadrement : admis
Soit \(f\), \(g\) et \(h\) trois fonctions définies sur un intervalle \(\rbrack{b; +\infty}\lbrack\) où \(b\) est un réel et soit \(L\) un réel donné.
Si pour tout \(x \in \rbrack b; +\infty \lbrack,\ g(x) \leqslant f(x) \leqslant h(x)\) et \(\lim\limits_{x \to +\infty}g(x) = \lim\limits_{x \to +\infty}h(x) = L\), alors \(\lim\limits_{x \to +\infty}f(x) = L\)
Ce théorème reste valable pour des limites en \(-\infty\) et en un réel \(a\).
Il suffit dans les hypothèses de modifier le domaine de validité des inégalités.
Exemple
Soit \(f(x) = \dfrac{\cos x}{x}\).
Calculer \(\lim\limits_{x \to +\infty}f(x)\)
Pour tout \(x \in \mathbb{R}^{+*}\), on a:
\(-1 \leqslant \cos x \leqslant 1\), donc \(-\dfrac{1}{x} \leqslant \dfrac{\cos x}{x} \leqslant \dfrac{1}{x}\).
Or \(\lim\limits_{x \to +\infty}\left(- \dfrac{1}{x}\right) = \lim\limits_{x \to +\infty}\dfrac{1}x = 0\). D'après le théorème des gendarmes, on déduit que\(\lim\limits_{x \to +\infty}f(x) = 0\)
B - COMPARAISON À L'INFINI
Propriété
Soit \(f\) et \(g\) deux fonctions définies sur un intervalle \(\rbrack b ; +\infty \lbrack\) où \(b\) est un réel.
Si pour tout \(x \in \rbrack b; +\infty \lbrack,\ g(x) \leqslant f(x)\) et si \(\lim\limits_{x \to +\infty}g(x) = +\infty\) , alors \(\lim\limits_{x \to +\infty}f(x) = +\infty\).
Si pour tout \(x \in \rbrack b ; +\infty \lbrack,\ f(x) \leqslant g(x)\) et si \(\lim\limits_{x \to +\infty}g(x) = -\infty\) , alors \(\lim\limits_{x \to +\infty}f(x) = -\infty\).
Ce théorème reste valable pour des limites en \(-\infty\).
Preuve
Soit \(M>0\).
\({\lim\limits_{x \to +\infty}g(x)} = {+\infty}\) , il existe donc un réel \(m\) tel que, si \(x > m\), alors \(g(x) \in {\rbrack{M{; +\infty}}\lbrack}\).
Or \(g(x) \leqslant f(x)\) . On en déduit que, si \(x > m\), alors \(f(x) \in {\rbrack{M; +\infty}\lbrack}\).
Ce résultat est vrai pour tout réel \(M > 0\). Donc \(\lim\limits_{x \to +\infty}f(x) = +\infty\)
Le deuxième résultat se démontre de la même façon.
Exemple
Soit \(f(x) = x - \sin x\).
Calculer \(\lim\limits_{x \to +\infty}f(x)\)
Pour tout \(x \in \mathbb{R}\), on a : \({- 1} \leqslant - \sin x\), donc \(x - 1 \leqslant x - \sin x\).
Or \(\lim\limits_{x \to +\infty}(x-1) = +\infty\).
On en déduit que \(\lim\limits_{x \to +\infty}f(x) = +\infty\)
6 - RETOUR SUR LA FONCTION EXPONENTIELLE
A - LIMITES EN L'INFINI
Propriété
\(\lim\limits_{x \to +\infty}e^x = +\infty\) et \(\lim\limits_{x \to -\infty}e^{x} = 0\)
Preuve : exigible
La fonction exponentielle est strictement croissante, on a donc \(e^1 > e^0\) donc \(e > 1\).
On en déduit que la suite \((e^{n})\) est une suite géométrique de raison \(e\) avec \(e > 1\).
Ainsi \(\lim\limits_{n \to +\infty}e^n = +\infty\)
Soit \(M > 0\).
On a \(\lim\limits_{n{\to +\infty}}e^n = +\infty\) , il existe donc \(n_{0}\) tel que si \(n > n_0\), \(e^n \in \rbrack{M; +\infty}\lbrack\)
Or la fonction exponentielle est croissante . Ainsi, si \(x > n > n_{0}\) on a \(e^{x} > e^{n} > M\) et \(e^x \in \rbrack M; +\infty \lbrack\)
Ce résultat est vrai pour tout \(M > 0\).
On en déduit que \(\lim\limits_{x \to +\infty}e^x = +\infty\)
\(\lim\limits_{x \to -\infty}e^x = \lim\limits_{x \to +\infty}e^{- x} = \lim\limits_{x \to +\infty}\dfrac{1}{e^x} = 0\)
B - CROISSANCE COMPARÉE
Propriété
Pour tout entier naturel \(n\), on a: \(\lim\limits_{x \to +\infty}\dfrac{e^{x}}{x^n} =+\infty\)
Preuve : exigible
Pour tout entier naturel \(n\), on considère la fonction \(f_n\), définie sur \(\mathbb{R}^{+*}\) par \(f_n(x) = \dfrac{e^x}{x^{n+1}}\)
\(f_n\) est dérivable sur \(\mathbb{R}^{+*}\) et pour tout \(x \in \mathbb{R}^{+*}\), on a:
\(f'_n(x) = \dfrac{e^{x}{x^{n+1} - (n+1)} e^{x} x^{n}}{x^{2{n + 2} } } = \dfrac{(x-n-1)e^{x}}{x^{n+2}}\)
\(f'_n(x)\) est du signe de \(x-n-1\)

Ainsi, pour tout \(x \in \mathbb{R}^{+*}\), on a:
\(\dfrac{e^{n+1}}{(n+1)^{n+1}} \leqslant \dfrac{e^x}{x^{n+1}}\)
Ce qui donne:
\(\dfrac{xe^{n+1}}{(n+1)^{n+1}} \leqslant \dfrac{e^x}{x^n}\)
Or \(\lim\limits_{x \to +\infty}\dfrac{xe^{n+1}}{(n+1)^{n+1}} = +\infty\), donc en utilisant les théorèmes de comparaison en l'infini, on obtient \(\lim\limits_{x \to +\infty}\dfrac{e^x}{x^n} = +\infty\).
Remarque
En prenant \(n=0\), on retrouve \(\lim\limits_{x \to +\infty}e^x = +\infty\)
En prenant \(n=1\), on obtient une limite importante \(\lim\limits_{x \to +\infty}\dfrac{e^x}x = +\infty\).
C - Limites en \(-\infty\)
Propriété
\(\lim\limits_{x \to -\infty} x e^x = 0\) et pour tout entier naturel \(n\),\(\lim\limits_{x \to -\infty} x^n e^x = 0\)
Preuve
On pose \(X = -x\), ce qui implique que lorsque \(x\) tend vers \(-\infty\), \(X\) tend vers \(+\infty\),
On a alors \(\lim\limits_{x \to -\infty} x e^x =\lim\limits{X \to +\infty} (-X) e^{-X} = -\dfrac{X}{e^X}\).
Or, \(\lim\limits_{X \to +\infty} \dfrac{e^X}X = 0\). Par inverse, cela implique que \(\lim\limits_{X \to +\infty}\dfrac{X}{e^X}=0\),
On en conclut :
On obtient la limite de \(x^n e^x\) en \(-\infty\) de façon identique.
D - Une dernière limite pour la route
Propriété
Preuve
Le taux de variation d'une fonction \(f(x)\) entre \(x = 0\) et un point \(x \neq 0\) est donné par :
Pour la fonction exponentielle \(f(x) = e^x\), cela devient :
Ainsi, \(\dfrac{e^x - 1}{x}\) représente le taux de variation de \(e^x\) en \(0\).
Or la limite du taux de variation lorsque \(x\) tend \(0\) est le nombre dérivé de la fonction \(f\) en \(0\). D'où \(\lim\limits_{x \to 0} \dfrac{e^x - 1}{x} = f'(0)\), où \(f(x) = e^x\).
Par définition la fonction \(x \mapsto e^x\) est dérivable sur \(\mathbb{R}\) et est sa propre dérivée, donc \(f'(0) = e^0 =1\)
D'où \(\lim\limits_{x \to 0}\dfrac{e^x - 1}{x}\).