Feuille d'exercices sur la dérivation
Nombre dérivé d'une fonction en un réel a : quelques rappels
Exercice 1 : Vrai ou faux : restituer les notions du cours
-
Pour savoir si une fonction est dérivable en \(a\), on regarde la limite de \(\dfrac{f(a + h) - f(a)}{h}\) lorsque \(h\) tend vers 0.
-
Pour savoir si une fonction est dérivable en \(a\), on regarde la limite de \(\dfrac{f(x) - f(a)}{x - a}\) lorsque \(x\) tend vers \(a\).
-
Il est possible qu'une fonction ne soit pas dérivable en un réel \(a\).
-
Si une fonction \(f\) est dérivable en \(a\), la tangente à la courbe représentative de \(f\) au point d'abscisse \(a\) admet pour équation \(y = {f'}(a)(x - a) + f(a)\).
Exercice 2 : Déterminer \({f'}{(a)}\) à l'aide d'un graphique
Dans chacun des cas ci-dessous, on considère la courbe représentative \(\text{C}_{f}\) d'une fonction \(f\), et \(\text{A}\) un point de \(\text{C}_{f}\) d'abscisse \(a\). Déterminer \({f'}{(a)}\).
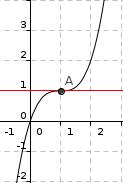 2.
2. 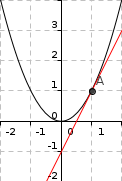 3.
3. 
Exercice 3 : Calculer le nombre dérivé
Déterminer si le nombre dérivé de la fonction \(f\) en \(a\) existe et, si c'est le cas, calculer \({f'}{(a)}\).
-
\(f:x \mapsto x\sqrt{x}\) , \(a = 0\).
-
\(f:x \mapsto \left| {x - 3} \right|\) , \(a = 3\).
-
\(f:x \mapsto x^{2} + x + 1\) , \(a = {- 1}\)
-
\(f:x \mapsto x^{2}\sqrt{x}\) , \(a = 0\)
-
\(f:x \mapsto \left| {x - 5} \right|\) , \(a = 3\)
Formules de dérivation : quelques rappels
Exercice 4
\(D\) représente un intervalle ou une réunion d'intervalles disjoints.
Soit \(u\) et \(v\) deux fonctions dérivables sur \(D\) et \(k\) un réel.
Déterminer la fonction dérivée et l'ensemble de dérivabilité:
- \(f:x \mapsto k\) \((k \in \mathbb{R})\)
- \(f:x \mapsto x\)
- \(f:x \mapsto \sqrt{x}\)
- \(f:x \mapsto x^{n}\) \((n \in \mathbb{Z}^*)\)
- \(ku\)
- \(u + v\)
- \(uv\)
- \(\dfrac{1}{v}\)
- \(\dfrac{u}{v}\)
Compléter :
Toute fonction polynôme est dérivable sur ...
Toute fonction rationnelle est dérivable ...
La notation \(f \circ g\) ou \(v \circ u\)
Pour les exercices concernant les composées de fonctions, il faut toujours en premier lieu déterminer l'ensemble de définition de \(f \circ g\) avant de donner une expression de \(f \circ g{(x)}\)
Exercice 5 : Déterminer \(f \circ g\) et \(g \circ f\)
On considère les fonctions : \(f:x \mapsto \dfrac{1}{x - 3}\) et \(g:x \mapsto x + 4\)
-
Déterminer \(f \circ g\) .
-
Déterminer \(g \circ f\) .
Exercice 6 : La notation \(f^{2}\)
Dans chacun des cas ci-dessous définir \(f^{2}\)
-
\(f:x \mapsto x\)
-
\(f:x \mapsto \dfrac{1}{x}\)
-
\(f:x \mapsto {4x} - 3\)
Attention : Ne pas confondre cette notation avec la puissance d'une fonction pour la multiplication des fonctions.
Par exemple, \(\sin^{2}\) désigne couramment le carré de la fonction sinus.
Généralement, le contexte de l'exercice, nous évite de faire cette confusion malheureuse.
Exercice 7 : Trouver u et v
Dans chacun des cas, déterminer une expression et des fonctions \(v\) et \(u\) telles que \(f\)=\(v \circ u\).
Dans cet exercice, on ne tient pas compte des ensembles de définition.
-
\(f:x \mapsto \dfrac{4}{x - 3} + 5\)
-
\(f:x \mapsto (2x - 5)^{2} - 3\)
-
\(f:x \mapsto - \dfrac{1}(3 - x)^{2}\)
-
\(f:x \mapsto \sqrt{3x - 5}\)
-
\(f:x \mapsto 3\sqrt{x} - 5\)
-
\(f:x \mapsto \text{e}^{2x - 5}\)
-
\(f:x \mapsto 2{\text{e}^{x} - 5}\)
-
\(f:x \mapsto \text{e}^{- x}\)
Exercice 8 : Dérivées de fonctions composées
Sans se préoccuper des ensembles de définition et de dérivabilité, déterminer dans chacun des cas de l'exercice 7 les dérivées des fonctions \(u\), \(v\) puis \(f\).
-
\(f:x \mapsto \dfrac{4}{x - 3} + 5\) : \(v(x) = 4x + 5\) et \(u(x) = \dfrac{1}{x - 3}\)
-
\(f:x \mapsto (2x - 5)^{2} - 3\) : \(v(x) = {x^{2} - 3}\) et \(u(x) = 2x - 5\)
-
\(f:x \mapsto - \dfrac{1}{(3 - x)^2}\) : \(v(x) = - \dfrac{1}{x^2}\) et \(u(x) = {3 - x}\)
-
\(f:x \mapsto \sqrt{3x} - 5\) : \(v(x) = \sqrt{x}\) et \(u(x) = 3x- 5\)
-
\(f:x \mapsto 3\sqrt{x} - 5\) : \(v(x) = 3x - 5\) et \(u(x) = \sqrt{x}\)
-
\(f:x \mapsto \text{e}^{2x - 5}\) : \(v(x) = \text{e}^{x}\) et \(u(x) = 2x - 5\)
-
\(f:x \mapsto 2{\text{e}^{x} - 5}\) : \(v(x) = 2x - 5\) et \(u(x) = \text{e}^x\)
-
\(f:x \mapsto \text{e}^{- x}\) : \(v(x) = \text{e}^{x}\) et \(u(x) = {- x}\)
Dérivées successives
Exercice 9 : Dérivées successives
-
Dans chacun des cas ci-dessous, démontrer que la fonction proposée est dérivable sur I, et calculer sa dérivée . Étudier alors si la fonction dérivée admet une dérivée seconde sur I, et si c'est le cas, calculer cette dérivée seconde.
a. \(f:x \mapsto x^{4} - 3x^3 + 2\) sur \(\mathbb{R}\)
b. \(g:x \mapsto \dfrac{1}{x}\) sur \(\rbrack{0; + \infty}\lbrack\)
c. \(h(x) = \sqrt{x}\) sur \(\left\lbrack {1;3} \right\rbrack\)
d. \(i:x \mapsto (- 2x + 1)^3\) sur \(\mathbb{R}\)
-
Lorsque c'est possible, on peut continuer la dérivation . On obtient alors les dérivées successives de la fonction \(f\) : dérivée troisième \(f^{(3)}\), dérivée quatrième \(f^{(4)}\) ...
Calculer, lorsque c'est possible, les dérivées troisième et quatrième des fonctions vues précédemment.
Convexité, concavité, points d'inflexion
Exercice 10 : À partir d'une courbe
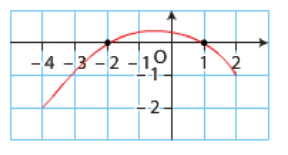
Pour chaque courbe, déterminer les intervalles sur lesquels la fonction \(f\) est convexe ou concave. Préciser les éventuels points d'inflexion. On considère que le comportement de la courbe se poursuit de manière identique en dehors de la fenêtre.
 2.
2. 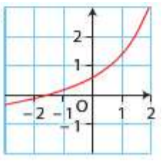 3.
3. 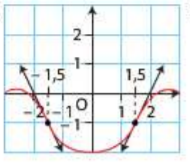 4.
4. 
Exercice 11 : À partir d'une courbe
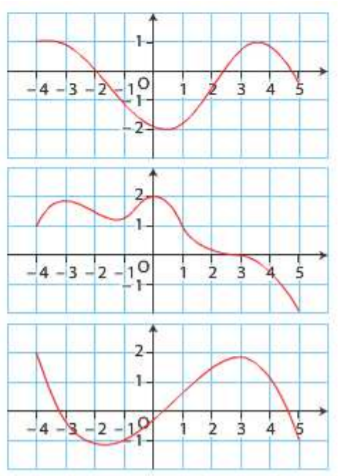
Parmi les trois courbes ci-dessus, déterminer celle qui représente une fonction \(f\) vérifiant :
-
\(f\) est concave sur \([-4 ; -2]\) et sur \([4 ; 5]\)
-
\(f'\) s'annule au moins trois fois
-
la représentation graphique de \(f\) admet quatre points d'inflexion.
Exercice 12 : À partir d'un tableau de variation de \(f'\)
Voici le tableau de variation de la fonction \(f'\) d'une fonction dérivable sur \(\mathbb{R}\).

-
Déterminer le sens de variation de \(f\)
-
Déterminer la convexité de \(f\)
-
Tracer dans un repère une courbe pouvant représenter \(f\).
Exercice 13 : À partir du tableau de signe de \(f''\)
Voici le tableau de signe de la fonction \(f''\) d'une fonction deux fois dérivable sur \(\mathbb{R}\).

-
Déterminer le sens de variation de \(f'\)
-
Déterminer la convexité de \(f\) ainsi que les abscisses des éventuels points d'inflexions.
-
Tracer dans un repère une courbe pouvant représenter \(f\).
Exercice 14 : Position par rapport aux tangentes et inégalités
Dans le repère ci-dessous, on a représenté la courbe de la fonction \(f\) définie sur \(\mathbb{R}\) par \(f(x) = \dfrac{1}{2}x^{2} + {\dfrac{3}{4}x} - 1\) ainsi que sa tangente au point d'abscisse 2.
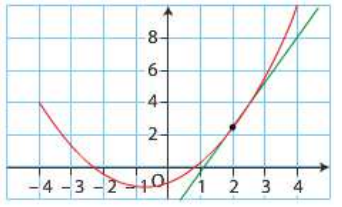
-
Déterminer graphiquement la convexité de \(f\) sur l'intervalle \([-4; 4]\).
-
Pourquoi peut-on étendre ce résultat à \(\mathbb{R}\) ?
-
En déduire que, pour tout \(x \in \mathbb{R}\) , on a \(\dfrac{1}{2}x^{2} + {\dfrac{3}{4}x} - 1 \geqslant \dfrac{11}{4}x - 3\)
-
Montrer alors que \(x^{2} \geqslant 4x - 4\)
Exercice 15 : Position par rapport aux tangentes et inégalités
\(f\) est la fonction définie sur \(\left\lbrack {0; + \infty}\lbrack \right.\) par \(f(x) = \sqrt{x}\).
On note \(\text{C}_{f}\) sa courbe représentative dans un repère.
-
Rappeler la convexité de \(f\).
-
Déterminer une équation de la tangente à \(\text{C}_{f}\) au point d'abscisse 1.
-
En déduire que, pour tout \(x\) de \(\left\lbrack {0; + \infty}\lbrack \right.\), \(\sqrt{x} \leqslant \dfrac{1}{2}x + \dfrac{1}{2}\)
Exercice 16 : Convexité à partir de la courbe représentative de f'
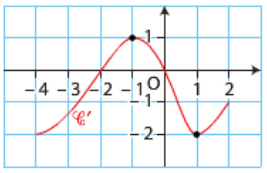
Dan un repère, on a tracé la courbe \(\text{C}_{f'}\) de la fonction dérivée d'une fonction \(f'\) dérivable sur un intervalle \([-4 ; 2]\).
Déterminer, par lecture graphique, la convexité de \(f\).
Exercice 17
Dans chacun des cas, déterminer la convexité de la fonction et préciser les abscisses des éventuels points d'inflexion.
-
\(f\) est une fonction deux fois dérivable sur \([-4 ; 2]\) dont la dérivée \(f''\) est représentée ci-dessous
-
\(g\) est une fonction deux fois dérivable sur \([-3 ; 1]\) dont la dérivée \(g''\) est représentée ci-dessous.

Exercice 18 : Lien entre les représentations graphiques de \(f\) et \(f''\)
Dans un repère, on a tracé la courbe représentative d'une fonction \(f\) deux fois dérivable sur \([-1 ; 3]\).
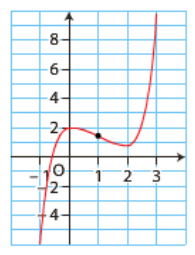
Parmi les trois courbes ci-dessous, laquelle représente celle de la fonction dérivée seconde \(f''\) de \(f\) ?
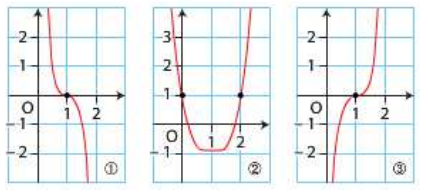
Étude du signe de \(f''\) pour déterminer la concavité
Exercice 19
\(f\) est la fonction définie sur \(\mathbb{R}\) par \(f(x) = 2x^{3} - 3x^{2} - 12x + 4\)
-
Déterminer le signe de \(f''(x)\) suivant les valeurs de \(x\).
-
En déduire la convexité de \(f\).
-
Vérifier le résultat à l'aide d'une calculatrice.
Exercice 20
\(f\) est la fonction définie sur \(\mathbb{R}\) par \(f(x) = {x^{4} + {2x^3} + {12x^2} - {8x} - 6}\)
-
Déterminer le signe de \(f''(x)\) suivant les valeurs de \(x\).
-
En déduire la convexité de \(f\).
-
Vérifier le résultat à l'aide d'une calculatrice.
Exercice 21
\(f\) est la fonction définie sur \(\mathbb{R}\) par \(f(x) = {x^{4} - {10x}^{3} + {36x}^{2} + 1}\)
-
Déterminer le signe de \(f''(x)\) suivant les valeurs de \(x\).
-
En déduire la convexité de \(f\).
-
Vérifier le résultat à l'aide d'une calculatrice.
Exercice 22
\(f\) est la fonction définie sur \(\mathbb{R}\) par \(f(x) = {\text{e}^{x} - \dfrac{x^2}{2} + 7}\)
-
Déterminer le signe de \(f''(x)\) suivant les valeurs de \(x\).
-
En déduire la convexité de \(f\).
-
Vérifier le résultat à l'aide d'une calculatrice.
Exercice 23 : Position par rapport aux tangentes
Soit \(f\) la fonction définie sur \(\mathbb{R} - \left\{ 1 \right\}\) par :
On note \(\text{C}_{f}\) sa courbe dans un repère.
Étudier la position des tangentes à \(\text{C}_{f}\) en 4 et en -4 par rapport à la courbe \(\text{C}_{f}\) .
Exercice 24 : Famille de fonctions
Pour tout entier \(n\), on considère la fonction \(f_{n}\) définie sur \(\mathbb{R}\) par :
On note \(\text{C}_{n}\) la courbe représentative de \(f_{n}\).
Montrer que \(\text{C}_{n}\) admet un point d'inflexion pour tout entier \(n\).
Exercice 25 : Position par rapport aux tangentes
Soit \(f\) la fonction définie sur \(\mathbb{R}\) par \(f(x) = ax^{5} + bx^4 + cx^3 + dx\) où \(a\), \(b\), \(c\) et \(d\) sont des réels avec \(a \neq 0\).
Déterminer à quelle condition la courbe représentative \(\text{C}_{f}\) de \(f\) dans un repère admet exactement deux points d'inflexion.
Exercice 26 : Position par rapport aux sécantes et moyenne
-
En utilisant les représentations graphiques ci-dessous, compléter les propriétés suivantes que nous allons seulement conjecturer.
-
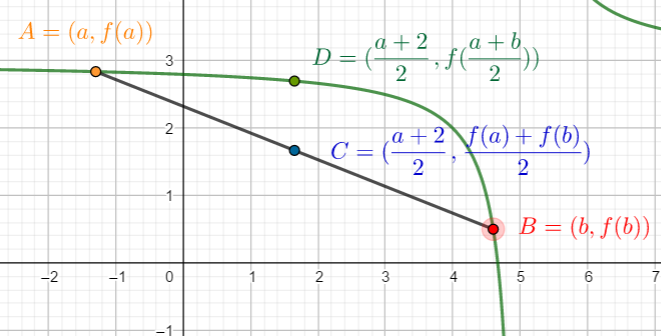
Si \(f\) est une fonction convexe sur un intervalle \(\text{I}\), alors \(f{(\dfrac{a + b}{2})} \leqslant {}\)
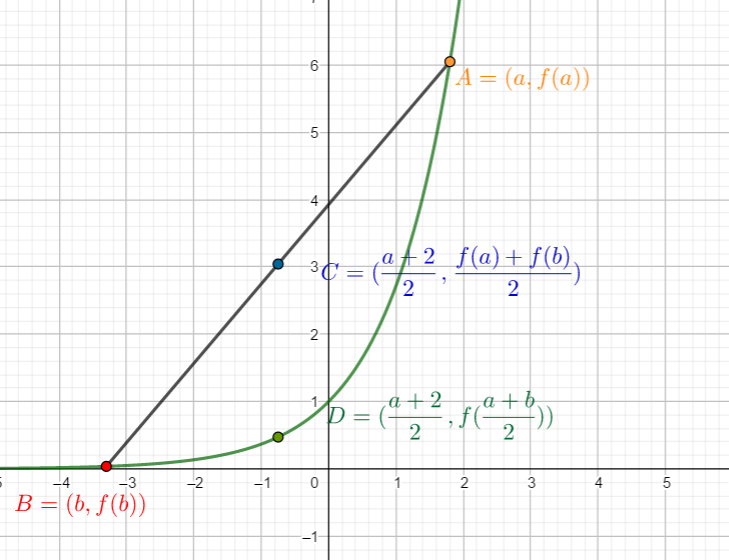
-
Si \(f\) est une fonction concave sur un intervalle I, alors \(f{(\dfrac{a + b}{2})} \geqslant {}\)
-
-
Soit \(a\) et \(b\) deux réels strictement positifs, tels que \(a < b\).
Dans chaque cas, démontrer l'inégalité en étudiant la convexité d'une fonction bien choisie.
a. \(\dfrac{\text{e}^{a + b}}{2} \leqslant \dfrac{\text{e}^{a} + \text{e}^b}{2}\)
b. \(\sqrt{\dfrac{a + b}2} \geqslant \dfrac{\sqrt{a} + \sqrt{b}}2\)
c. \(\dfrac{2}{a + b} \leqslant \dfrac{1}{2a} + \dfrac{1}{2b}\)
d. \(\dfrac{a^2 + 2ab + b^2}{4} \leqslant \dfrac{a^{2} + b^2}{2}\)
Exercice 27 : Vu au bac 2023
Soit la fonction \(f :x \mapsto \dfrac{x-3}{1-x^2}\). On note \(C_f\) sa courbe représentative.
-
Prouver que pour tout \(x \in \rbrack -1;1 \lbrack\), \(f''(x)=\dfrac{2\lbrack x^3-9x^2+3x-3 \rbrack}{(1-x^2)^3}\)
-
À l'aide des études des signes de \(x^3-9x^2\) et \(3x-3\), déduire la convexité de \(f\) sur l'intervalle \(\rbrack -1;1 \lbrack\).
-
Déterminer une équation de la tangente \(T\) à \(C_f\) au point d'abscisse \(0\).
-
On considère la fonction mystere qui prend une liste de nombres L en paramètre:
def mystere(L): M=L[0] for i in range(len(L)): if L[i]>M: M=L[i] return MQue permet de déterminer cette fonction mystere ?
-
On souhaite créer une liste de valeurs comprises entre \(-0.9\) et \(0.9\) avec un pas de \(0.1\).
Compléter le programme Python suivant:
def intervalle(): L=[] D=-0.9 while D<1: ... ... return L -
À l'aide des questions précédentes, écrire un programme la plus grande valeur de \(\Delta\) telle que \(x\) est dans la liste
[-0.9,-0.8,-0.7,...,0.7,0.8,0.9].
