Feuille d'exercices sur les droites et plans de l'espace

Positions relatives

Exercice 1: Vrai ou faux

Dans l'espace :

Trois droites concourantes (qui se coupent en un même point) sont coplanaires.
Deux droites parallèles à un même plan sont parallèles entre elles.
Deux plans parallèles à un même troisième sont parallèles entre eux.
Une droite et un plan parallèles à une même droite sont parallèles entre eux.
Une droite et un plan parallèles à un même plan sont parallèles entre eux.

Pour les exercices 2, 3 et 4, on considère le cube ci-dessous:

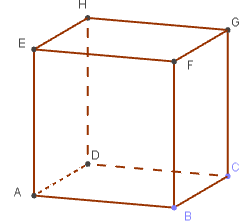
Exercice 2: Entre deux droites

Dans chacun des cas, donner la position des droites :

$\text{(AB)}$ et $\text{(CG)}$
$\text{(AF)}$ et $\text{(GH)}$
$\text{(AC)}$ et $\text{(FH)}$
$\text{(CE)}$ et $\text{(DF)}$
$\text{(BH)}$ et $\text{(AE)}$

Exercice 3 : Entre une droite et un plan

Dans chacun des cas, donner la position de la droite et du plan :

$\text{(AB)}$ et $\text{(CDH)}$
$\text{(AC)}$ et $\text{(BDF)}$
$\text{(BG)}$ et $\text{(CDE)}$
$\text{(AG)}$ et $\text{(CFH)}$
$\text{(BC)}$ et $\text{(FAD)}$
$\text{(AB)}$ et $\text{(ACD)}$

Exercice 4: Entre deux plans

Dans chacun des cas, donner la position des plans :

$\text{(ABC)}$ et $\text{(EGH)}$
$\text{(ABG)}$ et $\text{(CDE)}$
$\text{(CAF)}$ et $\text{(DGH)}$
$\text{(FHC)}$ et $\text{(BDE)}$
$\text{(FAH)}$ et $\text{(BCG)}$

Exercice 5: Dans un tétraèdre

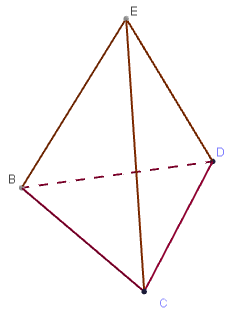
Dans chacun des cas, étudier les positions des droites et plans.

$\text{(EB)}$ et $\text{(CD)}$
$\text{(EC)}$ et $\text{(BCD)}$
$\text{(EBC)}$ et $\text{(ECD)}$
$\text{(EC)}$ et $\text{(BD)}$

Correction des exercices 3 - 4 - 5

Exercice 6 : Dans une pyramide - intersections

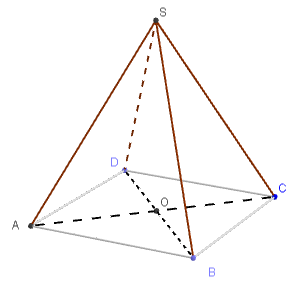
Soit $\text{SABCD}$ une pyramide à base carrée. $\text{O}$ est le centre du carré $\text{ABCD}$.

Déterminer l'intersection de $\text{(SAB)}$ et $\text{(SBC)}$.
Déterminer l'intersection de $\text{(SAC)}$ et $\text{(SBD)}$.
Étudier la position de $\text{(SB)}$ et $\text{(AC)}$.
Déterminer l'intersection de $\text{(SAB)}$ et $\text{(SCD)}$.

On pourra utiliser le théorème du toit:

Si $\text{P}$ et $\text{P'}$ deux plans sécants contiennent deux droites parallèles $\Delta$ et $\Delta'$, alors l'intersection de $\text{P}$ et $\text{P'}$ est une droite parallèle à $\Delta$ et $\Delta'$.

Exercice 7

Dans le cube ci-dessous, $\text{M}$, $\text{N}$ et $\text{P}$ sont les milieux respectifs de $\text{[CD]}$, $\text{[EH]}$ et $\text{[BF]}$.

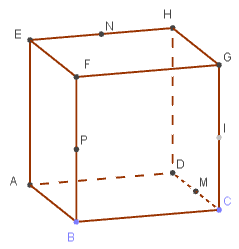
Dans chacun des cas, étudier les positions relatives de :

$\text{(MN)}$ et $\text{(GH)}$
$\text{(MP)}$ et $\text{(DF)}$
$\text{(NP)}$ et $\text{(CDG)}$
$\text{(EM)}$ et $\text{(BFG)}$
$\text{(AMN)}$ et $\text{(BCG)}$
$\text{(MPG)}$ et $\text{(ADE)}$

Exercice 8: Droites coplanaires

Dans le cube de l' Exercice 7 on note $\text{I}$ le milieu de $\text{[CG]}$.

Dire si les droites sont coplanaires ou non ?

$\text{(BC)}$ et $\text{(EH)}$
$\text{(AG)}$ et $\text{(BH)}$
$\text{(AG)}$ et $\text{(EI)}$
$\text{(BH)}$ et $\text{(EI)}$

Exercice 9: Utilisation des symboles mathématiques

On considère le cube de l' Exercice 7 .

Compléter, en utilisant les symboles ${} \in {}$, ${} \notin {}$, ${} \subset {}$ et ${} \not\subset {}$.

$\text{N}$ ... $\text{(EH)}$
$\text{A}$ ... $\text{(EPM)}$
$\text{(BM)}$ ... $\text{(ABC)}$
$\text{(PD)}$ ... $\text{(EFD)}$
$\text{B}$ ... $\text{(EGP)}$
$\text{M}$ ... $\text{(NDC)}$
$\text{(MN)}$ ... $\text{(EHD)}$
$\text{F}$... $\text{(ENG)}$

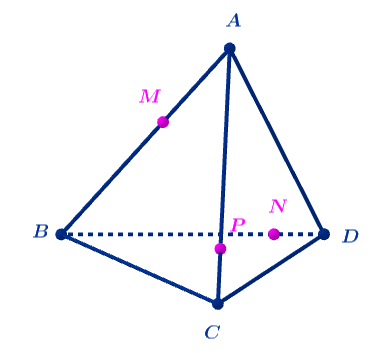
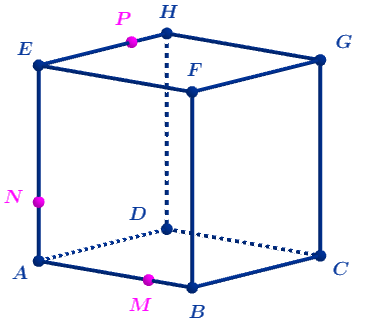
Exercice 10: Sections de solides

Dans chacun des cas, déterminer la section du solide par le plan $\text{(MNP)}$.

C'est à dire (quand elles existent) les intersections avec chacune des faces du solide donné.

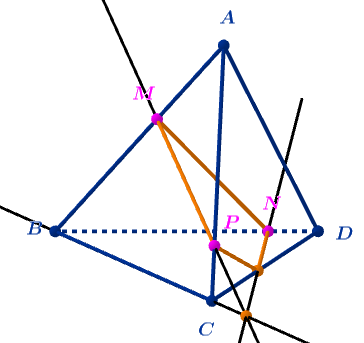
Correction

Cube

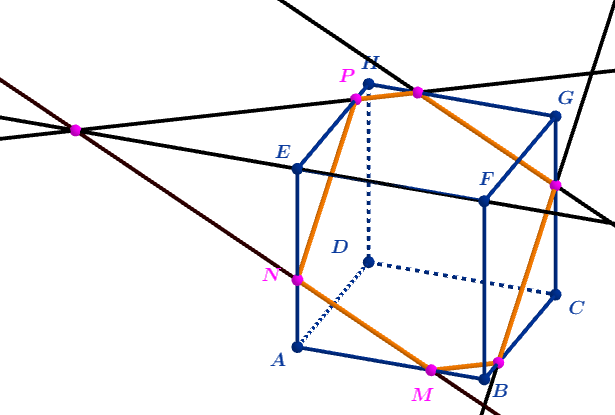
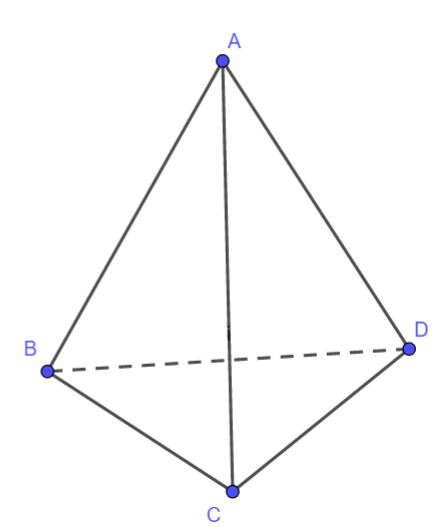
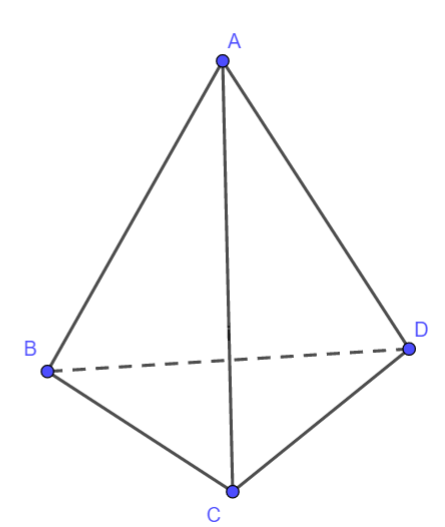
Exercice 11: Intersections et points alignés

Soit un tétraèdre $\text{ABCD}$, de sommet $\text{A}$. Les points $\text{I}$ et $\text{J}$ appartiennent respectivement aux arêtes $\text{[AB]}$ et $\text{[AC]}$ de telle sorte que $\text{(IJ)}$ et $\text{(BC)}$ ne soient pas parallèles.

Déterminer l'intersection de $\text{(IJ)}$ et de $\text{(BCD)}$.
En déduire l'intersection des plans $\text{(DIJ)}$ et $\text{(BCD)}$.
Que devient cette intersection si $\text{(IJ)}//\text{(BC)}$ ?
Soit maintenant un point $\text{K}$ sur $\text{[AD]}$ , de telle sorte que $\text{(IK)}$ et $\text{(BD)}$ ne soient pas parallèles.

On note $\text{M}$, $\text{N}$ et $\text{P}$ les intersections respectives de $\text{(IJ)}$ et $\text{(BC)}$, de $\text{(IK)}$ et $\text{(BD)}$ et de $\text{(JK)}$ et $\text{(CD)}$.

Démontrer que les points $\text{M}$, $\text{N}$ et $\text{P}$ sont alignés.

Exercice 12: Droites parallèles

Dans un cube $\text{ABCDEFGH}$, le point $\text{M}$ appartient à l'arête $\text{[AB]}$ et le point $\text{N}$ est l'intersection de la droite $\text{(AD)}$ avec le plan $\text{(FHM)}$.

Démontrer que $\text{(FH)}//\text{(MN)}$.

Exercice 13

Soit le parallélépipède suivant constitué de deux cubes superposés.

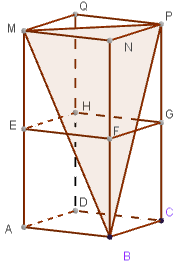
Déterminer l'intersection du plan $\text{(MPB)}$ avec la droite $\text{(NG)}$.
Déterminer l'intersection du plan $\text{(MPB)}$ avec la droite $\text{(EN)}$.
En déduire l'intersection du plan $\text{(MPB)}$ avec le plan $\text{(ENG)}$
Démontrer que l'intersection obtenue à la question 3 est parallèle à la droite $\text{(EG)}$.

Exercice 14

Soit la pyramide SABCD dont la base est un parallélogramme.

$\text{M}$ et $\text{N}$ appartiennent au plan $\text{(SAB)}$ et $\text{P}$ appartient au plan $\text{(SBC)}$.

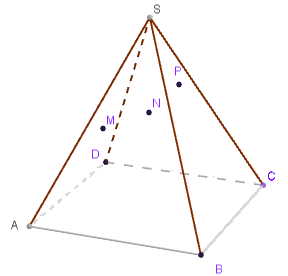
Déterminer l'intersection des plans $\text{(SAB)}$ et $\text{(SCD)}$ et l'intersection des plans $\text{(MNP)}$ et $\text{(SAB)}$.
En déduire l'intersection des plans $\text{(MNP)}$ et $\text{(SCD)}$.
Construire la section de la pyramide par le plan $\text{(MNP)}$.

Vecteurs de l'espace

Dans les exercices 15 à 17, on considère la figure suivante. Sur chaque arête, on a indiqué le milieu de celle-ci.

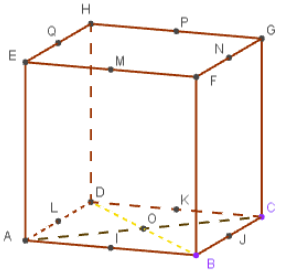
Exercice 15 : vecteur égaux - translations

Dans chaque cas, donner deux vecteurs égaux au vecteur donné :

a. $\overrightarrow{\text{BF}}$

b. $\overrightarrow{\text{BC}}$

c. $\overrightarrow{\text{BM}}$

d. $\overrightarrow{\text{IL}}$

e. $\overrightarrow{\text{OL}}$
Dans chaque cas, déterminer:

a. l'image de $\text{d}$ par la translation de vecteur $\overrightarrow{\text{AF}}$.

b. l'image de $\text{I}$ par la translation de vecteur $\overrightarrow{\text{LP}}$.

c. l'image de $\text{d}$ par la translation de vecteur $\overrightarrow{\text{PN}}$.

Exercice 16 : Trouver le point manquant - combinaisons linéaires

Compléter les égalités suivantes en utilisant les points de la figure :

$\overrightarrow{\text{A...}} = \dfrac{1}{2} \overrightarrow{\text{AD}}$	$\overrightarrow{\text{B...}} = \overrightarrow{\text{BC}} + \overrightarrow{\text{BF}}$	$\overrightarrow{\text{B...}} = \dfrac{1}{2} \overrightarrow{\text{BC}} + \overrightarrow{\text{CG}}$
$\overrightarrow{\text{I...}} = - \overrightarrow{\text{IA}}$	$\overrightarrow{\text{...H}} = \overrightarrow{\text{BD}} + \overrightarrow{\text{BF}}$	$\overrightarrow{\text{A...}} = \dfrac{1}{2} \overrightarrow{\text{AD}} + \overrightarrow{\text{BF}} - \overrightarrow{\text{BA}}$
$\overrightarrow{\text{B...}} = 2 \overrightarrow{\text{EQ}}$	$\overrightarrow{\text{B...}} = \overrightarrow{\text{BA}} + \overrightarrow{\text{DH}}$	$\overrightarrow{\text{B...}} = \dfrac{1}{2}\overrightarrow{\text{BA}} + \overrightarrow{\text{BC}} + \overrightarrow{\text{BF}}$
$\overrightarrow{\text{H...}} = -2 \overrightarrow{\text{BI}}$	$\overrightarrow{\text{B...}} = \overrightarrow{\text{CK}} + \overrightarrow{\text{DH}}$	$\overrightarrow{\text{L...}} = \overrightarrow{\text{HG}} - \dfrac{1}{2} \overrightarrow{\text{AD}} + \overrightarrow{\text{CP}}$

Exercice 17 : Décomposer un vecteur dans une base

Décomposer les vecteurs $\overrightarrow{\text{AC}}$, $\overrightarrow{\text{BP}}$, $\overrightarrow{\text{AG}}$ et $\overrightarrow{\text{MC}}$ dans la base $({\overrightarrow{\text{DA}},\overrightarrow{\text{DH}},\overrightarrow{\text{DC}}})$

Exercice 18 : Relation de Chasles

Soit $\text{A}$, $\text{B}$, $\text{C}$ et $\text{D}$ quatre points non coplanaires de l'espace.

Montrer que ${\overrightarrow{\text{AC}} + \overrightarrow{\text{DB}}} = {\overrightarrow{\text{AB}} + \overrightarrow{\text{DC}}}$

Exercice 19 : Représenter des combinaisons linéaires

Sur la figure ci-dessous, représenter les points :

a. $\text{I}$ défini par $\overrightarrow{\text{AI}} = \overrightarrow{\text{BF}} + \dfrac{1}{2} \overrightarrow{\text{BC}}$

b. $\text{J}$ défini par $\overrightarrow{\text{AJ}} = \overrightarrow{\text{AB}} + \overrightarrow{\text{AD}} + \dfrac{1}{2} \overrightarrow{\text{AE}}$

c. $\text{K}$ image de $\text{I}$ par la translation de vecteur $\overrightarrow{\text{EB}}$

d. $\text{L}$ défini par $\overrightarrow{\text{DL}} = \dfrac{1}{2} \overrightarrow{\text{DA}} + \dfrac{1}{2} \overrightarrow{\text{DC}} + \dfrac{1}{2} \overrightarrow{\text{DH}}$

e. $\text{M}$ image de $\text{C}$ par la translation de vecteur $\dfrac{3}{4}\overrightarrow{\text{AE}}$

Points alignés, parallélisme

Exercice 20 : Alignement

Soit $\text{A}$, $\text{B}$ et $\text{C}$ trois points non alignés et les points $\text{D}$ et $\text{E}$ définis par :

$\overrightarrow{\text{AD}} = \dfrac{1}{2} \overrightarrow{\text{AB}}$ et $\overrightarrow{\text{BE}} = 3 \overrightarrow{\text{AC}} - 2\overrightarrow{\text{AB}}$

En exprimant les vecteurs $\overrightarrow{\text{CD}}$ et $\overrightarrow{\text{CE}}$ comme une combinaison linéaire des vecteurs $\overrightarrow{\text{AB}}$ et $\overrightarrow{\text{AC}}$, montrer que $\text{C}$, $\text{D}$ et $\text{E}$ sont alignés.

Exercice 21 : Parallélisme de droites et vecteurs directeurs

Dans le triangle $\text{ABC}$, $\text{I}$ est le milieu du segment $\text{[AC]}$ et les points $\text{D}$ et $\text{E}$ sont définis par $\overrightarrow{\text{AD}} = 3 \overrightarrow{\text{AB}}$ et $\overrightarrow{\text{BE}} = 2 \overrightarrow{\text{BC}}$.

Exprimer les vecteurs $\overrightarrow{\text{BI}}$ et $\overrightarrow{\text{DE}}$ comme une combinaison linéaire des vecteurs $\overrightarrow{\text{BA}}$ et $\overrightarrow{\text{BC}}$.
En déduire que $\overrightarrow{\text{BI}}$ est un vecteur directeur de $\text{(DE)}$.

Peut-on en déduire pour les droites $\text{(BI)}$ et $\text{(DE)}$ ?

Exercice 22 : Points alignés

Dans l'espace, on considère les points $\text{A}$, $\text{B}$, $\text{C}$ non alignés et $\text{D}$ et $\text{E}$ tels que $\overrightarrow{\text{AD}} = \dfrac{1}{2} \overrightarrow{\text{AB}} - \dfrac{2}{3} \overrightarrow{\text{BC}}$ et $\overrightarrow{\text{AE}} = x \overrightarrow{\text{AB}} + \overrightarrow{\text{BC}}$.

Déterminer la valeur du réel $x$ pour que les points $\text{A}$, $\text{D}$ et $\text{E}$ soient alignés.

Correction

A, D et E alignés $\iff \exists k \in \mathbb{R}$ tel que $\overrightarrow{AD}=k\overrightarrow{AE}$

$\iff \dfrac{1}{2} \overrightarrow{AB}-\dfrac{2}{3} \overrightarrow{BC} = k \left(x \overrightarrow{AB} + \overrightarrow{BC} \right) = kx \overrightarrow{AB} + k\overrightarrow{BC} \iff \left( \dfrac{1}{2}-kx \right)\overrightarrow{AB} + \left(-\dfrac{2}{3}-k\right) \overrightarrow{BC} =\vec{0} $

A, B, C ne sont pas alignés donc $\overrightarrow{AB}$ et $\overrightarrow{BC}$ ne sont pas colinéaires donc $\dfrac{1}{2}-kx=0$ et $-\dfrac{2}{3}-k=0$ donc $k=\dfrac{-2}{3}$ et $ \dfrac{1}{2}-\dfrac{-2}{3}x=0 \iff \dfrac{-2}{3}x=\dfrac{1}{2} \iff x = \dfrac{1}{2} \div \dfrac{-2}{3} =-\dfrac{1}{2} \times \dfrac{3}{2}=-\dfrac{3}{4}$

Pour $x=-\dfrac{3}{4}$, on a $\overrightarrow{AD}=\dfrac{1}{2} \overrightarrow{AB}-\dfrac{2}{3} \overrightarrow{BC}$ et $\overrightarrow{AE} = -\dfrac{3}{4} \overrightarrow{AB} + \overrightarrow{BC}$ donc $\overrightarrow{AD}=-\dfrac{2}{3}\overrightarrow{AE}$ donc les points A, D et E sont alignés.

Vecteurs coplanaires - bases des vecteurs de l'espace

Exercice 23

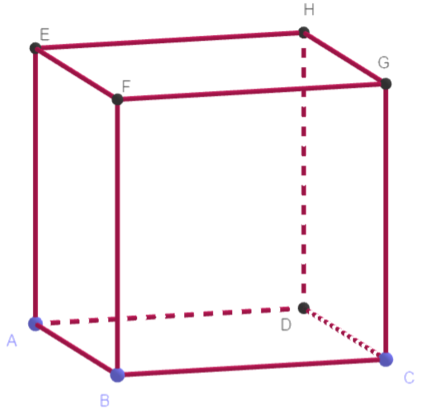
On considère la figure suivante.

Les vecteurs $\overrightarrow{\text{AE}}$, $\overrightarrow{\text{AG}}$ et $\overrightarrow{\text{EG}}$ sont-ils coplanaires ?
Démontrer que $\overrightarrow{\text{AB}}$, $\overrightarrow{\text{FH}}$ et $\overrightarrow{\text{EG}}$ sont coplanaires.
Démontrer que $\overrightarrow{\text{DH}}$, $\overrightarrow{\text{AH}}$ et $\overrightarrow{\text{FH}}$ forment une base.
Montrer que les points $\text{M}$,$\text{P}$ et un point quelconque $\text{Q}$ sont coplanaires.
Montrer que $\overrightarrow{\text{MN}}$, $\overrightarrow{\text{PB}}$ et $\overrightarrow{\text{AC}}$ sont coplanaires.
Montrer que $\overrightarrow{\text{NP}}$, $\overrightarrow{\text{BG}}$ et $\overrightarrow{\text{CD}}$ sont coplanaires.
Déterminer la décomposition des vecteurs ci-dessous dans la base $(\overrightarrow{\text{AB}},\overrightarrow{\text{AD}},\overrightarrow{\text{AE}})$

a) $\overrightarrow{\text{DG}}$

b) $\overrightarrow{\text{BH}}$

c) $\overrightarrow{\text{AG}}$

Correction 1-2-3-4

$\overrightarrow{AE}+\overrightarrow{EG}=\overrightarrow{AG}$ donc les vecteurs $\overrightarrow{AE}$, $\overrightarrow{AG}$ et $\overrightarrow{EG}$ sont coplanaires.
$\overrightarrow{AB}+\overrightarrow{EF}$ et les vecteurs $\overrightarrow{EF}$, $\overrightarrow{FH}$ et $\overrightarrow{EG}$ sont coplanaires donc les vecteurs $\overrightarrow{AB}$, $\overrightarrow{FH}$ et $\overrightarrow{EG}$ sont coplanaires
Les vecteurs $\overrightarrow{DH}$, $\overrightarrow{AH}$ et $\overrightarrow{FH}$ ne sont pas coplanaire donc ils forment une base.
$\overrightarrow{MN}= \overrightarrow{MD}+\overrightarrow{DH}+\overrightarrow{HN}=-\dfrac{1}{2} \overrightarrow{AB} +2 \overrightarrow{PB} -\dfrac{1}{2} \overrightarrow{BC} = 2 \overrightarrow{PB}-\dfrac{1}{2} \overrightarrow{AC}$ donc les vecteurs $\overrightarrow{MN}$, $\overrightarrow{PB}$ et $\overrightarrow{AC}$ sont coplanaires.

Exercice 24 : Bases des vecteurs de l'espace

Soit $({\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}})$ une base des vecteurs de l'espace et les vecteurs $\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ définis par :

$\overrightarrow{u} = \overrightarrow{i} -\overrightarrow{j} + \overrightarrow{k}$, $\overrightarrow{v} = 2 \overrightarrow{i} + \overrightarrow{k}$ et $\overrightarrow{w} = 3 \overrightarrow{i} - \overrightarrow{j}$.

Montrer que $\overrightarrow{u}$ et $\overrightarrow{v}$ ne sont pas colinéaires.
Peut-on trouver des réels $\text{A}$ et $\text{B}$ tels que $\overrightarrow{w} = a \overrightarrow{u} + b \overrightarrow{v}$ ?
Peut-on dire que $(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w})$ est une base ?

Exercice 25 : Points coplanaires ?

Soit un tétraèdre $\text{ABCD}$, $\text{I}$ le milieu de $\text{[AB]}$ et $\text{J}$ le milieu de $\text{[AC]}$.

On construit les points $\text{E}$ et $\text{F}$ tels que $\overrightarrow{\text{CE}} = \dfrac{1}{2} \overrightarrow{\text{BC}}$ et $\overrightarrow{\text{AF}} = \overrightarrow{\text{DE}}$.

Déterminer la nature des quadrilatères $\text{ECIJ}$ et $\text{ADEF}$.
Démontrer que $2\overrightarrow{\text{DJ}} - \overrightarrow{\text{DF}} = \overrightarrow{\text{JI}}$.
Que peut-on en déduire pour les vecteurs $\overrightarrow{\text{DI}}$, $\overrightarrow{\text{DJ}}$ et $\overrightarrow{\text{DF}}$ ?
Que peut-on en déduire pour les points $\text{D}$, $\text{I}$, $\text{J}$ et $\text{F}$ ?

Correction

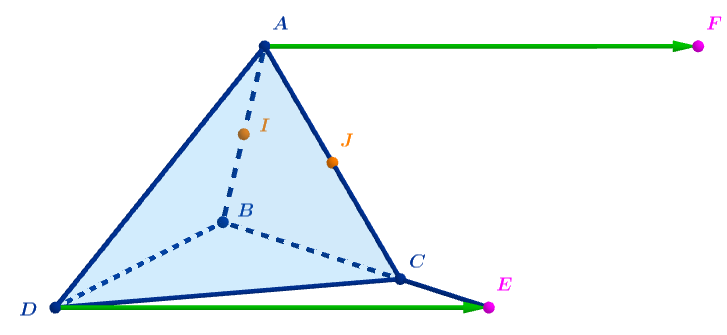
$\bullet$ $\overrightarrow{IJ}= \dfrac{1}{2}\overrightarrow{BC}=\overrightarrow{CE}$ donc le quadrilatère $\text{ECIJ}$ est un parallélogramme.

$\bullet$ $\overrightarrow{AF}=\overrightarrow{DE}$ donc le quadrilatère $\text{ADEF}$ est un parallélogramme.
$2\overrightarrow{DJ}-\overrightarrow{DF} = 2\overrightarrow{DJ}+\overrightarrow{FD} = 2\overrightarrow{DJ}+\overrightarrow{FJ} +\overrightarrow{JD} =\overrightarrow{DJ}+\overrightarrow{FJ}= \overrightarrow{DC}+\overrightarrow{CJ} + \overrightarrow{FA}+\overrightarrow{AJ}=\overrightarrow{DC}+\overrightarrow{ED}=\overrightarrow{EC}= \overrightarrow{JI}$
Comme $\overrightarrow{JI}$ peut s'exprimer en fonction des vecteurs $\overrightarrow{DJ}$ et $\overrightarrow{DF}$ alors les vecteurs $\overrightarrow{DI}$, $\overrightarrow{DJ}$ et $\overrightarrow{DF}$ sont coplanaires.
Les points D, I, J et F sont coplanaires.

Exercice 26 : Parallélisme de plans et vecteurs directeurs

Soit un tétraèdre $\text{ABCD}$ et les points $\text{E}$ et $\text{F}$ définis par :

$\overrightarrow{\text{BE}} = {\overrightarrow{\text{BA}} + \overrightarrow{\text{BC}} + \dfrac{1}{2} \overrightarrow{\text{CD}}}$ et $\overrightarrow{\text{DF}} = \overrightarrow{\text{DB}} + \overrightarrow{\text{DA}} + \dfrac{1}{2} \overrightarrow{\text{BC}}$

En exprimant $\overrightarrow{\text{AE}}$ et $\overrightarrow{\text{AF}}$ dans la base $(\overrightarrow{\text{BC}},\overrightarrow{\text{CD}})$, démontrer que $\text{A}$, $\text{E}$ et $\text{F}$ ne sont pas alignés.
Démontrer que les plans $\text{(BCD)}$ et $\text{(AEF)}$ sont parallèles.

Correction

$\overrightarrow{BE}=\overrightarrow{BA}+\overrightarrow{BC}+\dfrac{1}{2}\overrightarrow{CD}$ et $\overrightarrow{DF}=\overrightarrow{DB}+\overrightarrow{DA}+\dfrac{1}{2}\overrightarrow{BC}$

$\overrightarrow{AE}= \overrightarrow{AB}+\overrightarrow{BE}=\overrightarrow{AB}+ \overrightarrow{BA}+\overrightarrow{BC}+\dfrac{1}{2}\overrightarrow{CD} = \overrightarrow{BC}+\dfrac{1}{2}\overrightarrow{CD}$

$\overrightarrow{AF}= \overrightarrow{AD}+\overrightarrow{DF} =\overrightarrow{AD}+ \overrightarrow{DB}+\overrightarrow{DA}+\dfrac{1}{2}\overrightarrow{BC}=\overrightarrow{DB}+\dfrac{1}{2}\overrightarrow{BC} = \overrightarrow{DC}+\overrightarrow{CB}+\dfrac{1}{2}\overrightarrow{BC} = -\dfrac{1}{2}\overrightarrow{BC} -\overrightarrow{CD}$

$\overrightarrow{AE}$ et $\overrightarrow{AF}$ colinéaires $\iff \exists k \in \mathbb{R}$ tel que $\overrightarrow{AE}=k\overrightarrow{AF}$

$\iff \overrightarrow{BC}+\dfrac{1}{2}\overrightarrow{CD} = k \left( -\dfrac{1}{2}\overrightarrow{BC} -\overrightarrow{CD}\right) \iff \overrightarrow{BC}+\dfrac{1}{2}\overrightarrow{CD} = -\dfrac{k}{2}\overrightarrow{BC} -k\overrightarrow{CD} \iff \left( 1 + \dfrac{k}{2} \right) \overrightarrow{BC} + \left(\dfrac{1}{2}+k \right) \overrightarrow{CD}=\vec{0}$

Les vecteurs $\overrightarrow{BC}$ et $\overrightarrow{CD}$ ne sont pas colinéaires donc $\overrightarrow{AE}$ et $\overrightarrow{AF}$ colinéaires $\iff 1 + \dfrac{k}{2}$ et $\dfrac{1}{2}+k \iff k=-2$ et $k=-\dfrac{1}{2}$

Il n'existe donc pas de réel $k$ tel que $\overrightarrow{AE}=k\overrightarrow{AF}$ donc les points $\text{A}$, $\text{E}$ et $\text{F}$ ne sont pas alignés.
Les points $\text{A}$, $\text{E}$ et $\text{F}$ ne sont pas alignés donc $\left(\,\overrightarrow{AE}\,,\,\overrightarrow{AF}\,\right)$ est une base du plan $\text{(AEF)}$. $\overrightarrow{AE}$ et $\overrightarrow{AF}$ peuvent chacun s'exprimer en fonction de $\overrightarrow{BC}$ et $\overrightarrow{CD}$ donc $\left(\,\overrightarrow{BC}\,,\,\overrightarrow{CD}\,\right)$ est une base du plan $\text{(AEF)}$. Donc les plans $\text{(BCD)}$ et $\text{(AEF)}$ sont dirigés par un même couple de vecteurs donc ils sont parallèles.

Repères de l'espace

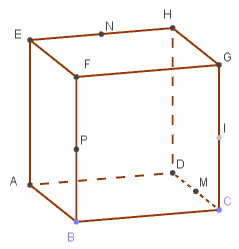
Dans les exercices 27 à 29, on considère la figure suivante.

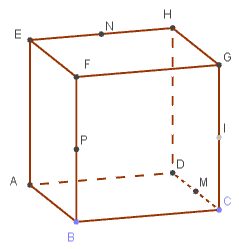
Exercice 27 : Calculs de coordonnées

Dans le cube ci-contre, $\text{M}$, $\text{N}$, $\text{P}$ et $\text{I}$ sont les milieux respectifs de $\text{[CD]}$, $\text{[EH]}$, $\text{[BF]}$ et $\text{[CG]}$.

On considère le repère $(\text{D};\overrightarrow{\text{DA}},\overrightarrow{\text{DC}},\overrightarrow{\text{DH}})$.

Dans chacun des cas suivants, déterminer les coordonnées :

Des points $\text{E}$, $\text{P}$, $\text{I}$ et $\text{B}$.
Des vecteurs $\overrightarrow{u} = \overrightarrow{\text{DA}}$, $\overrightarrow{v} = \overrightarrow{\text{IB}}$ et $\overrightarrow{w} = \overrightarrow{\text{BH}}$.
Du centre de la face $\text{EHDA}$.
Du centre $\Omega$ du cube.
Du vecteur $\overrightarrow{t} = 2 \overrightarrow{u} - 3 \overrightarrow{v}$ et du vecteur $\overrightarrow{p} = \overrightarrow{u} + \overrightarrow{v} + \overrightarrow{w}$

Exercice 28 : Milieux et points alignés

Déterminer les coordonnées des points $\text{S}$ et $\text{T}$ milieux respectifs des segments $\text{[NP]}$ et $\text{[HB]}$.

Les point $\text{S}$, $\text{T}$ et $\text{C}$ sont-ils alignés ?

Exercice 29 : Recherche des coordonnées d'un point

Déterminer les coordonnées du point $\text{Q}$ défini par $\overrightarrow{\text{QP}} + \overrightarrow{\text{QN}} = \overrightarrow{\text{BG}}$

Dans les exercices qui suivent, on considère un repère $(\text{O};\overrightarrow{i},\overrightarrow{j},\overrightarrow{k})$ de l'espace.

Exercice 30: Droite et plan parallèles ?

Soit les points $\text{A}(-2;2; - 1)$, $\text{B}(2;0;3)$, $\text{C}(-2;0;0)$, $\text{D}(0;-4;1)$ et $\text{E}(-2;-1;-2)$

Montrer que $\text{A}$, $\text{B}$ et $\text{C}$ définissent un plan.
Calculer les coordonnées du vecteur $\overrightarrow{\text{DE}}$ et celles du vecteur $- \overrightarrow{\text{AB}} - 2\overrightarrow{\text{AC}}$.
Que peut-on en déduire pour ces deux vecteurs et pour la droite $\text{(DE)}$ ?

Exercice 31 : Droite et plan parallèles ?

Soit les points $\text{A}(2;3;-1)$, $\text{B}(1;3;4)$, $\text{C}(0;1;-3)$ , $\text{D}(2;0;0)$ et $\text{E}(-2;-2;8)$ .

Montrer que $\text{A}$, $\text{B}$ et $\text{C}$ définissent un plan.
Peut-on trouver deux réels $x$ et $y$ tels que $\overrightarrow{\text{DE}} = x \overrightarrow{\text{AB}}+ y \overrightarrow{\text{AC}}$.
Que peut-on en déduire pour la droite $\text{(DE)}$ ?

Exercice 32 : Points coplanaires ?

Soit les points $\text{A}(0;1;-1)$, $\text{B}(2;1;0)$ , $\text{C}(-3;-1;1)$ et $\text{D}(7;3;-1)$.

Montrer que les points $\text{A}$, $\text{B}$ et $\text{C}$ ne sont pas alignés.
Calculer les coordonnées du vecteur $2 \overrightarrow{\text{AB}} - \overrightarrow{\text{AC}} - \overrightarrow{\text{AD}}$.
Que peut-on en déduire pour les points $\text{A}$, $\text{B}$ , $\text{C}$ et $\text{d}$ ?

Exercice 33 : Base des vecteurs de l'espace ?

Soit $\overrightarrow{u}\begin{pmatrix}-2\\3 \\-1\end{pmatrix}$, $\overrightarrow{v}\begin{pmatrix}1 \\-1\\-2\end{pmatrix}$ ,$\overrightarrow{w}\begin{pmatrix}4 \\-2\\-18\end{pmatrix}$ et $\overrightarrow{t}\begin{pmatrix}-3\\1 \\-1\end{pmatrix}$.

Peut-on trouver deux réels $x$ et $y$ tels que $\overrightarrow{w} = x \overrightarrow{u} + y \overrightarrow{v}$ ?
Montrer que les vecteurs $\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{t}$ sont linéairement indépendants.

Forment-ils une base des vecteurs de l'espace ?

Exercice 34 : Points coplanaires ?

Dans chacun des cas, étudier si les points sont coplanaires ou non.

$\text{A}(4;5;2)$ , $\text{B}(-3;-1;7)$, $\text{C}(9;5;-3)$ et $\text{D}(1;2;0)$.
$\text{A}(1;2;3)$ , $\text{B}(1;3;2)$, $\text{C}(2;1;3)$ et $\text{D}(2;3;1)$

Exercice 35 : Droites parallèles ou sécantes ?

Soit les points $\text{A}(2;1;5)$, $\text{B}(4;2;4)$ , $\text{C}(3;3;5)$ et $\text{D}(0;3;7)$.

Montrer que $\text{(AD)}$ et $\text{(BC)}$ sont parallèles.
Montrer que $\text{(AB)}$ et $\text{(CD)}$ sont sécantes.

\(\overrightarrow{\text{A...}} = \dfrac{1}{2} \overrightarrow{\text{AD}}\)	\(\overrightarrow{\text{B...}} = \overrightarrow{\text{BC}} + \overrightarrow{\text{BF}}\)	\(\overrightarrow{\text{B...}} = \dfrac{1}{2} \overrightarrow{\text{BC}} + \overrightarrow{\text{CG}}\)
\(\overrightarrow{\text{I...}} = - \overrightarrow{\text{IA}}\)	\(\overrightarrow{\text{...H}} = \overrightarrow{\text{BD}} + \overrightarrow{\text{BF}}\)	\(\overrightarrow{\text{A...}} = \dfrac{1}{2} \overrightarrow{\text{AD}} + \overrightarrow{\text{BF}} - \overrightarrow{\text{BA}}\)
\(\overrightarrow{\text{B...}} = 2 \overrightarrow{\text{EQ}}\)	\(\overrightarrow{\text{B...}} = \overrightarrow{\text{BA}} + \overrightarrow{\text{DH}}\)	\(\overrightarrow{\text{B...}} = \dfrac{1}{2}\overrightarrow{\text{BA}} + \overrightarrow{\text{BC}} + \overrightarrow{\text{BF}}\)
\(\overrightarrow{\text{H...}} = -2 \overrightarrow{\text{BI}}\)	\(\overrightarrow{\text{B...}} = \overrightarrow{\text{CK}} + \overrightarrow{\text{DH}}\)	\(\overrightarrow{\text{L...}} = \overrightarrow{\text{HG}} - \dfrac{1}{2} \overrightarrow{\text{AD}} + \overrightarrow{\text{CP}}\)