DROITES ET PLANS DE L'ESPACE
Avant tout, rappelons une propriété fondamentale :
Tout théorème de géométrie plane s'applique dans n'importe quel plan de l'espace.
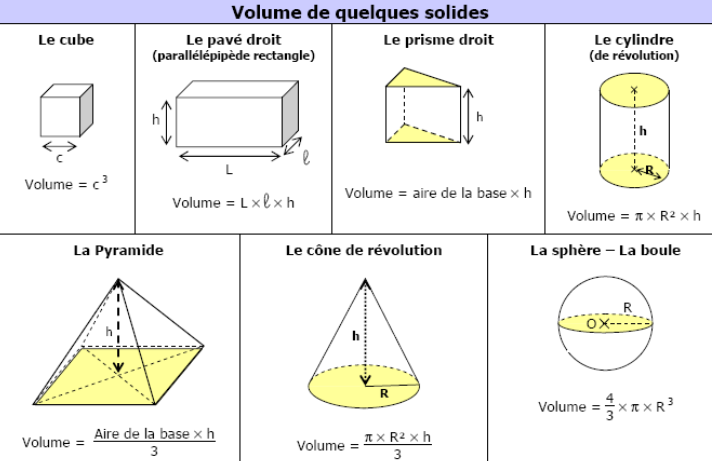
Les exemples de ce chapitre se réfèrent à la figure ci-dessous sur laquelle \(ABCDEFIJ\) est un cube et EGHJKLMN est un parallélépipède rectangle tel que \(HM=CI\) et \(JH=2JI\)
1 - POSITIONS RELATIVES DE DROITES ET DE PLANS
A - POSITIONS RELATIVES DE DEUX DROITES
-
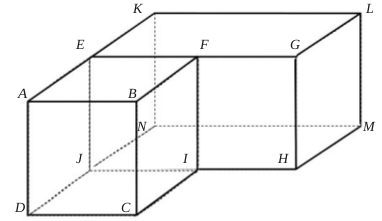
\(d\) et \(d'\) sont non coplanaires
Aucun plan ne les contient toutes les deux. Leur intersection est vide.
-
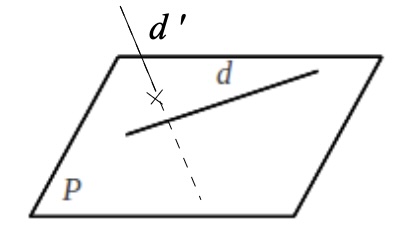
\(d\) et \(d'\) sont coplanaires
Elles sont sécantes. Elles ont un seul point en commun.
Elles sont parallèles. Elles sont strictement parallèles ou confondues.
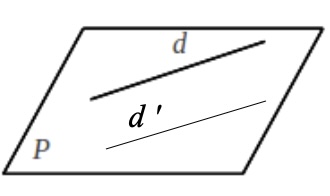
Exemple :
Les droites \(({AB})\) et \(({HN})\) sont non coplanaires.
Les droites \(({AB})\) et \(({JH})\) sont strictement parallèles.
Les droites \(({AL})\) et \(({KF})\) sont sécantes en \(F\) dans le plan \(({AKL})\)
B - POSITIONS RELATIVES DE DEUX PLANS
-
\(P_1\) et \(P_2\) sont parallèles
\(P_1\) et \(P_2\) sont confondus
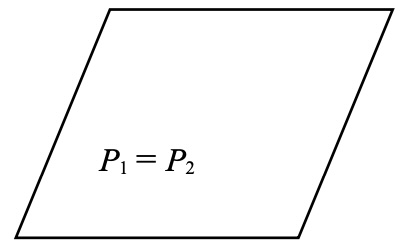
\(P_1\) et \(P_2\) sont strictement parallèles et ils n'admettent pas de points communs.
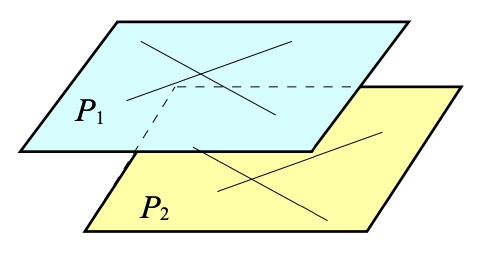
Il existe deux droites sécantes de \(P_1\) qui sont parallèles deux à deux à deux droites sécantes de \(P_2\)
-
\(P_1\) et \(P_2\) sont sécants non parallèles
Leur intersection est une droite.

Propriété d'incidence
Si deux plans sont parallèles, alors tout plan qui coupe l'un coupe l'autre et les intersections sont deux droites parallèles.
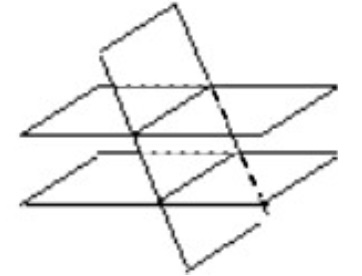
Exemple:
Les plans \(({EKL})\) et \(({EGJ})\) sont sécants suivant la droite \(({EG})\)
Les plans \(({EKL})\) et \(({JNM})\) sont strictement parallèles.
Le plan \(({CDEF})\) coupe les plans parallèles \(({AEJD})\) et \(({BFIC})\) suivant les droites parallèles \(({ED})\) et \(({FC})\).
C - POSITIONS RELATIVES D'UNE DROITE ET D'UN PLAN
-
\(d\) et \(P\) sont parallèles
\(d\) est contenue dans \(P\)
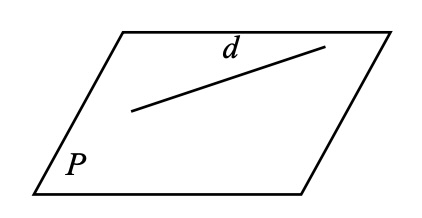
\(d\) est strictement parallèle à \(P\)
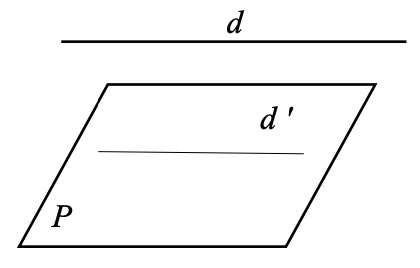
Une droite \(d\) est parallèle à un plan \(P\) si et seulement si il existe une droite \(d'\) contenue dans \(P'\) parallèle à P.
-
\(d\) et \(P\) sont sécants
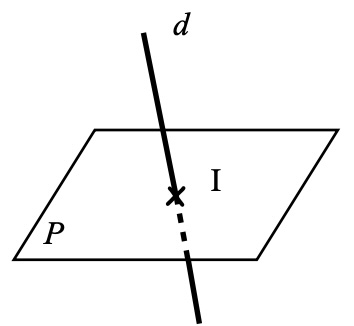
Leur intersection est un point unique.
Exemple :
La droite \(({ED})\) est parallèle à la droite \((FC)\) du plan \(({BFIC})\) . On en déduit que \(({ED})\) est parallèle au plan \(({BFIC})\).
2 - VECTEURS DE L'ESPACE
Comme dans le plan, à tout couple de points \(A\) et \(B\) de l'espace, on associe le vecteur \(\overrightarrow{{ AB }}\).
- Lorsque \(A \neq B\), la direction de \(\overrightarrow{{ AB }}\) est celle de la droite \(({AB})\) , le sens de \(\overrightarrow{{ AB }}\) est le sens de \(A\) vers \(B\) et la longueur ou norme de \(\overrightarrow{{ AB }}\), notée \(\left\| \overrightarrow{{ AB }} \right\|\) , est la distance \({AB}\).
Lorsque \(A = B\) , \(\overrightarrow{{ AA }}\) est le vecteur nul, noté \(\overrightarrow{0}\).
On désigne souvent les vecteurs par une seule lettre, par exemple \(\overrightarrow{u}\) , \(\overrightarrow{v}\) , \(\overrightarrow{w}\), ...
Pour tout point \(O\) de l'espace et pour tout vecteur \(\overrightarrow{u}\) , il existe un unique point \(\overrightarrow{M}\) tel que \(\overrightarrow{{ OM }} = \overrightarrow{u}\).
A - VECTEURS ÉGAUX
Chacune des propriétés suivantes signifie que les vecteurs non nuls \(\overrightarrow{{ AB }}\) et \(\overrightarrow{{ DC }}\) sont égaux :
\(\overrightarrow{{ AB }}\) et \(\overrightarrow{{ DC }}\) ont même direction, même sens et même norme.
\({ABCD}\) est un parallélogramme, c'est à dire \(\left\lbrack {AC} \right\rbrack\) et \(\left\lbrack {BD} \right\rbrack\) ont même milieu.
(Si \(A\), \(B\), \(C\) et \(D\) sont alignés, on dit que \({ABCD}\) est un parallélogramme aplati)
B - RÈGLES DE CALCUL
Les règles de calcul sur les vecteurs de l'espace sont analogues aux règles de calcul sur les vecteurs du plan.
RELATION DE CHASLES
Exemple : \({\overrightarrow{{ AB }} + \overrightarrow{{ BF }}} = \overrightarrow{{ AF }}\) \({\overrightarrow{{ AD }} + \overrightarrow{{ DI }}} = \overrightarrow{{ AI }}\) \({\overrightarrow{{ DE }} + \overrightarrow{{ KL }}} = \overrightarrow{{ DE }} + \overrightarrow{{ EG }} = \overrightarrow{{ DG }}\)
RÈGLE DU PARALLELOGRAMME
Exemple : \({\overrightarrow{{ DC }} + \overrightarrow{{ DJ }}} = {}\)\(\overrightarrow{{ DI }}\) \({\overrightarrow{{ JN }} + \overrightarrow{{ JH }}} = {}\)\(\overrightarrow{{ JM }}\) \({\overrightarrow{{ DC }} + \overrightarrow{{ DJ }} + \overrightarrow{{ DA }}} ={\overrightarrow{{ DI }} + \overrightarrow{{ DA }}} = \overrightarrow{{ DF }}\)
OPPOSÉ D'UN VECTEUR
Exemple : \(\overrightarrow{{ AB }} = -\overrightarrow{{ FE }}\)
MULTIPLICATION D'UN VECTEUR PAR UN RÉEL
Pour tous réels \(a\) et \(b\), et pour tous vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) on a :
\(a(\overrightarrow{u} + \overrightarrow{v}) = a\overrightarrow{u} + a\overrightarrow{v}\) , \((a + b)\overrightarrow{u} = a\overrightarrow{u} + b\overrightarrow{u}\) , \(a(b\overrightarrow{u}) = (ab)\overrightarrow{u}\) , \(a\overrightarrow{u} = \overrightarrow{0} \Leftrightarrow{} a = 0\) ou \(\overrightarrow{u} = \overrightarrow{0}\) etc ...
C - VECTEURS COLINÉAIRES
Deux vecteurs non nuls \(\overrightarrow{u}\) et \(\overrightarrow{v}\) qui ont la même direction sont dits colinéaires.
Par convention le vecteur nul est colinéaire à tout autre vecteur.
Dire que deux vecteurs non nuls \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont colinéaires revient à dire qu'il existe un réel \(k\) tel que \(\overrightarrow{u} = k \overrightarrow{v}\)
Dire que les points \(A\), \(B\) et \(C\) (distincts) sont alignés revient à dire qu'il existe \(k \in \mathbb{R}\) tel que \(\overrightarrow{{ AB }} = {k\overrightarrow{{ AC }}}\).
3 - INTERPRÉTATION VECTORIELLE DES DROITES ET PLANS DE L'ESPACE
A - DROITES
Définition
Soit \(d\) une droite. On appelle vecteurs directeurs de \(d\) les vecteurs, non nuls, définis par deux points de \(d\). Soit \(A\) un point de l'espace et \(\overrightarrow{u}\) un vecteur non nul.
\(({A;\overrightarrow{u}})\) représente la droite qui passe par \(A\) et de direction, la direction de \(\overrightarrow{u}\) .
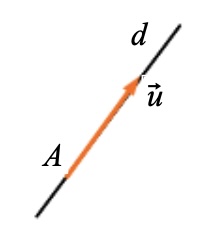
Remarques
La droite \((A;\overrightarrow{u})\) est l'ensemble des points \(M\) de l'espace tels que \(\overrightarrow{AM}\) et \(\overrightarrow{u}\) sont colinéaires, c'est à dire tels qu'il existe un réel \(k\) vérifiant \(\overrightarrow{AM} = k\overrightarrow{u}\).
Dire que les droites \((AB)\) et \((CD)\) sont parallèles revient à dire que les vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{CD}\) sont colinéaires, c'est à dire qu'il existe \(k \in \mathbb{R}^*\) tel que \(\overrightarrow{AB} = k \overrightarrow{CD}\).
Conséquence
Deux droites sont parallèles si, et seulement si, leurs vecteurs directeurs sont colinéaires.
B - PLANS
PLAN DÉTERMINÉ PAR TROIS POINTS
Propriété
Soit \(A\), \(B\) et \(C\) trois points non alignés.
Le plan \(({ABC})\) est l'ensemble des points \(M\) de l'espace tels qu'il existe des réels \(x\) et \(y\) vérifiant \(\overrightarrow{AM} = x \overrightarrow{AB} + y \overrightarrow{AC}\)
Preuve : non exigible
On pose \(\overrightarrow{u} = \overrightarrow{{ AB }}\) et \(\overrightarrow{v} = \overrightarrow{{ AC }}\)
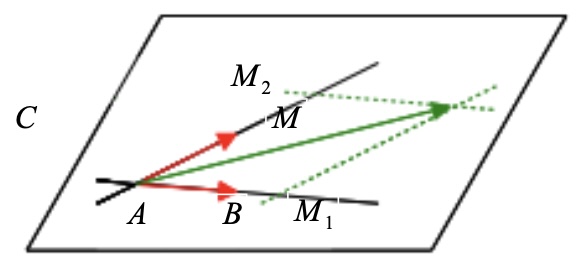
Le repère \(({A;\overrightarrow{u},\overrightarrow{v}})\) est un repère de \(({ABC})\). Ainsi, pour tout point \(M\) du plan, il existe un unique couple de réels \(({x;y})\) tels que \({\overrightarrow{AM} = x\overrightarrow{u} + y\overrightarrow{v}\)
Réciproquement, soit \(M\) un point de l'espace tel qu'il existe deux réels \(x\) et \(y\) vérifiant \({\overrightarrow{AM} = x\overrightarrow{u} + y\overrightarrow{v}\).
On note \(M_{1}\) et \(M_{2}\) les points définis par \(\overrightarrow{AM_1} = {x \overrightarrow{AB}}\) et \(\overrightarrow{AM_2} = y \overrightarrow{AC}\)
L'égalité \(\overrightarrow{AM_1} = x \overrightarrow{AB}\) prouve que \(M_{1}\) est sur \((AB)\) , donc dans le plan \((ABC)\). De même \(M_{2}\) est sur \((AC)\), donc dans le plan \((ABC)\) .
D'autre part on a \(\overrightarrow{AM} = \overrightarrow{AM_1} + \overrightarrow{AM_2}\), donc \(AM_1MM_2\) est un parallélogramme.
Les sommets \(A\), \(M_{1}\) et \(M_{2}\) sont dans le plan \((ABC)\), il en est donc de même pour le quatrième sommet \(M\).
Définition
On dit que les vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{AC}\) sont des vecteurs directeurs du plan \((ABC)\).
PLAN DÉFINI PAR UN POINT ET UN COUPLE DE VECTEURS NON COLINEAIRES
Un point \(A\) et deux vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) non colinéaires déterminent un unique plan : le plan \(({ABC})\) où \(\overrightarrow{{ AB }} = \overrightarrow{u}\) et \(\overrightarrow{{ AC }} = \overrightarrow{v}\) .
On note \(({A;\overrightarrow{u},\overrightarrow{v}})\) ce plan
\(({A;\overrightarrow{u},\overrightarrow{v}})\) est l'ensemble des points \(M\) de l'espace tels qu'il existe deux réels \(x\) et \(y\) vérifiant \(\overrightarrow{AM} = x \overrightarrow{u} + y \overrightarrow{v}\).
On dit que les vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont des vecteurs directeurs du plan \(({A;\overrightarrow{u},\overrightarrow{v}})\) ou encore que le plan \(({A;\overrightarrow{u},\overrightarrow{v}})\) est dirigé par \(\overrightarrow{u}\) et \(\overrightarrow{v}\).
Remarque :
Si \(\overrightarrow{u'}\) est un vecteur non nul colinéaire à \(\overrightarrow{u}\) , et \(\overrightarrow{v'}\) un vecteur non nul colinéaire à \(\overrightarrow{v}\) , alors le plan \(({A;\overrightarrow{u'},\overrightarrow{v'}})\) est le même que le plan \(({A;\overrightarrow{u},\overrightarrow{v}})\).
Exemple :
Les plans \(({A;\overrightarrow{{ DN }},\overrightarrow{{ KL }}})\) et \(({A;\overrightarrow{{ AE }},\overrightarrow{{ AB }}})\) sont confondus.
Conséquences :
-
Deux plans ayant même couple de vecteurs directeurs sont parallèles.
-
Une droite \(d\) et un plan \(P\) sont parallèles si, et seulement si, un vecteur directeur de \(d\) est un vecteur du plan \(P\).
4 - DÉCOMPOSITION DE VECTEURS
A - VECTEURS COPLANAIRES
Définition
Les vecteurs \(\overrightarrow{u}\), \(\overrightarrow{v}\), \(\overrightarrow{w}\), ..., de l'espace sont dits coplanaires lorsqu'un point \(O\) quelconque et les points \(A\), \(B,C\), ... , définis par \(\overrightarrow{{ OA }} = \overrightarrow{u}\), \(\overrightarrow{{ OB }} = \overrightarrow{v}\), \(\overrightarrow{{ OC }} = \overrightarrow{w}\), ..., sont coplanaires.
Remarques
-
Cette définition ne dépend pas du point \(O\) choisi.
-
Deux vecteurs sont toujours coplanaires.
-
Si deux vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont colinéaires, alors quel que soit le vecteur \(\overrightarrow{w}\) , les vecteurs \(\overrightarrow{u}\), \(\overrightarrow{v}\) et \(\overrightarrow{w}\) sont coplanaires.
Exemple : Montrer que les vecteurs \(\overrightarrow{{ HM }}\) , \(\overrightarrow{{ AL }}\) et \(\overrightarrow{{ DC }}\) sont coplanaires.
On a \(\overrightarrow{{ HM }} = \overrightarrow{{ AE }}\) et \(\overrightarrow{{ DC }} = \overrightarrow{{ AB }}\)
Les points \(A\), \(E\), \(B\) et \(L\) étant coplanaires, on en déduit que les vecteurs \(\overrightarrow{{ HM }}\), \(\overrightarrow{{ AL }}\) et \(\overrightarrow{{ DC }}\) sont coplanaires.
Propriété
\(\overrightarrow{u}\), \(\overrightarrow{v}\) et \(\overrightarrow{w}\) sont trois vecteurs de l'espace tels que \(\overrightarrow{u}\) et \(\overrightarrow{v}\) ne sont pas colinéaires. Dire que \(\overrightarrow{u}\), \(\overrightarrow{v}\) et \(\overrightarrow{w}\) sont coplanaires revient à dire qu'il existe des réels \(a\) et \(b\) tels que \(\overrightarrow{w} = a \overrightarrow{u} + b \overrightarrow{v}\).
Preuve : non exigible
Soit \(O\) un point de l'espace. On considère les points \(A\), \(B\) et \(C\) tels que \(\overrightarrow{{ OA }} = \overrightarrow{u}\) , \(\overrightarrow{{ OB }} = \overrightarrow{v}\) et \(\overrightarrow{{ OC }} = \overrightarrow{w}\).
\(\overrightarrow{u}\) et \(\overrightarrow{v}\) ne sont pas colinéaires, les points \(O\), \(A\) et \(B\) ne sont pas alignés et déterminent donc un plan, le plan \(({OAB})\).
Par définition, dire que \(\overrightarrow{u}\), \(\overrightarrow{v}\) et \(\overrightarrow{w}\) sont coplanaires revient à dire \(C \in (OAB)\) ... Ce qui revient à dire qu'il existe des réels \(a\) et \(b\) tels que \({\overrightarrow{OC} = a \overrightarrow{OA} + b \overrightarrow{OB}\).
Remarque
Si trois vecteurs sont non coplanaires, alors aucun des trois ne peut se décomposer en fonction des deux autres.
B - VECTEURS NON COPLANAIRES
Propriété
Soit \(\overrightarrow{u}\), \(\overrightarrow{v}\) et \(\overrightarrow{w}\) trois vecteurs non coplanaires de l'espace. Pour tout vecteur \(\overrightarrow{t}\) de l'espace, il existe un unique triplet \(({x;y;z})\) de réels tels que : \(\overrightarrow{t} = x\overrightarrow{u} + y\overrightarrow{v} + z\overrightarrow{w}\)
Preuve : non exigible
Existence :
Soit \(A,B,C,D\) et \(M\) des points tels que \(\overrightarrow{u} = \overrightarrow{{ AB }}\), \(\overrightarrow{v} = \overrightarrow{{ AC }}\), \(\overrightarrow{w} = \overrightarrow{{ AD }}\) et \(\overrightarrow{t} = \overrightarrow{AM}\).
\(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont non colinéaires, sinon \(\overrightarrow{u}\), \(\overrightarrow{v}\) et \(\overrightarrow{w}\) seraient coplanaires.
Ainsi \(A,B\) et \(C\) définissent un plan dont \(({A,{\overrightarrow{u},\overrightarrow{v}}})\) est un repère.
La parallèle à la droite \(({AD})\) passant par \(M\), dirigée par \(\overrightarrow{w}\), qui n'est pas un vecteur du plan \(({ABC})\), puisque \(\overrightarrow{u}\), \(\overrightarrow{v}\) et \(\overrightarrow{w}\) sont non coplanaires, est sécante à ce plan en un point \(H\).
\(\overrightarrow{{ HM }}\) et \(\overrightarrow{w}\) sont colinéaires, donc \(\overrightarrow{{ HM }} = {z\overrightarrow{w}}\), où \(z\) est un réel, et \(H\) appartient au plan \(({ABC})\), donc \(\overrightarrow{AH} = x \overrightarrow{u} + y \overrightarrow{v}\) ( \(x\) et \(y\) réels)
Comme \(\overrightarrow{t} = \overrightarrow{AM} = \overrightarrow{AH} + \overrightarrow{HM}\), on obtient l'existence d'un triplet \(({x;y;z})\) de réels tels que \(\overrightarrow{t} = x \overrightarrow{u} + y \overrightarrow{v} + z \overrightarrow{w}\)
Unicité :
On suppose que l'on a deux écritures : \(\overrightarrow{t} = x \overrightarrow{u} + y \overrightarrow{v} + z \overrightarrow{w} = x' \overrightarrow{u} + y' \overrightarrow{v} + z' \overrightarrow{w}\)
On a alors \((x - x') \overrightarrow{u} + (y - y') \overrightarrow{v} + (z - z') \overrightarrow{w}}} = \overrightarrow{0}}\).
Supposons que l'une des trois différences n'est pas nulle, par exemple \((z - z') \neq 0\).
On obtient :
\(\overrightarrow{w} = \dfrac{x - x'}{z - z'} \overrightarrow{u} + \dfrac{y - y'}{z - z'} \overrightarrow{v}\)
Les vecteurs \(\overrightarrow{u}\), \(\overrightarrow{v}\) et \(\overrightarrow{w}\) seraient alors coplanaires ... ce qui n'est pas possible.
On en déduit que \(z = z'\) et de la même façon que \(x = x'\) et \(y = y'\).
Remarque
On dit que l'on a décomposé le vecteur \(\overrightarrow{t}\) en fonction des vecteurs \(\overrightarrow{u}\), \(\overrightarrow{v}\) et \(\overrightarrow{w}\).
5 - REPÈRES DE L'ESPACE
Propriété et définitions :
Soit \(O\) un point et \(\overrightarrow{i}\),\(\overrightarrow{j}\) et \(\overrightarrow{k}\) trois vecteurs non coplanaires de l'espace.
À tout point \(M\) de l'espace, on peut associer un unique triplet de réels \(({x;y;z})\) tel que :
\(\overrightarrow{OM} = x \overrightarrow{i} + y \overrightarrow{j} + z \overrightarrow{k}\)
On dit que \(({x;y;z})\) sont les coordonnées du point \(M\) dans le repère \((O;\overrightarrow{i},\overrightarrow{j},\overrightarrow{k})\) ou que \(x\), \(y\) et \(z\) sont respectivement l'abscisse, l'ordonnée et la cote du point \(M\).
Exemple :
Dans le repère \((J;\overrightarrow{JD},\overrightarrow{JI},\overrightarrow{JE})\), on a \(D(1;0;0)\), \(K(-1;0;1)\) et \(L(-1;2;1)\)
Les propriétés et les règles de calcul vues dans le plan pour les coordonnées de vecteurs et de points se prolongent dans l'espace en ajoutant simplement une troisième coordonnée.
Propriétés
Dans un repère donné de l'espace, soit \(\overrightarrow{u}\begin{pmatrix}a \\b \\c\end{pmatrix}\) et \(\overrightarrow{u'}\begin{pmatrix}a' \\b' \\c'\end{pmatrix}\) deux vecteurs , \(A{({x;y;z})}\) et \(B{({x';y';z'})}\) deux points.
-
Le vecteur \(\overrightarrow{AB}\) a pour coordonnées \(\begin{pmatrix}x'-x \\y'-y \\z'-z\end{pmatrix}\).
-
Pour tout réel \(k\); le vecteur \(k\overrightarrow{u}\) a pour coordonnées \(\begin{pmatrix}ka \\kb \\kc\end{pmatrix}\).
-
Le vecteur \(\overrightarrow{u}+\overrightarrow{v}\) a pour coordonnées \(\begin{pmatrix}a+a'\\b+b'\\c+c'\end{pmatrix}\)
-
Le milieu \(I\) de \(\lbrack AB \rbrack\) a pour coordonnées \(\left(\dfrac{x+x'}2;\dfrac{y+y'}2;\dfrac{z+z'}2 \right)\)
-
\(\overrightarrow{u}=\overrightarrow{v}\) \(\Leftrightarrow \left\{ \begin{array}{c}a=a'\\b=b'\\c=c' \end{array}\right.\)
6 - RAPPELS SUR LES VOLUMES