Feuille d'exercices sur les limites de suites

Limites de suites : les différents cas possibles

Exercice 1: Vrai ou Faux

Si l'intervalle \(\rbrack{2,999;3,001}\lbrack\) contient tous les termes de la suite \((u_{n})\) à partir d'un certain rang alors \({\lim\limits_{n{\rightarrow + \infty}}u_{n}} = 3\).
S'il existe un intervalle ouvert ne contenant pas une infinité de termes de la suite \((u_{n})\), alors \((u_{n})\) ne converge pas vers \(L\).
Si tout intervalle de la forme \(\rbrack{\text{A}{; + \infty}}\lbrack\), où \(\text{A} \in {\mathbb{R}}\), contient au moins un terme \(u_{n}\) avec \(n \geqslant 100\), alors \((u_{n})\) tend vers +\(\infty\).
Si tout intervalle de la forme \(\rbrack{ {- \infty};\text{B}}\lbrack\), où \(\text{B} \in {\mathbb{R}}\), contient tous les termes de la suite \((u_{n})\) pour \(n \geqslant 100\), alors \((u_{n})\) tend vers \(-\infty\).
Si \((u_{n})\) prend un nombre fini de valeurs, alors \((u_{n})\) converge.
Une suite peut avoir plusieurs limites.
Si une suite ne converge pas, alors sa limite est +\(\infty\) ou -\(\infty\).

Exercice 2: Logique

Soit la proposition \((P_1)\) : « toute suite qui tend vers \(- \infty\) est majorée »

a. \((P_1)\) est-elle vraie ?

b. La réciproque de \((P1)\) est-elle vraie ?
Soit la proposition \((P_2)\) : « toute suite qui tend vers +\(\infty\) n'est pas majorée »

a. \((P_2)\) est-elle vraie ?

b. La réciproque de \((P_2)\) est-elle vraie ?

Exercice 3: Calculatrice

Soit \((s_n)\) la suite définie pour tout entier naturel \(n\) par \(s_n=-n^2+1000n\).

À l'aide de la calculatrice ou d'un tableur, afficher les 100 premiers termes de cette suite. Conjecturer le comportement de la suite \((s_n)\) quand \(n\) tend vers \(+\infty\).
Dresser le tableau de variation de la fonction \(f\) définie sur \(\mathbb{R}\) par \(f(x)=-x^2+ 1000x\).
Que penser de la conjecture établie à la question 1. ? Expliquer.

Exercice 4

Soit \((w_n)\) la suite définie pour tout entier naturel non nul par:

\[w_n=1+\dfrac{1}{n}\]

Déterminer à la calculatrice le premier entier \(N\) tel que \(w_N \in ]0,9;1,1[\)
Justifier que \(\lvert w_n-1\rvert<0,1\) si et seulement si \(w_n\) appartient à \(]0,9;1,1[\), puis résoudre, pour \(n\) entier naturel non nul, l'inéquation \(\lvert w_n-1 \rvert<0,1\).
Soit \(r\) un réel strictement positif.

a. Montrer qu'il existe un entier \(N\) tel que \(\lvert w_N-1 \rvert <r\).

b. Justifier alors que, pour tout \(n \geqslant N\) :

\[\lvert w_n- 1 \rvert <r\]

c. Que vient-on de démontrer?

Exercice 5: Suite positive à partir d'un certain rang

Montrer que toute suite qui converge vers 0,1 est strictement positive à partir d'un certain rang.

Opérations sur les limites

Exercice 6: Utiliser les opérations sur les limites

Étudier dans chaque cas la convergence de la suite \((u_{n})\).

\(u_{n} = { { {- 2}n^{2}} + \dfrac{\text{e}}{n}}\)
\(u_{n} = {300 - {n^{2}\sqrt{2}}}\)
\(u_{n} = { {({2 + \dfrac{3}{n}})}{({5 - \dfrac{1}{n^{3}}})}}\)
\(u_{n} = \dfrac{1}{ {({ {2n} + 1})}{({ { {- n}^2} - 9})}}\)
\(u_{n} = \dfrac{n + 2}{\dfrac{1}{\sqrt{n}} - 3}\)
\(u_{n} = \dfrac{2 + \dfrac{3}{n}}{5 - \dfrac{2}{n^{2}}}\)
\(u_{n} = \dfrac{5n^{2}}{10 - { {({2 + \dfrac{1}{n}})}{({5 + \dfrac{1}{n}})}}}\)

Exercice 7: Lever une indétermination

Étudier dans chaque cas la convergence de la suite \((u_{n})\).

\(u_{n} = {\dfrac{n^{5}}{5} - \dfrac{n^{2}}{2} - \text{e}}\)
\(u_{n} = { {\dfrac{1}{2}n^4} - {2n^{3}} + {5n^{2}} - \dfrac{1}{4}}\)
\(u_{n} = \dfrac{n^{2} - {3n} + 1}{n^{2} + 4}\)
\(u_{n} = \dfrac{9 - {n^2}}{ {({ {3n} + 2})}{({ {2n} + 1})}}\)
\(u_{n} = {\sqrt{n} - n}\)
\(u_{n} = \dfrac{\sqrt{n}}{n + \sqrt{n}}\)
\(u_{n} = {\sqrt{n + 1} - \sqrt{n}}\)

Exercice 8 : Trouver des suites

Dans chacun des cas suivant trouver deux suites \(u\) et \(v\) ayant pour limite \(+\infty\) telles que :

a. \({\lim\limits_{n{\rightarrow + \infty}}{({u_{n} - v_{n}})}} = {+ \infty}\)

b. \({\lim\limits_{n{\rightarrow + \infty}}{({u_{n} - v_{n}})}} = {- \infty}\)

c. \({\lim\limits_{n{\rightarrow + \infty}}{({u_{n} - v_{n}})}} = 1\)

d. \(u - v\) n'a pas de limite.
Dans chacun des cas suivant trouver deux suites \(u\) et \(v\) vérifiant \({\lim\limits_{n{\rightarrow + \infty}}u_{n}} = {+ \infty}\) et \({\lim\limits_{n{\rightarrow + \infty}}v}_{n} = 0\) , telles que :

a. \({\lim\limits_{n{\rightarrow + \infty}}{({u_{n}v_{n}})}} = {+ \infty}\)

b. \({\lim\limits_{n{\rightarrow + \infty}}{({u_{n}v_{n}})}} = 0\)

c. \({\lim\limits_{n{\rightarrow + \infty}}{({u_{n}v_{n}})}} = 1\)

d. \(uv\) n'a pas de limite.

Exercice 9: Raisonnement par l'absurde

Soit \((u_{n})\) et \((v_{n})\) deux suites définies sur \(\mathbb{N}\). On suppose que \((u_{n})\) est convergente et \((v_{n})\) est divergente . Soit \((w_{n})\) la suite définie par \(w_{n} = {u_{n} + v_{n}}\).

Montrer que la suite \((w_{n})\) est divergente.
Soit \((u_{n})\) la suite définie sur \(\mathbb{N}\) par \(u_{n} = { {({- 1})}^{n} + \dfrac{1}{n^{2} + 1}}\).

Démontrer que \((u_{n})\) est divergente.

Limites et comparaison

Exercice 10: Théorème de comparaison ou d'encadrement

Étudier dans chaque cas la convergence de la suite \((u_{n})\).

\(u_{n} = \dfrac{3\sin{(n)}}{n^{2}}\)
\(u_{n} = \dfrac{3 + {({- 1})}^{n}}{n^{2} + \sqrt{n}}\)
\(u_{n} = { {3{({- 1})}^{n}} + n}\)
\(u_{n} = {\dfrac{2\cos{(n)}}{n} + \dfrac{\sin{(n)}}{2n}}\)
\(u_{n} = \dfrac{ {5n} + {({- 1})}^{n + 1}}{ {2n} + {({- 1})}^{n}}\)
\(u_{n} = { {- {3n}^{3}} + {3\cos{(\dfrac{1}{n})}}}\)

Exercice 11: Avec la fonction exponentielle

On considère la suite \((u_{n})\) définie par \(u_{0} = \dfrac{1}{2}\) et, pour tout entier naturel \(n\), \(u_{n + 1} = \dfrac{\text{e}^{u_{n}}}{n + 2}\)

Montrer que, pour tout entier naturel \(n\), on a \(0 < u_{n} \leqslant 1\)
En déduire que, pour tout entier naturel \(n\), \(0 < u_{n + 1} \leqslant \dfrac{\text{e}}{n + 2}\)
Montrer que la suite \((u_{n})\) converge.

Exercice 12: Séries

Soit \((u_{n})\) la suite définie sur \({\mathbb{N}}^*\) par \(u_{n} = {\sum\limits_{k = 1}^{n}\dfrac{n}{n^{2} + k}}\)

a. Montrer que pour tout entier naturel \(n \in {\mathbb{N}}^*\),\(\dfrac{n^2}{n^{2} + n} \leqslant u_{n} \leqslant \dfrac{n^2}{n^{2} + 1}\)

b. Déterminer la limite de la suite \((u_{n})\).
Soit \((v_{n})\) la suite définie sur \({\mathbb{N}}^*\) par \(v_{n} = {\sum\limits_{k = 1}^{n}\dfrac{1}{\sqrt{n + k}}}\)

a. Montrer que pour tout entier naturel \(n \in {\mathbb{N}}^*\), \(v_{n} \geqslant \sqrt{\dfrac{n}{2}}\)

b. Déterminer la limite de la suite \((v_{n})\).

Limite d'une suite géométrique

Exercice 13

Étudier dans chaque cas la convergence de la suite \((u_{n})\).

\((u_{n})\) est une suite arithmétique de raison \(\dfrac{1}{4}\).
\(u_{n} = {1,00001^{n}}\)
\(u_{n} = {3 + {(\dfrac{11}{12})}^{n}}\)
\(u_{n} = {({- \dfrac{8}{5}})}^{n}\)
\(u_{n} = { {({- \dfrac{1}{7}})}^{n} + {(\dfrac{11}{12})}^{n}}\)
\(u_{n} = {\sum\limits_{k = 0}^{n}{(\dfrac{5}{4})}}^{k}\)
\(u_{n} = \dfrac{ {({- 1})}^{n}}{3^{n}}\)
\(u_{n} = \dfrac{\text{e}^{n} - 4^{n}}{4^{n} - 1}\)
\(u_{n} = \dfrac{2^{n + 1} + 5^{2n}}{5^{ {2n} - 3}}\)

Exercice 14: Nombre rationnel

Soit \((u_{n})\) la suite définie sur \({\mathbb{N}}^*\) par \(u_{n} = {3,777777}\)... (\(n\) chiffres 7). On a donc \(u_{1} = {3,7}\) , \(u_{2} = {3,77}\) ...

Montrer que la limite de \((u_{n})\) est un nombre rationnel.
Montrer que \(2,47474747...\) est un nombre rationnel.

Convergence de suites monotones

Exercice 15: Vrai ou faux

Si \((u_{n})\) converge vers \(\text{L}\) et si pour tout entier naturel \(n\), \(u_{n} > 2\), alors \(\text{L} > 2\).
Si \((u_{n})\) est une suite positive telle que, pour tout entier naturel \(n\), \(u_{n} \leqslant n\), alors la suite \((u_{n})\) converge.
Toute suite croissante et non majorée tend vers +\(\infty\).
Toute suite croissante et minorée est convergente.
Toute suite qui tend vers +\(\infty\) est croissante à partir d'un certain rang.
Toute suite décroissante et minorée par 0 a pour limite 0.
Toute suite convergente est monotone.
Toute suite qui converge vers 0 est soit croissante et négative, soit décroissante et positive.

Exercice 16: Étudier une suite monotone minorée

\((u_{n})\) est la suite définie par \(u_{0} = 10\) et, pour tout entier naturel \(n\), \(u_{n + 1} = { {\dfrac{2}{5}u_{n}} + 3}\).

Montrer que la suite est minorée par \(5\).
Montrer que \((u_{n})\) est décroissante.
En déduire que \((u_{n})\) est convergente et déterminer sa limite.

Exercice 17: Étudier une suite décroissante non minorée

\((u_{n})\) est la suite définie par \(u_{0} = 2\) et, pour tout entier naturel \({n,u_{n + 1}} = { {- {(u_{n})}^{2}} + u_{n} - 1}\).

Montrer que \((u_{n})\) est décroissante.
Montrer que \((u_{n})\) n'est pas minorée. (raisonnement par l'absurde)
En déduire la limite de la suite \((u_{n})\).

Exercice 18

\((u_{n})\) est la suite définie par \(u_{0} = 5\) et, pour tout entier naturel \(n\),\(u_{n + 1} = \sqrt{u_{n} + 12}\).

Étude de la convergence de \((u_{n})\).

a. Montrer que , pour tout entier naturel \(n\), \(u_{n} \geqslant 4\).

b. Montrer que \((u_{n})\) est décroissante.

c. Que peut-on déduire des questions précédentes ?
Détermination de la limite de \((u_{n})\).

a. Montrer que, pour tout entier naturel \(n\), \({u_{n + 1} - 4} \leqslant {\dfrac{1}{8}{({u_{n} - 4})}}\)

b. Montrer que, pour tout entier naturel \(n\), \(0 \leqslant {u_{n} - 4} \leqslant \dfrac{1}{8^{n}}\)

c. En déduire la limite de \((u_{n})\).

Exercice 19

On considère la suite \((u_{n})\) définie sur \({\mathbb{N}}^*\) par \(u_{n} = {n!}\).

Montrer que \((u_{n})\) est croissante.
Monter que \((u_{n})\) n'est pas majorée.
En déduire la limite de \((u_{n})\).

Algorithme - Python

Exercice 20: Méthode de Newton-Raphson

Introduction :

Dans un repère orthonormé \(({\text{O};\overrightarrow{\imath},\overrightarrow{\jmath}})\), on considère la fonction \(f\) définie par \({f{(x)}} = {x^{3} + {x - 3}}\) et sa courbe représentative \(\text{C}_{f}\) représentée ci-dessous.

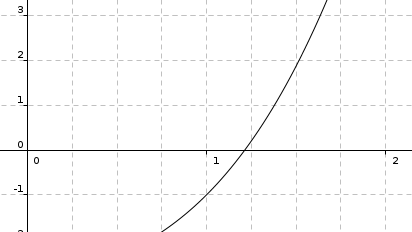
On constate que \(\text{C}_{f}\) coupe l'axe des abscisses en un unique point d'abscisse \(\alpha\) dont nous allons déterminer une valeur approchée.

a. Tracer la tangente \(\text{T}_{x_{0}}\) à \(\text{C}_{f}\) au point d'abscisse \(x_{0}\)=\(\dfrac{3}{2}\).

\(\text{T}_{x_{0}}\) coupe l'axe des abscisses en un unique point A .

Déterminer l'abscisse \(x_{1}\) de \(\text{A}\) .

b. Tracer la tangente \(\text{T}_{x_{1}}\) à \(\text{C}_{f}\) au point d'abscisse \(x_{1}\) . \(\text{T}_{x_{1}}\) coupe l'axe des abscisses en un unique point B d'abscisse \(x_{2}\). Que dire de \(x_{2}\) ?
Mise en place de l'algorithme :

Revenons sur le cas général.

Soit \(f\) une fonction dérivable sur \(\mathbb{R}\) telle que \({f{(x)}} = 0\) admette une unique solution \(\alpha\) sur \(\mathbb{R}\) et telle que la dérivée ne s'annule pas.

On note \(\text{C}_{f}\) sa courbe représentative et \(x_{0}\) un réel.

a. Déterminer l'équation de la tangente \(\text{T}_{x_{0}}\) à \(\text{C}_{f}\) au point d'abscisse \(x_{0}\).

b. Démontrer que l'abscisse \(x_{1}\) du point d'intersection \(\text{A}_{1}\) de \(\text{T}_{x_{0}}\) avec l'axe des abscisses vaut \(x_{1} = {x_{0} - \dfrac{f{(x_{0})}}{ {f'}{(x_{0})}}}\) .

On peut alors répéter ce procédé en remplaçant \(x_{0}\) par la nouvelle abscisse \(x_{1}\), et ainsi obtenir la suite \((x_{n})\) des réels \(x_{1}\), \(x_{2}\), \(x_{3}\) ... de plus en plus proche de \(\alpha\).

c. On s'intéresse à nouveau à la fonction \(f\) définie par \({f{(x)}} = {x^{3} + x - 3}\).

Compléter les pointillés dans le programme suivant écrit en Python pour qu'il affiche les valeurs la suite \((x_{n})\) jusqu'à \(n = 10\) .
```
from math import
N=int(input("N="))
x_0=float(input("x_0="))
def f(x):
return (..................)
def f_prime(x):
return (..................)
def MethodeNewton(x_0, N):
    x=..................
    for i in range(..................):
        x.append(.................)
        return x
    print(MethodeNewton(x_0,N))
```
Tester ce programme pour différente valeur de \(x_{0}\). Que constatez-vous ?

d. On se propose maintenant pour éviter les calculs inutiles de stopper le programme quand la différence entre deux termes consécutifs de la suite est inférieure à une précision \(p\).

Pour cela, compléter les pointillés dans le programme ci-dessous :
```
from math import *
x_0=float(input("x_0="))
p=float(input("p="))
def f(x):
    return (..................) 
def f_prime(x):
    return (..................)
def MethodeNewton(x_0,p):
    x=..................
    i=..................
    x.append(x[0] - f(x[0])/f_prime(x[0]))
    while (....................................>p):
    i=...............
    x.append(....................................)
    return x
print(MethodeNewton(x_0,p))
```
Application

Déterminer les fonctions à utiliser pour déterminer avec ce programme des valeurs approchées à \(10^{- 10}\) près de \(\pi\), \(\text{e}\), \(\sqrt{2}\) et du nombre d'or \(\dfrac{1 + \sqrt{5}}{2}\) (solution de \(x^{2} = {x + 1}\) ), puis déterminer ces valeurs approchées.

Attention :

Dans le cas où l'équation \({f{(x)}} = 0\) admet plusieurs solutions, il faut choisir une valeur de \(x_{0}\) proche de la solution attendue, afin que l'algorithme converge bien vers cette solution. Il faut aussi tout faire pour que la dérivée ne s'annule pas ...