Feuille d'exercices sur les suites - Rappels
Exercice 1. Définition de suites
Pour toutes les suites \((u_{n})\) définies ci-dessous, on demande de calculer \(u_{1}\), \(u_{2}\), \(u_{3}\) et \(u_{6}\).
-
\(u_{n} = \dfrac{7n-2}{n + 4}\)
-
\(\left\{ \begin{matrix}{ { u_{0} = 2}} \phantom{1111} \\ { {u_{n + 1} = {2{u_{n} + 3}}}} & \phantom{1} \end{matrix} \right.\)
-
\(u_{n}\) est le \(n\)-ième nombre premier.
-
\(u_{n}\) est la somme des \(n\) premiers nombres pairs strictement positifs.
-
\(u_{n}\) est le nombre de diviseurs positifs de \(n\).
-
Je place 1 000€ sur mon livret A au taux de 2.5% par an.
\(u_{n}\) est la somme dont je dispose la \(n\)-ième année.
-
\(u_{n}\) est la \(n\)-ième décimale du nombre \(\pi\).
Exercice 2 : Sens de variation d'une suite
Étudier le sens de variation des suites \((u_{n})\) définies ci-dessous :
-
\({u_{n} = 3}n-5\)
-
\({u_{n} = -}{n^{2} + 5}n-2\)
-
\(u_{n} = \dfrac{n + 1}{n + 2}\)
-
\(u_{n} = \dfrac{3^{n}}{2}\)
-
\(u_{n} = \sqrt{n^{2} + 3}\)
-
\(u_{n} = \left( {-\dfrac{1}{2}} \right)^{n}\)
-
\(\left\{ \begin{matrix}{ u_{0} = 0 \phantom{111}} \\ { {u_{n + 1} = {u_{n} + 3}}} \end{matrix} \right.\).
-
\(\left\{ \begin{matrix}{ u_{0} = 1} \phantom{1} \\ { {u_{n + 1} = {\dfrac{1}{2}u_{n}}}} \end{matrix} \right.\)
-
\(u_{n} = {\sqrt{n + 1} - \sqrt{n}}\) (plus difficile)
Exercice 3 : Majoration, minoration
-
Soit la suite \((u_{n})\) définie pour tout \(n\in \mathbb{N}^*\), par \({u_{n} = 5}-\dfrac{1}{n}\).
Montrer que la suite \((u_{n})\) est bornée.
-
Soit la suite \((u_{n})\) définie pour tout \(n\in \mathbb{N}^*\), par \(u_{n} = \dfrac{2{n + 1}}{n + 2}\).
a) Montrer que la suite \((u_{n})\) est majorée par 2.
b) Montrer que la suite \((u_{n})\) est minorée par \(\dfrac{1}{2}\).
-
Soit la suite \((u_{n})\) définie pour tout \(n\in \mathbb{N}^*\), par \({u_{n} = -}{n^{2} + 8}{n + 1}\).
Montrer que \((u_{n})\) est majorée par 17.
-
Soit la suite (un) définie pour tout \(n\in \mathbb{N}^*\), par \(u_{n} = {\sqrt{n + 1} - \sqrt{n}}\).
Montrer que \((u_{n})\) est majorée et minorée.
Exercice 4 : Représenter graphiquement une suite définie par récurrence
Dans chaque cas, on considère la fonction \(f\) telle que, pour tout entier naturel \(n\), \(u_{n + 1} = {f{(u_{n})}}\) . À l'aide de la droite \({d:y} = x\), représenter les premiers termes de la suite sur les axes, puis conjecturer le comportement de la suite (variations et limites éventuelles).
-
\(u_{0} = { {- 1},5}\) et \(u_{n + 1} = \sqrt{u_{n} + 2}\)
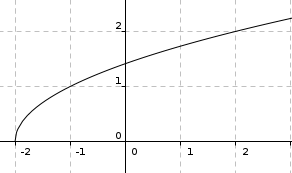
-
\(u_{0} = {1.5}\) et \(u_{n + 1} = { {2u_{n}} - 1}\)
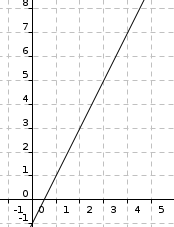
-
\(u_{0} = 2\) et \(u_{n + 1} = \dfrac{1}{u_{n} + 0.5}\)
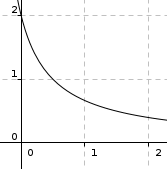
Exercice 5 : Suites arithmétiques
Les questions sont indépendantes.
-
On définit pour tout \(n\) la suite \((u_{n})\) par \({u_{n} = 3}n-2\).
Montrer que \((u_{n})\) est une suite arithmétique.
-
Soit \((u_{n})\) une suite arithmétique de premier terme \(u_{0} = 5\) et de raison \(\dfrac{1}{3}\).
Calculer le 9-ième terme, puis la somme \(\text{S} = {u_{0} + u_{1} + \ldots + u_{8}}\).
-
Soit \((v_{n})\) une suite arithmétique de premier terme \(u_{1} = 2\) et de raison \(-2\).
Calculer \(u_{15}\), puis la somme \(\Sigma = {u_{7} + u_{8} + \ldots + u_{15}}\).
-
Calculer : \(\text{S} = {11 + 14 + 17 + \ldots + 170 + 173}\).
Exercice 6 : Suites géométriques
Les questions sont indépendantes
-
Soit la suite \((u_{n})\) définie pour tout \(n \in \mathbb{N}^*\) par \(u_{n} = \dfrac{7^{n+1}}{5}\).
Montrer que \((u_{n})\) est une suite géométrique et déterminer sa raison et son premier terme.
-
Soit \((u_{n})\) une suite géométrique de premier terme \(u_{1} = \dfrac{1}{81}\) et de raison \(-3\).
Calculer \(u_{7}\), puis \(\text{S} = {u_{1} + u_{2} + \ldots + u_{7}}\).
-
Calculer \(\Sigma = 1 + 2 + 4 + 8 + \ldots + 4096\)
Les exercices qui suivent sont des extraits d'annales de bac. Il est très fréquent qu'un exercice sur les suites soit donné le jour du bac et une grande partie de leur étude a été faite en première, le sujet doit donc déjà être bien maîtrisé.
Exercice 7 : Suite "arithmético-géométrique"
Exercice très (très) classique que vous avez de fortes chances de retrouver (encore!) dans l'année.
On considère la suite \((u_{n})\) de nombres réels, définie pour tout entier \(n \geqslant 0\) par la relation de récurrence :
\({u_{n + 1} = \dfrac{1}{2}}{u_{n} + 3}\) et la relation initiale \(u_{0} = 2\).
-
Calculer \(u_{1}\),\(u_{2}\) et \(u_{3}\).
-
\((v_{n})\) est la suite définie pour tout entier naturel \(n\) par: \({v_{n} = u_{n}}-6\).
Démontrer que \((v_{n})\) est une suite géométrique et déterminer sa raison.
-
Pour tout entier naturel \(n\), exprimer \(v_{n}\) puis \(u_{n}\) en fonction de \(n\).
-
Calculer \(\text{S} = {v_{0} + v_{1} + \ldots + v_{9}}\) puis \(\text{S'} = {u_{0} + u_{1} + \ldots + u_{9}}\).
Exercice 8 : Augmentation de loyer
Une personne loue une maison à partir du premier janvier 1991. Elle a le choix entre deux formules de contrat. Dans les deux cas, le loyer annuel initial est de 4 800 € et le locataire s'engage à occuper la maison pendant 9 années complètes. Les valeurs décimales seront arrondies, si nécessaire, au centime près.
-
Contrat n°1 :
Le locataire accepte une augmentation annuelle de 5% du loyer de l'année précédente.
(a) Calculer le loyer \(u_{1}\) payé lors de la deuxième année.
(b) Exprimer \(u_{n}\) (loyer payé lors de la \(({n + 1})\)-ième année) en fonction de \(n\).
(c) Calculer \(u_{8}\).
(d) Calculer la somme payée à l'issue des 9 années de contrat.
-
Contrat n°2 :
Le locataire accepte une augmentation annuelle forfaitaire de 300 € du loyer de l'année précédente.
(a) Calculer le loyer \(v_{1}\) payé lors de la deuxième année.
(b) Exprimer \(v_{n}\) (loyer payé lors de la \(({n + 1})\)-ième année) en fonction de \(n\).
(c) Calculer la somme payée à l'issue des 9 années de contrat. Quel est le contrat le plus avantageux ?
Exercice 9 : Héritage
Bob a reçu \(200000\)€ en héritage. Il décide de placer cette somme et trouve un placement au taux de 6%. Mais chaque année il doit retirer \(9000\)€ pour payer les impôts dus à ce placement. On appelle \(\text{C}_{n}\) le capital acquis au bout de \(n\) années de placement.
-
Expliquer pourquoi \((\text{C}_{n})\) vérifie la relation de récurrence suivante : \({\text{C}_{n + 1} = 1.06}\text{C}_{n}-9000\)
-
Calculer à la calculatrice les premiers termes de cette suite. Est-elle arithmétique ? Géométrique ?
-
On considère la suite auxiliaire \((\text{U}_{n})\) définie par :
\[{\text{U}_{n} = \text{C}_{n}}-150000\] -
a) Montrer que \((\text{U}_{n})\) est une suite géométrique dont on précisera les caractéristiques.
b) Exprimer \(\text{U}_{n}\) puis \(\text{C}_{n}\) en fonction de \(n\).
c) De quelle somme, Bob disposera t-il au bout de 5 ans ?
d) Bob veut acheter une maison à \(280000\)€.
Combien d'années devra t-il attendre avant de disposer de cette somme ?
Exercice 10 : Suite auxiliaire
On considère la suite \(w_{n}\) définie par :
\(w_{n + 1} = \dfrac{w_{n}}{ {1 + 3}w_{n}}\) avec \(w_{0} = 1\)
-
Calculer \(w_{1}\), \(w_{2}\) et \(w_{3}\)
-
On considère la suite \((u_{n})\) définie pour tout \(n\) par :
\[u_{n} = \dfrac{1}{w_{n}}\]a) Démontrer que la suite \((u_{n})\) est arithmétique. Donner sa raison et son premier terme.
b) En déduire \(u_{n}\) en fonction de \(n\) puis \(w_{n}\) en fonction de \(n\).
c) Calculer alors \(w_{20}\).
Exercice 11 : Bac
L'objet de cet exercice est l'étude de la suite \((u_{n})\) définie par son premier terme \(u_{1} = \dfrac{3}{2}\) et la relation de récurrence:
Partie A - Algorithmique et conjectures
Pour calculer et afficher le terme \(u_9\) de la suite, un élève propose le programme en Python ci-dessous.
n=1
u=1.5
while n<9:
u=...
n=...
print(u)
-
Recopier et compléter les deux lignes de l'algorithme où figurent des points de suspension.
-
Comment faudrait-il modifier cet algorithme pour qu'il calcule et affiche tous les termes de la suite de \(u_{2}\) jusqu'à \(u_{9}\) ?
-
Avec cet algorithme modifié, on a obtenu les résultats suivants, arrondis au dix-millième :
\(n\) \(1\) \(2\) \(3\) \(4\) \(5\) \(6\) \(\ldots\) \(99\) \(100\) \(u_{n}\) 1,5 0,625 0,375 0,2656 0,2063 0,1693 \(\ldots\) 0,0102 0,0101 Au vu de ces résultats, conjecturer le sens de variation et la convergence de la suite \((u_{n})\).
Partie B - Étude mathématique
On définit une suite auxiliaire \((v_{n})\) par : pour tout entier \(n \geqslant 1\), \({v_{n} = n}{u_{n} - 1}\).
-
Montrer que la suite \((v_{n})\) est géométrique; préciser sa raison et son premier terme.
-
En déduire que, pour tout entier naturel \(n \geqslant 1\), on a:
\[u_{n} = \dfrac{1 + {(0,5)}^{n}}{n}\] -
Déterminer la limite de la suite \((u_{n})\).
-
Justifier que, pour tout entier \(n \geqslant 1\), on a:
\[{u_{n + 1} - u_{n}} = {- \dfrac{ {1 + {({ {1 + 0,5}n})}}{(0,5)}^{n}}{n{({n + 1})}}}\]En déduire le sens de variation de la suite \((u_{n})\).
Partie C - Retour à l'algorithmique
En s'inspirant de la partie A, écrire un algorithme permettant de déterminer et d'afficher le plus petit entier \(n\) tel que \(u_{n} < 0.001\).