Aller au contenu

Feuille d'exercices : Les fonctions sinus et cosinus

Fonctions paires, impaires et périodiques

Exercice 1 : Symétrie

En utilisant une symétrie éventuelle de la représentation graphique, indiquer si la fonction proposée est paire, impaire ou ni l'une ni l'autre.

\(f(x)=\sin x\) \(f(x)=\lvert x \rvert\cos x\)
\(f(x)=\cos x\) \(f(x)=\cos x\sin x\)
\(f(x)=e\cos x\) \(f(x)=\sin(x)\)
\(f(x)=\sin\bigl(\ln(x)\bigr)\) \(f(x)=\dfrac{\sin(x)}{\cos{x}}=\tan(x)\)
\(f(x)=\sin x+\dfrac{1}{x}\) \(f(x)=\cos x+\sin x\)

Exercice 2 : Compléter la courbe

La courbe \(C_f\) représentant la fonction \(f\), définie sur \([-8;8]\), est partiellement représentée ci-contre.

Sachant que \(f\) est impaire, compléter le tracé de \(C_f\).

Exercice 3 : Étudier la parité

Soit \(f\) la fonction définie sur \(\mathbb{R}\) par \(f(x)=\cos(2x)+3x^2\).

  1. Étudier la parité de \(f\).

  2. Que peut-on en déduire pour la courbe représentative de \(f\) dans un repère ?

Exercice 4 : Étudier la parité

Soit \(f\) la fonction définie sur \(\mathbb{R}\) par \(f(x)=x+\sin(x)\).

  1. Étudier la parité de \(f\).

  2. Que peut-on en déduire pour la courbe représentative de \(f\) dans un repère ?

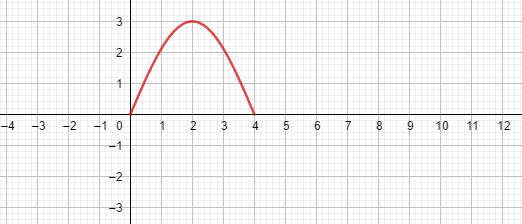
Exercice 5 : Étudier la parité et la périodicité – Compléter la courbe

Soit \(f\) la fonction définie sur \(\mathbb{R}\) par \(f(x)=3\sin\Bigl(\frac{\pi}{4}x\Bigr)\).

  1. Vérifier que la fonction \(f\) est périodique de période 8.

  2. Étudier la parité de \(f\).

  3. Quelles transformations permettent de tracer, dans un repère \((O;\vec{\imath},\vec{\jmath})\), la courbe représentative de \(f\) sur l'intervalle \([-4;12]\) à partir du tracé de \(f\) sur \([0;4]\) ?

En déduire le tracé de \(f\) sur \([-4;12]\).

Exercice 6 : Étudier la parité et la périodicité – Retrouver la courbe

  1. Pour chacune des fonctions définies sur \(\mathbb{R}\), étudier la parité et la périodicité :

    a. \(f_1(x)=\cos(2x)\)

    b. \(f_2(x)=2\sin(x)-1\)

    c. \(f_3(x)=\sin^2 x\)

    d. \(f_4(x)=\cos(x)\sin(x)\)

    e. \(f_5(x)=\cos^2 x\)

    f. \(f_6(x)=\dfrac{1}{2+\cos^2 x}\)

  2. En utilisant les résultats précédents, associer chaque fonction à sa représentation graphique.

\newpage

Quelques rappels de trigonométrie

Exercice 7 : Valeurs remarquables

Compléter le tableau ci-dessous :

\(x\) \(0\) \(\dfrac{\pi}{6}\) \(\dfrac{\pi}{4}\) \(\dfrac{\pi}{3}\) \(\dfrac{\pi}{2}\)
\(\sin x\)
\(\cos x\)

Exercice 8 : Formules à connaître et à retrouver

  1. Compléter : Pour tout \(x\in\mathbb{R}\), \(\cos^2(x)+\sin^2(x)=\;?\)

  2. En utilisant le cercle trigonométrique, compléter :

\(\cos(-x)=.........\) \(\sin(-x)=.........\) \(\cos(\pi-x)=.........\) \(\sin(\pi-x)=.........\)
\(\cos(\pi+x)=.........\) \(\sin(\pi+x)=.........\) \(\cos\Bigl(\dfrac{\pi}{2}-x\Bigr)=.........\) \(\cos\Bigl(\dfrac{\pi}{2}+x\Bigr)=.........\)
\(\sin\Bigl(\dfrac{\pi}{2}-x\Bigr)=.........\) \(\sin\Bigl(\dfrac{\pi}{2}+x\Bigr)=.........\)

Exercice 9 : Formules usuelles

On admet que \(\cos(a-b)=\cos a\cos b+\sin a\sin b\).

En utilisant ce résultat, associer les formules ci-dessous :

Formules d'addition :

\(\sin(a-b)\) \(\bullet\) \(\bullet\) \(\cos a\cos b-\sin a\sin b\)
\(\sin(a+b)\) \(\bullet\) \(\bullet\) \(\sin a\cos b-\sin b\cos a\)
\(\cos(a-b)\) \(\bullet\) \(\bullet\) \(\cos a\cos b+\sin a\sin b\)
\(\cos(a+b)\) \(\bullet\) \(\bullet\) \(\sin a\cos b+\sin b\cos a\)

En déduire les formules de duplication :

  • \(\sin(2a)=\; ?\)

  • \(\cos(2a)=\; ?\)

et les formules de linéarisation :

  • \(\cos^2(a)=\; ?\)

  • \(\sin^2(a)=\; ?\)

Équations et inéquations

Propriétés

\(\cos{x}=\cos{a} \Leftrightarrow x=a+2k\pi \; \text{ou}\; x=-a+2k\pi \quad k \in \mathbb{Z}\)

\(\sin{x}=\sin{a} \Leftrightarrow x=a+2k\pi \; \text{ou}\; x=\pi-a+2k\pi \quad k \in \mathbb{Z}\)

Exercice 10 : Déterminer les solutions réelles

Déterminer les solutions réelles des équations suivantes :

  1. \(\sin x=0\)

  2. \(\cos^2 x+\sin^2 x=1\)

  3. \(\cos x=-\dfrac{\sqrt{2}}{2}\)

  4. \(\sin x=-\dfrac{\sqrt{3}}{2}\)

  5. \(2\cos x=1\)

  6. \(\cos x+\sin x=7\)

  7. \(\cos x+3=2\)

  8. \(4\sin x=-2\)

Exercice 11 : Équations (à vérifier graphiquement avec la calculatrice)

RĂ©soudre dans \(\mathbb{R}\) les Ă©quations suivantes :

  1. \(\cos(2x)=\cos(3x-1)\)

  2. \(\sin(3x)=\sin(x+2)\)

  3. \(\cos(3x)=\sin(x)\)

Exercice 12 : Inéquations

Dans chacun des cas, dessiner en rouge sur un cercle trigonométrique l'ensemble des points associés à \(\alpha\), puis utiliser la représentation pour résoudre l'inéquation proposée dans l'intervalle donné.

  1. \(\cos(\alpha)<\dfrac{1}{2}\) avec \(\alpha\in\,]-\pi;\pi]\)

  2. \(\cos(\alpha)<\dfrac{1}{2}\) avec \(\alpha\in\,[0;2\pi[\)

  3. \(\sin(\alpha)<-\dfrac{\sqrt{3}}{2}\) avec \(\alpha\in\,]-\pi;\pi]\)

  4. \(\sin(\alpha)<-\dfrac{\sqrt{3}}{2}\) avec \(\alpha\in\,[0;2\pi[\)

Dérivées

Exercice 13

Dans chacun des cas, déterminer la dérivée de la fonction donnée :

  1. \(f(x)=3\cos x-5\sin x+x\)

  2. \(f(x)=3x\cos x\)

  3. \(f(x)=\sin x\cos x+\sin\Bigl(\frac{\pi}{7}\Bigr)\)

  4. \(f(t)=\cos^2 t\)

  5. \(f(t)=2\sin t\)

  6. \(f(p)=2p\cos p-\cos^3 p\)

Exercice 14 : Nombres dérivés et limites

DĂ©terminer les limites suivantes :

  • \(\displaystyle \lim_{x\to\pi}\dfrac{\sin x}{x-\pi}\)

  • \(\displaystyle \lim_{t\to 0}\dfrac{\sin t}{3t}\)

Primitives

Exercice 15

Dans chacun des cas, déterminer les primitives sur \(\mathbb{R}\) de la fonction donnée :

  1. \(f(x)=3\cos x-5\sin x+x\)

  2. \(f(x)=\sin x\cos x\)

  3. \(f(x)=\dfrac{1}{2}\cos^2 x\sin x\)

  4. \(f(x)=\sin x-\cos\Bigl(\dfrac{\pi}{9}\Bigr)\)

  5. \(f(x)=\dfrac{\cos x}{\sin x-3}\)

  6. \(f(x)=\dfrac{2\cos x}{(\sin x+3)^2}\)

Exercice 16 : Avec des fonctions auxiliaires

  1. Déterminer les dérivées des fonctions \(g\) et \(h\) définies par :

  2. \(g(x)=x^2\sin x\)

  3. \(h(x)=-2x\cos x\)

  4. Déterminer la dérivée de la fonction \(u=g-h\).

  5. En déduire les primitives sur \(\mathbb{R}\) de la fonction \(f\) définie par \(f(x)=x^2\cos x\).

Variations

Exercice 17 : Variations de fonctions sans calculer la dérivée

  1. Déterminer les variations de la fonction \(f\) définie par \(f(x)=5-2\sin x\) sur \(\left[-\dfrac{\pi}{2};\dfrac{\pi}{2}\right]\).

  2. Déterminer les variations de la fonction \(g\) définie par \(g(x)=2\cos x-1\) sur \([-\pi;\pi]\).

Exercice 18 : Encadrements

  1. Dans chacun des cas, encadrer \(\cos a\) :

a. \(\dfrac{\pi}{3}\leqslant a \leqslant \dfrac{5\pi}{6}\)

b. \(-\dfrac{3\pi}{4}\leqslant a \leqslant 0\)

  1. Dans chacun des cas, encadrer \(\sin a\) :

a. \(-\dfrac{\pi}{2}\leqslant a \leqslant \dfrac{\pi}{3}\)

b. \(\dfrac{3\pi}{4}\leqslant a \leqslant \dfrac{5\pi}{4}\)

Exercice 19 : Variations de fonctions en calculant la dérivée

Pour chacun des cas, déterminer les variations de la fonction \(f\) sur l'intervalle \(I\) donné :

  1. \(f(x)=2\cos x+5x-5\) sur \(I=\mathbb{R}\)

  2. \(f(x)=2-4x+4\sin x\) sur \(I=[0;\pi]\)

  3. \(f(x)=\sin x\cos x\) sur \(I=\Bigl[0;\dfrac{\pi}{4}\Bigr]\)

Exercice 20 : Théorèmes de comparaison

Soit la fonction \(f\) définie sur \(\mathbb{R}\) par \(f(x)=x-3\cos x+1\).

  1. Montrer que pour tout réel \(x\), \(x-2\leqslant f(x)\leqslant x+4\).

  2. RĂ©soudre les Ă©quations \(f(x)=x-2\) et \(f(x)=x+4\).

  3. Interpréter graphiquement les résultats des questions 1 et 2.

  4. DĂ©terminer les limites de \(f\) en \(+\infty\) et en \(-\infty\).

  5. La fonction \(f\) est-elle bornée ?

  6. Étudier les variations de \(f\) sur \([-\pi;\pi]\) et en déduire celles de \(f\) sur \(\mathbb{R}\).

Courbes et représentations graphiques

Exercice 21 : Identifier les courbes

Identifier les courbes de chacune des fonctions.

Exercice 22 : RĂ©solutions graphiques d'Ă©quations

RĂ©soudre graphiquement dans \(\mathbb{R}\) les Ă©quations suivantes :

a. \(\cos x=1\) b. \(\sin x=1\) c. \(\cos x=0\)
d. \(\sin x=0\) e. \(\cos x=\sin x\) f. \(\sin x=x\)

Exercice 23 : La courbe de la fonction sinus et la droite d'Ă©quation \(y=x\)

Soit \(C\) la courbe de la fonction sinus et \(T\) la tangente Ă  \(C\) au point d'abscisse 0.

  1. DĂ©terminer une Ă©quation de \(T\).

  2. Étudier les variations de la fonction \(f\) définie sur \(\mathbb{R}\) par \(f(x)=\sin x-x\).

  3. Calculer \(f(0)\) et en déduire la position de \(T\) par rapport à \(C\).

Autres fonctions trigonométriques

Exercice 24

  1. Encadrer \(f(x)=2\sin\Bigl(4x-\dfrac{\pi}{6}\Bigr)\) et résoudre dans \(\mathbb{R}\) l'équation \(f(x)=0\).

  2. Dans chaque cas, montrer que \(f\) est de signe constant :

    a. \(f(x)=\cos(3x)+2\)

    b. \(f(x)=5-3\sin\Bigl(2x-\dfrac{\pi}{8}\Bigr)\)

Exercice 25

Soit \(f\) la fonction définie sur \(\mathbb{R}\) par \(f(x)=\frac{3}{4}\cos\Bigl(3x+\dfrac{\pi}{6}\Bigr)\).

  1. Étudier la parité de \(f\).

  2. Démontrer que \(f\) est périodique de période \(\dfrac{2\pi}{3}\).

  3. RĂ©soudre dans \(\mathbb{R}\) l'Ă©quation \(f'(x)=0\).

  4. Établir le tableau de variation de \(f\) sur \(\left[0;\dfrac{2\pi}{3}\right]\).

Exercice 26 : La fonction tangente

Soit \(f\) la fonction définie par \(f(x)=\dfrac{\sin x}{\cos x}\).

  1. Déterminer l'ensemble de définition de \(f\).

  2. \(f\) est-elle paire ? Impaire ? Ni l'un ni l'autre ?

  3. Démontrer que \(f\) est périodique de période \(\pi\).

  4. Représenter graphiquement \(f\) à l'aide de la calculatrice.

Exercice 27 : Limites et théorèmes de comparaison

  1. Conjecturer les limites suivantes Ă  l'aide de l'outil de votre choix :

    a. \(\displaystyle \lim_{x\to+\infty}\Bigl(3\sin x+4x-5\Bigr)\)

    b. \(\displaystyle \lim_{x\to+\infty}\frac{2\sin x}{x+1}\)

    c. \(\displaystyle \lim_{x\to+\infty}\frac{x\cos x}{9-x^2}\)

  2. Justifier les limites précédentes.

Exercice 28 : Avec une suite

Soit \(f\) la fonction définie sur \(\mathbb{R}^+\) par \(f(x)=x-\dfrac{\pi}{5}\cos(2\pi x)\)

et \((u_n)\) la suite définie sur \(\mathbb{N}\) par \(u_n=f(n)\).

  1. Prouver que la suite \((u_n)\) est croissante.

  2. La fonction \(f\) est-elle croissante sur \(\mathbb{R}^+\) ?

Vu au bac

Exercice 29 (sujet 0)

  1. Sur l'intervalle \([0~;~2 \pi]\), l'Ă©quation \(\sin (x) = 0,1\) admet :

a. zéro solution b. une solution c. deux solutions d. quatre solutions

  1. On considère la fonction \(f\) définie sur l'intervalle \([0~;~\pi]\) par \(f(x) = x + \sin (x).\) On admet que \(f\) est deux fois dérivable.

a. La fonction \(f\) est convexe sur l'intervalle \([0~;~\pi]\).

b. La fonction \(f\) est concave sur l'intervalle \([0~;~\pi]\).

c. La fonction \(f\) admet sur l'intervalle \([0~;~\pi]\) un unique point d'inflexion.

d. La fonction \(f\) admet sur l'intervalle \([0~;~\pi]\) exactement deux points d'inflexion.

Exercice 30 (sujet Centres Étrangers J1 2024)

On considère l'équation différentielle \(\left(E_0\right) :\quad y' = y\) où \(y\) est une fonction dérivable de la variable réelle \(x\).

  1. Démontrer que l'unique fonction constante solution de l'équation différentielle \(\left(E_0\right)\) est la fonction nulle.

  2. Déterminer toutes les solutions de l'équation différentielle \(\left(E_0\right)\).

On considère l'équation différentielle \((E) :\quad y' = y - \cos (x) - 3\sin (x)\) où \(y\) est une fonction dérivable de la variable réelle \(x\).

  1. La fonction \(h\) est définie sur \(\mathbb{R}\) par \(h(x) = 2 \cos (x) + \sin (x)\).

On admet qu'elle est dérivable sur \(\mathbb{R}\).

Démontrer que la fonction \(h\) est solution de l'équation différentielle \((E)\).

  1. On considère une fonction \(f\) définie et dérivable sur \(\mathbb{R}\).

DĂ©montrer que : \(f\) est solution de \((E)\) est Ă©quivalent Ă  \(f - h\) est solution de \(\left(E_0\right)\).

  1. En déduire toutes les solutions de l'équation différentielle \((E)\).

  2. Déterminer l'unique solution \(g\) de l'équation différentielle \((E)\) telle que \(g(0) = 0\).