Feuille d'exercices sur le logarithme

Définition - propriétés algébriques

Exercice 1 : QCM

Plusieurs réponses sont possibles.

Équations ...

a. \(e^{3}\) est la solution de l'équation \(\ln x = 3\)

b. \(e^{-3}\) est la solution de l'équation \(\ln x = -3\)

c. \(\ln(3)\) est la solution de l'équation \(e^x = 3\)

d. \(\ln(- 3)\) est la solution de l'équation \(e^x = -3\)

e. \({- \ln}3\) est la solution de l'équation \(e^x = \dfrac{1}{3}\)

f. L'équation \({\ln x} = m\) où \(m \in \mathbb{R}\), admet toujours une unique solution \(x = e^m\)

g. L'équation \(e^x = m\) où \(m \in \mathbb{R}\), admet toujours une unique solution \(x = \ln m\)
Formules

a. \(\ln(a + b) = \ln(a) \times \ln(b)\) b. \(\ln(ab) = \ln(a)\ln(b)\)

c. \(\ln(a - b) = \dfrac{\ln(a)}{\ln(b)}\) d. \(\ln{\left(\dfrac{a}{b}\right)} = \ln(a)-\ln(b)\)
\(\ln{({ab}^5)} = ...\)

a. \(5\ln(ab)\) b. \(5(\ln(a) + \ln(b))\)

c. \(5\ln(a)\ln(b)\) d. \(\ln(a) + 5\ln(b)\)
\(\ln \left(a \times \dfrac{1}{a}\right) = ...\)

a. \(-(\ln(a))^2\) b. \(-1\)

c. \({-2}\ln(a)\) d. \(0\)
la moitié de \(\ln(a)\) est ...

a. \(\ln(a) - \ln(2)\) b. \(\ln(a^{-2})\)

c. \(\ln(\sqrt{a})\) d. \(\sqrt{\ln(a)}\)

Exercice 2 : Calculs avec les formules

\(\text{Simplifier :}\)
1. \(e^{\ln(2)} - e^{\ln(7)}\)	2. \(3e^{\ln(5)} + 5e^{-\ln(3)}\)	3. \(\ln(2\sqrt{3}) + 2\ln(\sqrt{3})\)
4. \(\ln \left(\dfrac{3e^2}{\sqrt{e}}\right)\)	5. \(\dfrac{\ln(125)}{\ln(25)}\)	6. \(\dfrac{(\ln(e^3))^2}{\ln(e^4)}\)
7. \(\ln(1 + e^x) - x - \ln(1 + e^{-x})\)

Exercice 3 : Équations et inéquations

Résoudre les équations et inéquations ci-dessous :

\((e^x - 2)(e^{2x} - 8) = 0\)
\((e^{x-1}-3)^2 = 0\)
\((e^{x^2+{2x}+5} + e^{-x})(3e^x + 4)= e\)
\(8 - 4e^{\ln(0,5) \times x + 1} > 0\)
\(e^{3x + 5} < 3e^x\)
\((2e^x - 10)(5 - e^x) < 0\)

Exercice 4

Compléter ...

La courbe représentative de la fonction exponentielle passe par le point \(A(\ln2 ; ... )\) et \(B( ... ; \pi )\)
L'ensemble des réels \(x\) tels que \(\ln(x) \leqslant 0\) est ...
Si \(e^a = b\), \((b > 0)\) , alors \(\ln( ... ) = ...\)
\(\forall x \in ...\) , \(\ln(e^x) = x\)
\(\forall x \in ...\) , \(e^{\ln(x)} = x\)
\(\forall x \in ...\) , \(\ln(x) > 0\)

Exercice 5 : Calculs

Exprimer en fonction de \(\ln 2\) et de \(\ln 3\) :

a. \(\ln \left(\dfrac{8}{9}\right)\)

b. \(\ln\left(\dfrac{4\sqrt{2}}{27}\right)\)

c. \(\dfrac{\ln{64}}{\ln{81}} + \dfrac{\ln{49}}{\ln 7}\)
Simplifier :

a. \(4\ln(e^2) + \ln(\sqrt{e})\)

b. \(\ln\left(\dfrac{\sqrt{e}}{e^3}\right)\)

c. \(\dfrac{\ln(e^4)}{(\ln(e^3))^2}\)
Calculer :

a. \(\ln {3} + \ln {9} + \ln {27}\)

b. \(\ln(\sqrt{5} - 2) + \ln(\sqrt{5} + 2)\)

Exercice 6 : Vrai ou faux

Justifier

\(\forall x \in \mathbb{R}^*\), \(\ln(x^3) = 3\ln(x)\)
\(\forall x \in \mathbb{R}\), \(\ln(1 + e^x) = x + \ln(1 + e^{- x})\)
\(\forall x \in \mathbb{R}\), \(\ln(1 + e^{8x}) - 4x = \ln \left(e^{4x} + e^{-4x}\right)\)

Étude de la fonction logarithme népérien

Exercice 7 : QCM

Plusieurs réponses sont possibles.

L'ensemble de définition de la fonction \(\ln\) est :

a. \(\lbrack 1; + \infty \lbrack\)

b. \(\mathbb{R}^+\)

c. \(\mathbb{R}\)

d. \(\mathbb{R}^-\)

e. \(\mathbb{R}^{+*}\)

f. \(\rbrack 0; + \infty \lbrack\)
La fonction \(\ln\) :

a. est strictement positive sur \(\mathbb{R}^{+*}\).

b. est strictement croissante sur \(\mathbb{R}^{+*}\).

c. est strictement positive sur \(\rbrack 1, +\infty \lbrack\).

d. est égale à sa dérivée.

e. prend la valeur \(1\) en \(0\).
Soit \(\text{C}\) la courbe représentative de la fonction \(\ln\).

a. La droite \(\Delta : y = 0\) est une asymptote à \(\text{C}\).

b. \(\text{C}\) coupe l'axe des abscisses.

c. \(\text{C}\) admet une tangente de coefficient directeur \(-2\).

d. \(\text{C}\) et la courbe de la fonction exp sont symétriques par rapport à la droite d'équation \(d : y = x\).

Exercice 8 : Limites

Associer chaque limite au résultat qui convient :


\(\lim\limits_{x \to +\infty}\ln x \quad \bullet\)		\(\bullet \quad 1\)
\(\lim\limits_{x \to 0^+}x^{n}\text{ln}x, n \in \mathbb{N}^* \quad \bullet\)		\(\bullet \quad +\infty\)
\(\lim\limits_{x \to 0^+}\ln x \quad \bullet\)		\(\bullet \quad 0\)
\(\lim\limits_{x \to 0}\dfrac{\ln({1 + x})}{x} \quad \bullet\)		\(\bullet \quad\) n'existe pas
\(\lim\limits_{x \to 0^+}\dfrac{\ln(x)}{x} \quad \bullet\)		\(\bullet -\infty\)
\(\lim\limits_{x \to +\infty}\dfrac{\ln x}{x^n}, n \in \mathbb{N}^* \quad \bullet\)		\(\bullet \quad -1\)

Exercice 9 : Déterminer une limite

Déterminer les limites suivantes


1. \(\lim\limits_{x \to 0^+} \left( \dfrac{3}{x} - 4x - {3x^2\ln x} \right)\)	2. \(\lim\limits_{x \to +\infty} \left( 4x^{3} - \dfrac{5\ln x}{x^5} \right)\)	3. \(\lim\limits_{x \to 0^+} \left( x\ln x - \dfrac{1}{\ln x} \right)\)
4. \(\lim\limits_{x \to 1^-} \left( {\ln x} - \dfrac{1}{\ln x} \right)\)	5. \(\lim\limits_{x \to +\infty} \left( \ln x - \dfrac{1}{\ln x} \right)\)	6. \(\lim\limits_{x \to 0^+} (2x + \ln x)^2\)
7. \(\lim\limits_{x \to -\infty} \ln(3 - e^x)\)	8. \(\lim\limits_{x \to \ln{3}^-} \ln(3 - e^x)\)	9. \(\lim\limits_{x \to 1^+} \left( \ln(x - 1) \ln \left( 2 - \dfrac{1}{x} \right) \right)\)
10. \(\lim\limits_{x \to +\infty} \left( \ln(x - 1) \left( \ln 2 - \dfrac{1}{x} \right) \right)\)	11. \(\lim\limits_{x \to +\infty} \ln{ \left( \dfrac{3x - 6}{7x} \right)}\)	12. \(\lim\limits_{x \to 2^+} \ln{ \left( \dfrac{3x - 6}{7x} \right)}\)

Exercice 10 : A partir de la courbe représentative de la fonction ln

Identifier les courbes de chacune des fonctions.

\begin{center}

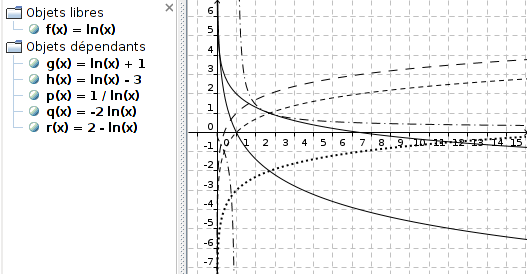
\end{center}

Exercice 11 : Variations sans calculer la dérivée

Soit les fonctions \(f\), \(g\) et \(h\) définies sur \(\mathbb{R}\) par :

\(f(x) = \ln(x) + \ln(2)\) , \(g(x) = \dfrac{\ln(x)}{5}\) et \(h(x) = 1-3\ln(x)\)

Déterminer le sens de variation de chacune de ces fonctions à partir de celui de la fonction \(\ln\).

Exercice 12 : Dérivées

Dans chacun des cas, justifier que \(f\) est dérivable sur \(\text{I}\) et déterminer sa dérivée.

\(f(x) = \dfrac{3x}{\ln(x)}\) sur \(\text{I} = \rbrack 1; + \infty \lbrack\)
\(f(x) = 3x^{2}\ln(x) - \ln (3)\) sur \(\text{I} = \mathbb{R}^{+*}\)
\(f(x) = \dfrac{\ln(x) + 1}{\ln(x) - 1}\) sur \(\text{I} = \rbrack e; + \infty \lbrack\)
\(f(x) = (\ln x)^2 - \dfrac{1}{\ln x}\) sur \(\text{I} = \rbrack 1; + \infty \lbrack\)

Exercice 13 : Tangente à la courbe

Déterminer les coordonnées du point de la représentation graphique \(\text{C}\) de la fonction ln en lequel la tangente \(\text{T}\) a pour coefficient directeur \(2\).

Exercice 14 : Signe d'une fonction grâce au sens de variation

Dans chaque cas, déterminer le signe de \(f(x)\) sur \(\mathbb{R}^{+*}\).

\(f(x) = 2x^2 - \ln x\)
\(f(x) = x\ln x + e\)

Exercice 15 : Déterminer une limite comportant une forme indéterminée

Déterminer les limites suivantes


1. \(\lim\limits_{x \to 0^+} x^2 - 3x\ln x\)	2. \(\lim\limits_{x \to +\infty} 4x^3 - 5x\ln x\)	3. \(\lim\limits_{x \to 0^+} \dfrac{\ln 2}{x} + \ln x\)
4. \(\lim\limits_{x \to 0} \dfrac{\ln(1 - x)}{2x}\)	5. \(\lim\limits_{x \to +\infty} (\ln x)^2 - 3\ln x + 2\)	6. \(\lim\limits_{x \to +\infty} \dfrac{\ln(e^x + 5)}{e^x}\)
7. \(\lim\limits_{x \to +\infty} 3x - e\ln x\)	8. \(\lim\limits_{x \to 0^+} 3x - e\ln x\)	9. \(\lim\limits_{x \to +\infty} \dfrac{\ln(1 + x) - 5x}{1 + x}\)
10. \(\lim\limits_{x \to -1^+} \dfrac{\ln(1 + x) - 5x}{1 + x}\)	11. \(\lim\limits_{x \to +\infty} \dfrac{\ln x}{\sqrt{x}}\)	12. \(\lim\limits_{x \to +\infty} \dfrac{e^x}{\ln x}\)

Exercice 16 : Déterminer une limite avec le nombre dérivé

Déterminer \(\lim\limits_{h \to 0} \dfrac{\ln(3 + h) - \ln 3}{h}\) et \(\lim\limits_{x \to 1} \dfrac{\ln(3x - 2)}{x - 1}\)

Exercice 17 : Inéquations comportant \(q^{n}\)

Les parties A et B sont indépendantes.

A. Déterminer le plus petit entier naturel \(n\) tel que :

\(3 \times \left( \dfrac{7}{9} \right)^n < 0,01\)
\(1 - 1,25^n < 0,99\)

B. On sait que le nombre d'atomes de carbone 14, en fonction du nombre \(n\) de siècles, est donné approximativement par \(q_{n} = q_{0}0,987976^{n}\), où \(q_0\) est le nombre initial d'atomes.

Déterminer la demi-vie du carbone 14 (durée au bout de laquelle la moitié des atomes de carbone 14 s'est désintégrée)
Déterminer l'âge des fragments trouvés par des archéologues, sachant que la teneur en carbone 14 est égale à 30 % de celle d'un fragment d'os actuel de la même masse pris comme témoin.

Exercice 18 : Avec des suites

Soit \(u\) la suite définie pour tout \(n \in \mathbb{N}^*\) par \(u_n = \ln \left( \dfrac{n}{n+1} \right)\).

Déterminer la limite de la suite \(u\).
\(\forall n \neq 0\), on note \(\text{S}_n = \sum\limits_{i = 1}^{n}u_i\)

a. Exprimer \(\text{S}_n\) en fonction de \(n\).

b. En déduire la limite de \(\text{S}_n\).

Fonctions du type \(x \mapsto \ln \left( u(x) \right)\)

Exercice 19 : Maîtriser le cours - Vrai ou faux

Soit \(u\) une fonction dérivable sur \(\mathbb{R}\) et à valeurs strictement positives.

\(\forall x \in \mathbb{R}\), \(\ln \left( u(x) \right) > 0\)
La fonction \(\ln(u)\) est dérivable sur \(\mathbb{R}\)
La dérivée de \(\ln(u)\) est \(\dfrac{1}{u}\) sur \(\mathbb{R}\)
\(\lim\limits_{x \to +\infty} \ln \left( u(x) \right) = +\infty\)
\(\ln \left( u(x) \right) \geqslant \ln 5 \Leftrightarrow x \geqslant 5\)
\(\ln \left( u(x) \right) \leqslant 5 \Leftrightarrow 0 < u(x) \leqslant e^5\)

Exercice 20 : Résoudre une équation ou une inéquation comportant \(\ln(u(x))\)

Résoudre les équations ou inéquations suivantes :

\(\ln(2x - 5) = \ln 4\)
\(\ln(2x - 5) = -3\)
\(\ln(7x + 2) \geqslant \ln(3 - x)\)
\(\ln \left(e^{2x} - 25 \right) \geqslant 0\)
\(\ln((x + 1)(x - 2)) \geqslant \ln {18}\)
\(\ln(1 - x^2) - \ln(x - 3) \geqslant 0\)

Exercice 21 : Signe d'une fonction

Étudier le signe des fonctions ci-dessous :

\(f(x) = (x-3)\ln(x - 1)\)
\(g(x) = \dfrac{\ln{x} - 1}{\ln(x - 1)}\)
\(h(x) = \ln \left( \dfrac{e^x - 3}{e^x - 1} \right)\)

Exercice 22 : Ensemble de définition

Déterminer dans chaque cas l'ensemble de définition de la fonction \(f\) :

\(f(x) = \ln (x^2) - 3\)
\(f(x) = \ln (e^x - 1)\)
\(f(x) = \ln (x^2 - 3)\)
\(f(x) = \dfrac{1}{\ln (x + 2)}\)
\(f(x) = \ln \left( 1 - \dfrac{1}{x^2} \right)\)

Exercice 23 : Tableau de variations

Donner le tableau de variations des fonctions ci-dessous :

\(f(x) = (\ln x)^2 - \ln(x^2)\) sur \(\text{I} = \mathbb{R}^{+*}\)
\(f(x) = (1 - x)\ln(1 - x)\) sur \(\text{I} = \rbrack -\infty;1 \lbrack\)
\(f(x) = \ln \left( \dfrac{e^x + 1}{2e^x + 3} \right)\) sur \(\text{I} = \mathbb{R}\)

Exercice 24 : Avec Xcas

\begin{center}

\end{center}

Soit \(f\) la fonction définie sur \(\mathbb{R}^+\) par \(f(x) = 2x^2 - (x^2 + 1)\ln(x^2+1)\)

Répondre aux questions ci-dessous, en utilisant les résultats ci-dessus fourni par le logiciel de calcul formel Xcas.

Étudier le sens de variation de \(f\) sur \(\mathbb{R}^+\).
Montrer que dans l'intervalle \(\left\lbrack \sqrt{e - 1};\sqrt{e^{2} - 1} \right\rbrack\), l'équation \(f(x) = 0\) admet une solution unique \(\alpha\).

Donner une valeur approchée de \(\alpha\) à \(10^{-2}\).
En déduire le signe de \(f(x)\) sur \(\mathbb{R}^+\).

La fonction logarithme décimal

La fonction logarithme népérien est particulièrement intéressante du fait de sa propriété de transformation d'un produit en somme. Mais comme on utilise, pour écrire les nombres, le système décimal, on lui préfère parfois une autre fonction possédant la même propriété de transformation de produit en somme mais prenant la valeur 1 lorsque \(x = 10\) (et donc la valeur 2 lorsque \(x = 100\), la valeur 3 lorsque \(x = 1000\) etc...)

Cette fonction sera appelée fonction logarithme décimal ou fonction logarithme de base 10.

Définition :

On appelle fonction logarithme décimal et on note \(\log\) la fonction définie sur \(\rbrack{0; + \infty}\lbrack\) par :

\[\log : \rbrack 0; + \infty \lbrack \to \mathbb{R} \quad \quad \quad\]

\[\quad \quad \quad x \mapsto\dfrac{\ln x}{\ln {10}}\]

La fonction logarithme décimal étant définie par \(\log x = k \times \ln x\) avec \(k = \dfrac{1}{\ln 10}\) , il est facile d'étudier ses variations et de donner sa courbe représentative. les formules sont identiques à celles de la fonction logarithme népérien :

\(\log 1 = 0\), \(\log {10} = 1\),

\(\log(a \times b) = \log a + \log b\),

\(\log\dfrac{1}{a} = - \log a\),

\(\log\dfrac{a}{b} = \log a - \log b\),

\(\log\sqrt{a} = \dfrac{1}{2}\log a\) et \(\log a^{n} = n\log a\)

Exercice 25 : Vrai ou faux

\(\log(e) = 1\)
\(\log(10^{-5}) = -5\)
\(\log(10^2 \times 10^3) = 5\)
\(\log(x) < 1 \Leftrightarrow 0 < x < 10\)
\(\log(x) = - 3\log(5) \Leftrightarrow x = \dfrac{1}{125}\)
\(\left(\log(x)\right)' = \log (e) \ln(x)\)

Exercice 26 : Niveau sonore

Le niveau sonore \(\text{N}\) d'un bruit, exprimé en décibels (dB), est donné par \(\text{N} = 10\log \left( \dfrac{\text{I}}{\text{I}_0} \right)\), où \(\text{I}\) est l'intensité sonore exprimé en W/\(m^{2}\), et où \(\text{I}_0\) est l'intensité de référence correspondant à la plus petite intensité acoustique audible.

On sait que, lorsqu'on met en présence plusieurs sources sonores, les intensités s'additionnent.

Le niveau sonore d'un lave-linge est de 50 dB. Quel est le niveau sonore de deux lave-linge identiques ? Le niveau sonore a-t-il doublé ?
Le niveau sonore d'une note de musique obtenue au violon est de 70 dB. Combien faut-il de violonistes jouant ensemble la même note, pour obtenir un niveau sonore de 80 dB ?
Le niveau sonore d'un marteau-piqueur est de 110 dB et celui d'un klaxon de voiture est de 80 dB. Quel est le niveau sonore des deux bruits réunis ? Que remarque-t-on ?

Exercice 27 : Algorithme de Briggs

Dans introduction à l'analyse infinitésimale (1748), Euler explique la méthode de Briggs pour calculer une valeur approchée de \(\log(5)\). Ses calculs sont donnés dans le tableau ci-dessous :


Les calculs sont initialisés par		La méthode de Briggs
\(\text{A} = 1\)		utilise la relation
\(\text{B} = 10\)		\(\log(\sqrt{AB}) =\dfrac{1}{2} \left( \log {\text{A}}+\log {\text{B}} \right)\)
\({\ell_A} = 0\)		\(C=\sqrt{\text{AB}}\)
\({\ell_B} = 1\)		et \({\ell_C} = \dfrac{1}{2} (\ell_A + \ell_B)\)

Pour la suite des calculs, on procède de la façon suivante et on considère uniquement les variables \(A\) et \(B\):

si \(\sqrt{\text{AB}} \leqslant 5\), alors :

A prend la valeur \(\sqrt{\text{AB}}\) et \({\ell_A}\) prend la valeur \(\dfrac{\ell_A + \ell_B}{2}\)
si \(\sqrt{\text{AB}} > 5\), alors :

B prend la valeur \(\sqrt{\text{AB}}\) et \({\ell_B}\) prend la valeur \(\dfrac{\ell_A + \ell_B}{2}\)

Ce qui donne :

\(A = 3.1622776601683795\) \(\ell_A = 0.5\)

\(B = 5.623413251903491\) \(\ell_B = 0.75\)

\(A = 4.216965034285822\) \(\ell_A = 0.625\)

\(A = 4.869675251658631\) \(\ell_A = 0.6875\)

\(B = 5.232991146814947\) \(\ell_B = 0.71875\)

\(B = 5.0480657166674705\) \(\ell_B = 0.703125\)

\(A = 4.958068241684655\) \(\ell_A = 0.6953125\)

\(B = 5.002864610575233\) \(\ell_B = 0.69921875\)

\(A = 4.980416061248411\) \(\ell_A = 0.697265625\)

\(A = 4.991627716362686\) \(\ell_A = 0.6982421875\)

\(A = 4.99724300503361\) \(\ell_A = 0.69873046875\)

\(B = 5.00005301775164\) \(\ell_B = 0.698974609375\)

\newpage

Vérifier les 4 premières lignes de calcul.

Compléter l'algorithme suivant écrit en Python, afin qu'il applique l'algorithme de Briggs pour le calcul de \(\log{(x)}\) où \(x\) est un réel compris entre \(10\) et \(100\) avec une précision de \(10^{-k}\).

On initialisera l'algorithme avec :

A=10, B=100, lA=1 et lB=2

from math import *
def CalculeLog_x( x, k ):
    A = .........
    B = .........
    lA = .........
    lB = .........
    precision = 10**(.........)
    while (B - x > ............ ):
        if (sqrt(A * B)< ......):
            ...... = sqrt(A*B)
            ...... = 1/2*(lA + lB)
        else:
            ...... = sqrt(A*B)
            ...... = 1/2*(lA + lB)
    return lB

En déduire une valeur approchée à \(10^{-10}\) près de \(\log(85)\)

Vu au baccalauréat

Exercice 28 :

Dans tout le problème, \(n\) désigne un entier naturel non nul.

Soit \(g_n\) la fonction définie sur \(]0 ; +\infty [\) par \(g_n(x) = x−n +\dfrac{n}{2}\ln{x}\).

Étudier les variations de \(g_n\)

Déterminer les limites de \(g_n\) en \(0\) et en \(+\infty\).
a. En déduire l'existence d'un réel positif αn unique tel que \(g_n(\alpha_n) = 0\).

b. Montrer que : \(1 \leqslant \alpha_n < e^2\).

c. Montrer que : \(\ln(\alpha_n) = 2−\dfrac{2}{n}\alpha_n\)

Exprimer \(g_{n+1}(\alpha_n)\) en fonction de \(\alpha_n\) et de \(n\).

En déduire que \(\alpha_{n+1} > \alpha_n\).
a. Montrer que la suite de terme général \(\alpha_n\) est convergente. On note \(\ell\) sa limite.

b. En utilisant 2.c., calculer \(\lim\limits_{n \to +\infty}\ln(\alpha_n)\) et en déduire \(\ell\).

Exercice 29 : Pondichéry 2004

Soit \(u\) la suite définie par : \(\left\{\begin{array}{l c l} u_0 &=&0\\ u_{n+1} &=& \dfrac{1}{2 - u_n}\quad \text{pour tout entier naturel}~n\\ \end{array} \right.\)

a. Calculer \(u_1\),\(u_2\) et \(u_3\). On exprimera chacun de ces termes sous forme d'une fraction irréductible.

b. Comparer les quatre premiers termes de la suite \(u\) aux quatre premiers termes de la suite \(w\) définie sur \(\mathbb{N}\) par \(w_n = \dfrac{n}{n+1}\).

c. À l'aide d'un raisonnement par récurrence, démontrer que, pour tout entier naturel \(n,\:u_n = w_n\).
Soit \(v\) la suite de terme général \(v_n\) défini par \(v_n = \ln \left(\dfrac{n}{n+1}\right)\) où \(\ln\) désigne la fonction logarithme népérien.

a. Montrer que \(v_1 + v_2 + v_3 = - \ln 4\).

b. Soit \(S_n\) la somme définie pour tout entier naturel non nul \(n\) par :

\[ S_n = v_1 + v_2 + \cdots + v_n. \]

Exprimer \(S_n\) en fonction de \(n\).

Déterminer la limite de \(S_n\) lorsque \(n\) tend vers \(+\infty\).