Feuille d'exercices sur la continuité

Continuité : maîtriser le cours

Exercice 1 : Vrai ou faux

Soit \(f\) une fonction définie sur un intervalle \(I\) et \(\text{C}\) sa courbe représentative dans un repère \((\text{O};\overrightarrow{\imath},\overrightarrow{\jmath})\).

Si \(f\) est continue sur \(\text{I}\), alors :

On peut tracer une tangente non verticale en tout point de \(\text{C}\).
\(f\) est une fonction qui ne change pas de sens de variation.
\(\text{C}\) se trace sans lever le crayon.
L'intervalle \(\text{I}\) est fermé.
La fonction inverse est continue sur \(\rbrack -\infty;0 \lbrack\)
La fonction valeur absolue est continue sur \(\mathbb{R}\).
La fonction racine carrée est continue sur \(\mathbb{R}^+\).

Justifier la continuité d'une fonction sur un intervalle

Exercice 2

Montrer que les fonctions suivantes sont continues sur l'intervalle \(I\) indiqué.

\(f:x \mapsto \sqrt{3 - x}\) sur \(\text{I} = \rbrack - \infty;3 \lbrack\)
\(f:x \mapsto 2 \left| x \right| + \dfrac{3}{x}\) sur \(\rbrack 0; +\infty \lbrack\)
\(f:x \mapsto \dfrac{3x^3}{1 - 3x}\) sur \(\text{I} = \left\rbrack \dfrac{1}{3}; +\infty \right\lbrack\)
\(f:x \mapsto \left| 2x - 3 \right|\) sur \(\text{I} = \mathbb{R}\)

Continuité et représentation graphique

Exercice 3

Déterminer graphiquement si les fonctions dont les courbes représentatives sont données ci-dessous sont continues sur l'intervalle \(\lbrack -4;6 \rbrack\).
```
\begin{center}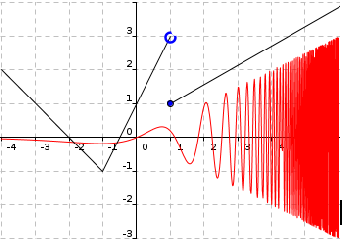
```
```
\end{center}
```
Représenter avec un traceur de courbes la fonction \(f:x \mapsto \dfrac{\sin\left(\frac{1}{x}\right)}{x}\).

\(f\) est-elle continue sur \(\rbrack 0;1 \rbrack\) ?

Essayer de tracer \(f\) à la main sans lever le crayon. Que peut-on conclure ?

\newpage

Exercice 4

On a tracé ci-dessous la courbe représentative d'une fonction \(f\) définie sur \(\lbrack -2;4 \rbrack\).

\begin{center}

\end{center}

La fonction \(f\) est-elle dérivable en \(-1,5\), en \(0\), en \(2\) ?
La fonction \(f\) est-elle continue sur \(\lbrack - 2;2 \rbrack\), sur \(\lbrack -2;-1 \rbrack\), sur \(\lbrack -2;-1 \lbrack\) ?
Déterminer \(\lim\limits_{x \to 2^+}f(x)\), \(\lim\limits_{x \to 2^-}f(x)\) . la fonction \(f\) est-elle continue en \(2\) ?

Exercice 5: Avec GeoGebra

Soit \(a\) un entier et \(f_a\) la fonction définie sur \(\mathbb{R}\) par :

\[\left\{ \begin{matrix} f_{a}(x) = x^2 - ax + 3 \; \text{si}\; x < 2 \\ f_{a}(x) = - x^2 + 8x + 3 \;\text{si} \; x \geq 2 \end{matrix} \right.\]

Conjecturer avec GeoGebra, l'entier \(a\) tel que la fonction \(f_a\) soit continue sur \(\mathbb{R}\).
Démontrer la conjecture précédente.

Avec la fonction partie entière

On note \(E\) la fonction partie entière.

Exercice 6

Soit la fonction \(f\) définie sur \(\mathbb{R} - \left\{ -1 \right\}\) par \(f(x) = \text{E}\left(\frac{x}{x + 1}\right)\).

Tracer la courbe représentative de \(f\) avec l'outil de votre choix. Que peut-on conjecturer sur \(\mathbb{R}^+\) ?
Démontrer la conjecture précédente.
Que peut-on en déduire au sujet de la continuité de la fonction \(f\) sur \(\mathbb{R}^+\) ?

Exercice 7

Soit les fonctions \(f\) et \(g\) définies sur \(\lbrack -5;5 \rbrack\) par \(f(x) = x \left| x \right|\) et \(g(x) = (2x + 1)\left| x \right|\).

Tracer les courbes représentatives de \(f\) et de \(g\) avec l'outil de votre choix.
\(f\) et \(g\) sont-elles continues ?
Que peut-on conjecturer graphiquement au sujet de la dérivabilité en \(0\) de \(f\) et de \(g\) ?
Démontrer les deux conjectures précédentes.
La fonction valeur absolue est-elle dérivable en 0 ? Peut-on énoncer une règle concernant la dérivabilité du produit d'une fonction dérivable par une fonction non dérivable ?

\newpage

Image d'une suite convergente par une fonction continue

Exercice 8 : limite de \(f(u_n)\)

Soit \((v_n)\) la suite définie pour tout entier naturel \(n \geqslant 2\) par :

\[v_n = \text{e}^{\frac{n-1}{n+1}}\]

Proposer une suite \((u_n)\) et une fonction \(f\) telles que pour tout entier naturel \(n \geqslant 2\), \(v_n=f(u_n)\)
Déterminer la limite de \((v_n)\).

Exercice 9 : limite de \(f(u_n)\)

Soit \((v_n)\) la suite définie pour tout entier naturel par :

\[v_n = \sin \left( \frac{\pi n^2-3}{n^2+3}\right)\]

Proposer une suite \((u_n)\) et une fonction \(f\) telles que pour tout entier naturel , \(v_n = f(u_n)\)
Déterminer la limite de \((v_n)\).

Exercice 10 : \(u_{n+1} = f(u_n)\)

Soit \((u_n)\) la suite définie par : \(\left\{ \begin{matrix} u_{0} = 1 \\ u_{n+1} = u_n\text{e}^{- u_n} \end{matrix} \right.\)

Démontrer que pour tout entier naturel \(n\), on a :

\[0 \leqslant u_{n+1} \leqslant u_n \leqslant 1\]
En déduire que la suite \((u_n)\) converge vers un réel \(L\), puis déterminer \(L\).

Exercice 11 : \(u_{n+1} = f(u_n)\)

Soit \((u_n)\) la suite définie par :

\[\left\{ \begin{matrix} u_{0} = 1 \\ u_{n+1} = \dfrac{u_n}{1+{u_n}^2} \end{matrix} \right.\]

Démontrer que pour tout entier naturel \(n\), on a :

\[0 \leqslant u_{n+1} \leqslant u_n \leqslant 1\]
En déduire que la suite \((u_n)\) converge vers un réel \(L\), puis déterminer \(L\).

Théorème des valeurs intermédiaires - Théorème des bijections

Exercice 12 : Maîtriser le cours - Vrai ou faux

Soit \(f\) une fonction définie sur un intervalle \(I\).

Si \(f\) change de signe sur \(I\), alors \(f\) s'annule sur \(I\).
Si \(\text{I} = \lbrack a;b \rbrack\), \(f(a)f(b) > 0\) et \(f\) est continue sur \(I\), alors \(f\) s'annule sur \(I\).
Si \(f\) s'annule une unique fois sur \(I\) et \(f\) est strictement monotone sur \(I\), alors \(f\) est continue sur \(I\).
Si \(f\) s'annule une unique fois sur \(I\) et \(f\) est continue sur \(I\), alors \(f\) est strictement monotone sur \(I\).

Exercice 13 : Au moins une solution

Montrer que l'équation \((\text{E}):\dfrac{x^3}{x + 1} = 8\) admet au moins une solution sur \(\text{I} = \lbrack 0;4 \rbrack\).

Exercice 14 : Une unique solution - utiliser Solve() et nSolve()

Dans chacun des cas, montrer que l'équation admet une unique solution \(\alpha\) sur l'intervalle \(I\) et donner un encadrement de \(\alpha\) d'amplitude \(10^{-2}\) en utilisant les fonctions de la calculatrice :

Solve() : fonction de calcul formel .

Elle cherche à appliquer divers algorithmes permettant de résoudre certains types d'équations prédéfinis (équations linéaires, du 2nd, du 3ème ou du 4ème degré, équation avec des racines carrées se ramenant aux types précédents, équations avec des 'cos' et 'sin', etc.)

nSolve() : fonction fournissant une valeur approchée par la méthode de Newton-Raphson. Par nature, cette fonction ne peut retourner qu'une seule solution même s'il en existe plusieurs. Elle peut aussi ne rien retourner du tout (plus exactement, elle retourne 'false'), voire retourner un résultat erroné dans les (rares) cas où la méthode de Newton ne converge pas. Suivant l'outil utilisé (Xcas, Mathematica, Ti-Nspire ... ) , il est possible de préciser l'intervalle sur lequel la solution est cherchée ou la valeur initiale pour appliquer le méthode de Newton-Raphson.
\((\text{E}) : \sqrt{1 - x} = x\) sur \(\text{I} = \rbrack -\infty;1 \lbrack\)
\((\text{E}) : 5x\text{e}^{-x} = 1\) sur \(\text{I} = \lbrack 1;+\infty \lbrack\)

Exercice 15 : Signe de f(x)

Soit \(f\) une fonction définie et continue sur \(\mathbb{R}\) telle que :

Les solutions de l'équation \(f(x) = 0\) sont \(-4\) et \(3\).
Les solutions de l'équation \(f(x) = {-2}\) sont \(-9\) et \(4\).
\(f(0) = 2\)

Déterminer le signe de \(f(x)\) suivant les valeurs de \(x\).

Exercice 16 : Signe de f(x)

On donne le tableau de variation d'une fonction \(f\).

\begin{center}

\end{center}

Combien l'équation \(f(x) = 0\) admet-elle de solutions sur \(\rbrack - \infty;0 \lbrack\)?
Combien l'équation \(f(x) = 0\) admet-elle de solutions sur \(\rbrack 0;+\infty \lbrack\)?
En déduire le signe de \(f(x)\) suivant les valeurs de \(x\).

Exercice 17 : Signe de f(x)

On donne le tableau de variation d'une fonction \(f\).

\begin{center}

\end{center}

Combien l'équation \(f(x) = 0\) admet-elle de solutions sur \(\rbrack -\infty;3 \lbrack\)?

À quel intervalle appartient chacune d'elle ?
Combien l'équation \(f(x) = 0\) admet-elle de solutions sur \(\rbrack 3;+\infty \lbrack\) ?
En déduire le signe de \(f(x)\) suivant les valeurs de \(x\).

\newpage

Exercice 18 : \(f(x) = k\) : discussion suivant les valeurs de \(k\)

On donne le tableau de variation d'une fonction \(f\) définie et dérivable sur \(\mathbb{R}\).

\begin{center}

\end{center}

Déterminer les extrema de \(f\).
Combien l'équation \(f(x) = 0\) admet-elle de solutions sur \(\mathbb{R}\) ?
Déterminer le signe de \(f\).
Discuter suivant les valeurs du réel \(k\), le nombre de solutions de l'équation \(f(x) = k\).

Exercice 19 : Tableau de variation de \(f\) à partir du tableau de variation de \(f'\)

Soit \(f\) une fonction définie et dérivable sur \(\mathbb{R}\), dont la fonction dérivée \(f'\) (\(f'\) étant continue) admet le tableau de variation suivant:

\begin{center}

\end{center}

Déterminer le signe de \(f'(x)\) suivant les valeurs de \(x\) et en déduire les variations de \(f\).

Exercice 20 : Existence d'au moins une solution

Soit \(f\) une fonction définie et continue sur \(\text{I} = \lbrack 0;1 \rbrack\) , telle que pour tout \(x \in \text{I}\), \(f(x) \in \text{I}\).

Montrer qu'il existe au moins un réel \(\alpha \in \text{I}\), tel que \(f(\alpha) = \alpha\).

Exercice 21 : Discuter suivant les valeurs de \(n\)

Soit \(n \in \mathbb{N}^*\) et \(a \in \mathbb{R}\).

Discuter suivant les valeurs de \(n\) et de \(a\), le nombre de solutions de l'équation \(x^n = a\).

\newpage

Algorithme - Python

Exercice 22 : Méthode de la sécante

Introduction :

Dans un repère orthonormé \((\text{O};\overrightarrow{\imath},\overrightarrow{\jmath})\), on considère la fonction \(f\) définie par \(f(x) = x^3 + x - 3\) et sa courbe représentative \(\text{C}_{f}\) représentée ci-dessous.
```
\begin{center}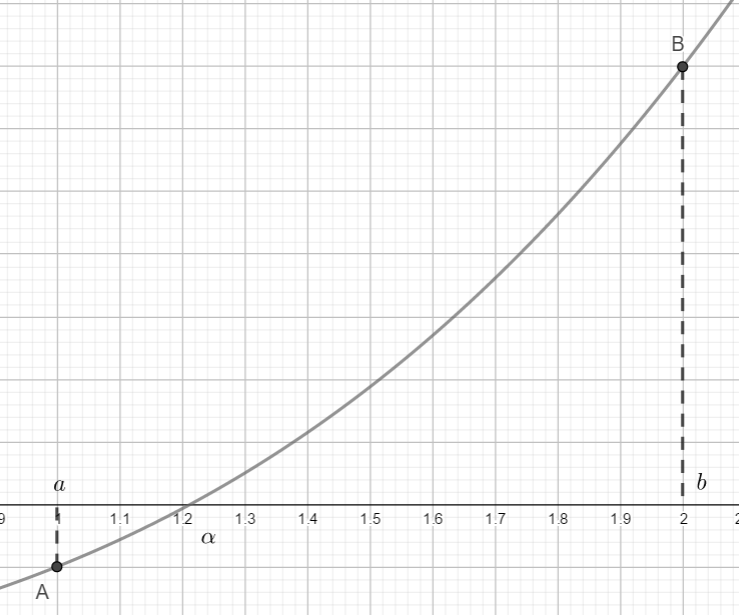
```
```
\end{center}
```
On montre facilement grâce au corollaire du théorème des valeurs intermédiaires que l'équation \(f(x) = 0\) admet une unique solution \(\alpha\) dont nous allons déterminer une valeur approchée par la méthode de la sécante.

On considère les points \(\text{A}(1;f(1))\) et \(\text{B}(2;f(2))\)

Étape 1 :

Tracer le segment \(\lbrack \text{AB} \rbrack\) : il coupe l'axe des abscisses en un point d'abscisse \(x_1\), puis placer le point \(\text{A}_1(x_1;f(x_1))\).

Étape 2 :

Tracer le segment \(\left\lbrack {\text{A}_{1}\text{B}} \right\rbrack\) : il coupe l'axe des abscisses en un point d'abscisse \(x_{2}\), puis placer le point \(\text{A}_2(x_2;f(x_2))\).

Et ainsi de suite ...

En notant \(x_n\) l'abscisse du point \(\text{A}_n\), on définit ainsi une suite \((x_n)\) de réels de \(\lbrack a;b \rbrack\) et on admet (grâce à la convexité) que pour tout entier naturel \(n\), \(f(x_n) \leqslant 0\).
Mise en place de l'algorithme :

Revenons sur le cas général.

Soit \(f\) une fonction strictement croissante, continue et convexe sur un intervalle \(\lbrack a;b \rbrack\) telle que \(f(a) < 0\) et \(f(b) > 0\).

On considère les points \(\text{A}(a;f(a))\) et \(\text{B}(b;f(b))\)

On note \(\text{C}_f\) sa courbe représentative.

a. Déterminer une équation de la droite \((\text{A}_n\text{B})\)

b. En déduire que \(x_{n+1} = x_n - \dfrac{b - x_n}{f(b) - f(x_n)}f(x_n)\)

c. Démontrer que la suite \((x_n)\) est croissante et majorée.

d. En déduire que \((x_n)\) est convergente, puis déterminer sa limite.

On s'intéresse à nouveau à la fonction \(f\) définie par \(f(x) = x^3 + x - 3\).

Compléter les pointillés dans le programme suivant écrit en Python pour qu'il affiche les valeurs la suite \((x_n)\) jusqu'à \(n = 20\).

N=int(input("N="))
a=float(input("a="))
b=float(input("b="))
def f(x):
  return (............)

def Methodesecante(a,b, N):
  x=............
  for i in range(............):
    x.append(................................................)
  return x

print(Methodesecante(............))

Tester ce programme et comparer avec la méthode de Newton. (chapitre suite : Exercice 25 )

On se propose maintenant pour éviter les calculs inutiles de stopper le programme quand la différence entre deux termes consécutifs de la suite est inférieure à une précision \(p\).

Pour cela, compléter les pointillés dans le programme ci-dessous :

from math import *
p=float(input("p="))
a=float(input("a="))
b=float(input("b="))

def f(x):
  return (........................)

def Methodesecante(a,b,p):
  x=............
  i=............
  x.append(................................................)
  while (........................):
    i=i+1
    x.append(................................................)
  return x

print(Methodesecante(........................))