Devoir de Mathématiques sur les nombres complexes.
L'usage de la calculatrice n'est pas autorisé.
Durée : 1h15
Exercice 1
Résoudre dans \(\mathbb{C}\) l'équation:
Corrigé
\(1\) est racine évidente car la somme des coefficients vaut \(0\).
d'où \(z^3+3z^2+z-5=(z-1)(z^2+4z+5)\) en divisant \(z^3+3z^2+z-5\) par \((z-1)\)
On obtient un trinôme du second degré, calculons son discriminant \(\Delta\).
\(\Delta=16-4 \times 5=-4\)
On a donc deux racines complexes pour le trinôme du second degré:
\(z_1=-2-i\) et \(z_2=-2+i\)
L'ensemble \(S\) des solutions de l'équation du départ est donc:
Exercice 2
Construction d'un pentagone régulier à la règle et au compas.
Le plan complexe est muni d'un repère orthonormé direct \((O ; \vec{u},\vec{v})\).
On pose: \(a = e^{i\frac{2\pi}{5}}\)
-
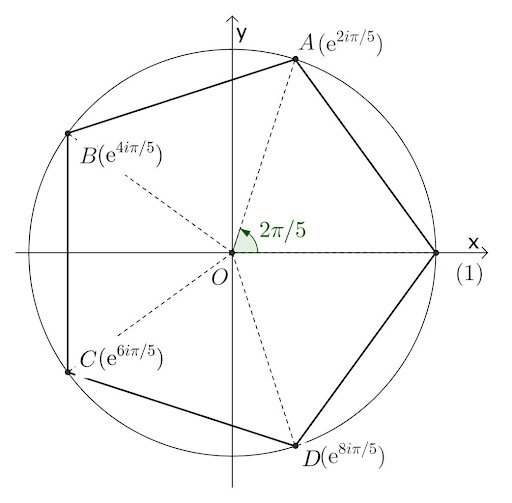
Soit I, A, B, C, D les points du plan complexe d'affixes respectives 1, \(a\), \(a^2\), \(a^3\), \(a^4\).
a. Vérifier que \(a^5 = 1\).
b. Faire une figure. On prendra 4 cm pour unité graphique.
c. Vérifier que les points I, A, B, C, D sont les sommets d'un pentagone régulier inscrit dans le cercle \(C\) de centre O et de rayon 1.
-
a. Vérifier que : \(\forall z \in \mathbb{C}\), \(z^5-1 = (z-1)(1+z+z^2+z^3+z^4)\).
En déduire que: \(1 + a + a^2 + a^3 + a^4 = 0\).
b. Démontrer que : \(a^3 = {\overline{a}}^2\) et \(a^4 = \overline{a}\).
En déduire que: \((a + \overline{a})^2 + (a+\overline{a})-1= 0\) (R).
c. Résoudre dans \(\mathbb{R}\) l'équation \(x^2+x-1 = 0\).
En déduire, en utilisant la relation (R), la valeur exacte de \(\cos\left(\dfrac{2\pi}{5}\right)\)
-
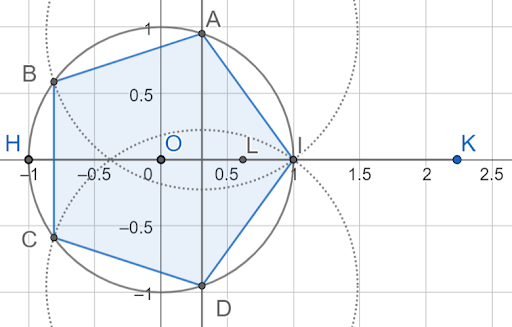
Sur une nouvelle figure
a. Construire à la règle et au compas un segment de longueur \(\sqrt{5}\).
b. Construire à la règle et au compas un cercle de centre O et de rayon 1, deux axes gradués perpendiculaires d'origine O, le point H d'abscisse -1 dans ce repère, le point K d'abscisse \(\sqrt{5}\), le milieu L du segment [HK], puis le milieu F du segment [OL].
c. En déduire une construction à la règle et au compas d'un pentagone régulier.
Corrigé
1.a. \(a=e^{i \frac{2 \pi}{5}}\) donc \(a^5=\left( e^{i \frac{2 \pi}{5}} \right)^5 = e^{2 i \pi} = 1\)
c. \(\left|{a}\right|= 1\) donc les points I, A, B, C et D sont bien sur le cercle trigonométrique.
De plus, tous les angles au centre valent \(\dfrac{2 \pi}{5}\) donc les points sont bien sur un pentagone régulier inscrit dans le cercle trigonométrique.
2.a. Évident en développant.
Ainsi, \(a^5-1 = (a-1)(1+a+a^2+a^3+a^4)\)
Sachant que \(a^5 -1 = 0\) et que \(a \neq 1\) (donc \(a-1 \neq 0\)), on en déduit que \(1 + a + a^2 + a^3 + a^4=0\).
2.b. \(a^3=\left( e^{i \frac{2 \pi}{5}} \right)^3 = e^{i \frac{6 \pi}{5}} = e^{i \frac{-4 \pi}{5}}= \left(e^{-i \frac{2 \pi}{5}}\right)^2 = \bar{a}^2\)
De même, \(a^4=\left( e^{i \frac{2 \pi}{5}} \right)^4 = e^{i \frac{8 \pi}{5}} = e^{i \frac{-2 \pi}{5}}= \bar{a}\)
\((a+ \bar{a})^2 + (a+ \bar{a}) - 1 = a^2 + 2 a \bar{a} + \bar{a}^2 + a + \bar{a} - 1 = a^2 + 2 + a^3 + a + a^4 - 1 = 1 + a + a^2 + a^3 + a^4 = 0\)
2.c. En utilisant le discriminant, on trouve que cette équation a deux solutions : \(x_1 = (-1+\sqrt{5})/2\) et \(x_2 = (-1-\sqrt{5})/2\)
D'apres la question précédente, on a donc \(a + \bar{a} = x_1\) ou \(a + \bar{a} = x_2\).
Or, \(a + \bar{a} = 2 Re(a) = 2 cos \left(\frac{2 \pi}{5} \right)\). Ainsi on en déduit que \(cos \left(\frac{2 \pi}{5} \right) = \frac{-1+\sqrt{5}}{4}\) ou \(cos \left(\frac{2 \pi}{5} \right) = \frac{-1-\sqrt{5}}{4}\).
Mais on sait que \(cos \left(\frac{2 \pi}{5} \right) > 0\) donc on trouve que \(cos \left(\frac{2 \pi}{5} \right) = \frac{-1+\sqrt{5}}{4}\)
3.a. Il suffit de faire la diagonale d'un rectangle de longueur 2 et de largeur 1 (et se souvenir de Pythagore).
3.b. 
3.c. On trace la bissectrice de [OL], elle coupe le cercle en A et D. Ensuite, on reporte la distance AI sur le cercle pour placer B et C.
Exercice 3
Soit (E) l'équation
Sachant que (E) admet des solutions réelles, résoudre cette équation.
Corrigé
Soit \(a \in \mathbb{R}\) une solution de (E).
\(a^4−3a^3+(2−i)a^2+3a−3+i=0 \Rightarrow a^4−3a^3+2a^2+3a−3+i(−a^2+1)=0\)
\(a^4−3a^3+(2−i)a^2+3a−3+i=0 \Rightarrow a^4−3a^3+2a^2+3a−3=0\) et \(a^2-1=0\)
\(-1\) et \(1\) sont solutions de \(a^2-1=0\), et aussi solutions de l'équation \(a^4−3a^3+2a^2+3a−3=0\)
\(X^4-3X^3+(2-i)X^2+3X-3+i\) peut donc être factorisé sous la forme \((X^2-1)(X^2-3X+3-i)\).
Le trinôme du second degré à coefficients complexes \(X^2-3X+3-i\) a pour discriminant \(\Delta=9-4(3-i)=-3+4i\)
On cherche donc \(\delta=a+ib\) tel que \((a+ib)^2=-3+4i\).
Soit \(a^2-b^2=-3\) et \(2ab=4\) soit \(ab=2\).
avec \(b=\dfrac{2}{a}\) on trouve \(a\) solution de \(a^2-\dfrac{4}{a^2}=-3\)
En posant \(A=a^2\), on a \(A^2+3A-4=0\) Soit \(A=1\) ou \(A=-4\).
Comme \(a\) est un nombre réel, on a \(a=-1\) ou \(a=1\) donc \(\delta=1+2i\) ou \(\delta=-1-2i\).
L'ensemble \(S\) des solutions de l'équation du départ est donc: