Aller au contenu

Feuille d'exercices sur les nombres complexes : Partie Géométrique

Affixes de points et de vecteurs

On se place dans un repère orthonormé \((\text O;\overrightarrow{u},\overrightarrow{v})\) .

Exercice 1 : Calculs d'affixes

  1. Déterminer les affixes des points suivants : \(\text A(2;0)\)  , \(\text B(0;-5)\)   et \(\text C(-2;3)\).

  2. Déterminer les affixes des vecteurs suivants : \(-3\overrightarrow{u}\) ;  \(5\overrightarrow{u}\) ;   \(3\overrightarrow{u}-5\overrightarrow{ {v}}\).

  3. Déterminer les affixes des vecteurs \(\overrightarrow{ {\text{AB}}}\) et \(\overrightarrow{ {\text{CD}}}\) : \(\text A(2;5)\) , \(\text B(1;3)\) , \(\text C(3;0)\) et \(\text D(-3;2)\)

Exercice 2 : Vecteurs colinéaires

  1. Soit \(\overrightarrow{t}\)  d'affixe \(3-i\)  , \(\text A(3 ,-1)\)  et \(\text B(x ,3)\) .

    Pour quelle valeur de \(x\) , \(\overrightarrow{ {t}}\) est-il colinéaire à \(\overrightarrow{ {\text{AB}}}\) ?

  2. Soit \(\text A(3;4)\) , \(\text B(1 ,2)\)  ,\(\text C(a;0)\)  et \(\text D(4;-b)\) .

    Pour quelles valeurs de \(a\)  et \(b\) , \(\text{ABCD}\) est-il un parallélogramme ?

Exercice 3 : Lire et calculer des affixes

  1. Lire les affixes des points A, B et C.

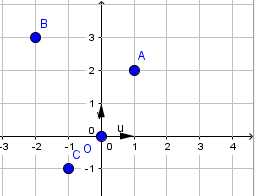
    Repère

  2. Lire les affixes des vecteurs \(\overrightarrow{ {\text{AB}}}\) , \(\overrightarrow{ {\text{AC}}}\)  et \(\overrightarrow{ {\text{CB}}}\) .

  3. Déterminer les affixes des milieux des côtés du triangle ABC.

Exercice 4 : Affixe et parallélogramme

Soit A, B et C les points d'affixes \(z_{\text A}=5-i\) , \(z_{\text B}=4-3i\)  et \(z_{\text C}=-2+2i\) .

  1. Déterminer l'affixe du vecteur \(\overrightarrow{ {\text{AB}}}\) .

  2. Déterminer l'affixe de D tel que ABCD soit un parallélogramme.

  3. Vérifier que ses diagonales ont le même milieu.

Exercice 5 : Affixes de vecteurs et droites

Soit A, B, C et D les points d'affixes \(z_{\text A}=4+i\) , \(z_{\text B}=3-2i\) , \(z_{\text C}=1+3i\)  et \(\text z_{\text D}=-1+9i\) .

Déterminer les affixes des vecteurs \(\overrightarrow{ {\text{AB}}}\)  et \(\overrightarrow{ {\text{DC}}}\) .

Que peut-on dire des droites \((\text{AB})\)  et \((\text{CD})\) ?

Exercice 6 : Affixes, centre de gravité et points alignés

Soit A, B et C les points d'affixes \(z_{\text A}=3+2i\)  , \(z_{\text B}=4-3i\)  et \(z_{\text C}=-2+2i\) . ) Déterminer l'affixe du centre de gravité G de ABC. (Le centre de gravité G vérifie \(\overrightarrow{ {\text{GA}}}\) + \(\overrightarrow{ {\text{GB}}}\) + \(\overrightarrow{ {\text{GC}}}\) = \(\overrightarrow{ {0}}\) ) ) Déterminer l'affixe du milieu I de \(\text{[BC]}\) et montrer que les points A,I et G sont alignés.

Exercice 7 : Ensembles de points

Dans le plan complexe muni d'un repère orthonormé \((\text O;\overrightarrow{u} ,\overrightarrow{ {v}})\) , déterminer dans chacun des cas l'ensemble des points M d'affixe \(z=x+\mathit{iy}\)  

  1. \(3z+5i\overline z=7-2i\)

  2. \((1-2i)z+(1+2i)\) \(\overline z\) = \(z\overline z\)

  3. \(z^2+\overline z\in \mathbb{R}\)

  4. \((1+ z )(i+\overline z) \in i\mathbb{R}\)

  5. \(\dfrac{z+1-2i}{z-3+2i}\in \mathbb{R}\)

  6. \(\dfrac{z+1-2i}{z-3+2i}\in i\mathbb{R}\)

Forme trigonométrique - module et arguments

Exercice 8

  1. Soit \(z\)  un nombre complexe de module \(r\)  et d'argument \(\theta\) . Déterminer \(\left|-z\right|\) , \(\left|\mathit{iz}\right|\)  , \(\text{arg}\left(-z\right)\)  et \(\text{arg}\left(\mathit{iz}\right)\)

  2. Déterminer les longueurs AB et CD avec \(z_{\text A}=2+3i\) , \(z_{\text B}=1+4i\) , \(z_{\text C}=3i\)  et \(z_{\text D}=5-2i\) .

  3. Déterminer le module et un argument des nombres : -2 ; 5 ; \(3i\) ; \(-2i\) ; \(-1-i\) ; \(\sqrt 3+i\) ; \(\sqrt 3-3i\)

Exercice 9 : Lecture graphique

Lire le module et un argument des affixes des points de la figure :

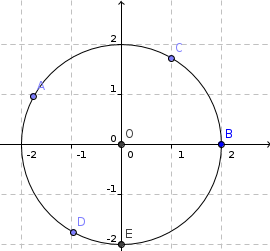
Figure

Exercice 10 : Représenter graphiquement

Dans le plan complexe muni d'un repère orthonormé \((\text O;\overrightarrow{u} ,\overrightarrow{ {v}})\) , représenter les points M d'affixe \(z\)  tels que :

  1. \(\text{arg}\left(z\right)=\dfrac{\pi } 3\)

  2. \(\text{arg}\left(z\right)=\dfrac{-2\pi } 3\)  

  3. \(\left\{\begin{matrix}\text{arg}\left(z\right)=\dfrac{\pi } 4 \\ \left|z\right|=3 \end{matrix}\right.\)  

Exercice 11 : S'aider de la représentation graphique

Dans le plan complexe muni d'un repère orthonormé \((\text O;\overrightarrow{u} ,\overrightarrow{ {v}})\) , représenter, puis déterminer le module et un argument des nombres : \(z_1=-1+i\)  , \(z_2=-1-i\)  , \(z_3=-4\)  , \(z_4=3i\)  

Exercice 12

Soit \(z=\cos \left(\dfrac{7\pi } 8 \right)+i\sin \left(\dfrac{7\pi } 8\right)\) .

  1. Donner le module et un argument de \(z\) .

  2. En déduire le module et un argument de: \(z_1=2z\) , \(z_2=\mathit{iz}\) , \(z_3=-3z\)   ,\(z_4=-3\mathit{iz}\)  , \(z_5=\overline z\)

La notation exponentielle

Exercice 13 : Mettre sous forme exponentielle

Mettre sous forme exponentielle les nombres complexes :

\(z_1=-\sqrt 3+i\)   , \(z_2=-2-2i\)  , \(z_3=-\dfrac 1 2(\sqrt 3+i)\)  , \(z_4=3-i\sqrt 3\)  , \(z_5=4+4i\)

En déduire les formes exponentielles de \(z_1z_2\) , de \(z_3z_4z_5\)  et de \(\dfrac{z_2}{z_3}\) .

Exercice 14 : Mettre sous forme algébrique

Mettre sous forme algébrique les nombres complexes :

\(z_1=4\text e^{\frac{i\pi} 2}\)  , \(z_2=\text e^{i\pi }\)  , \(z_3=2\text e^{i\frac{3\pi } 4}\)

Exercice 15 : Mettre sous forme exponentielle

Les questions sont indépendantes.

  1. On pose \(z=3-i\sqrt 3\)

    a. Déterminer l'écriture exponentielle de \(z\) .

    b. En déduire les écritures exponentielles de : \(z_1=3z\) , \(z_2=\mathit{iz}\)  , \(\text z_3=-2z\)  , \(z_4=-4\mathit{iz}\)  

  2. Soit \(z=r\text e^{i\theta }\)  (où \(r>0\) ). Déterminer l'écriture exponentielle de \(-z\) , \(\mathit{iz}\)  , \(-\mathit{iz}\)  , \(\overline z\) et \(-i\overline z\) .

  3. Soit \(a\in \mathbb{R}\)  . Déterminer l'écriture exponentielle des nombres suivants :

\(\cos a-i\text{sin}a\)   , \(\sin a+i\cos a\)  et \(-\sin a+i\cos a\)

Exercice 16 : Valeurs exactes

\(\cos \left(\dfrac{\pi }{12}\right)\)  et de \(\sin \left(\dfrac{\pi}{12}\right)\)  

Soit \(z_1=\dfrac{\sqrt 6-i\sqrt 2} 2\)  et \(z_2=1+i\).

  1. Déterminer les formes exponentielles de \(z_1\) et de \(z_2\)

  2. En déduire celle de \(\text Z=z_1z_2\)

  3. Déterminer la forme algébrique de \(Z\)

  4. En déduire la valeur exacte de \(\cos \left(\dfrac{\pi }{12}\right)\)  et de \(\sin \left(\dfrac{\pi }{12}\right)\)

Exercice 17 : Simplification d'écriture

Simplifier l'écriture du nombre suivant :

\[b=(\text e^{i\theta }-\text e^{-i\theta })^2-(\text e^{i\theta }+\text e^{-i\theta })^2\]

Exercice 18 : Retrouver des formules de trigonométrie

En utilisant la forme exponentielle, exprimer les expressions suivantes en fonction de \(\cos x\)  et de \(\sin x\) .

\(\cos \left(\dfrac{\pi } 2+x\right)\)  , \(\sin \left(\dfrac{\pi } 2-x\right)\)  , \(\cos \left(2x-\dfrac{\pi } 2\right)\)

Exercice 19 : Un calcul pas si compliqué

Déterminer le module et un argument de \(\left(\dfrac{3+i\sqrt 3}{2-2i}\right)^4\) .

Nombres complexes et géométrie

Le plan complexe est muni d'un repère orthonormé \((\text O;\overrightarrow{u} ,\overrightarrow{ {v}})\) .

Exercice 20 : Ensembles de points

Dans chacun des cas, déterminer géométriquement l'ensemble des points \(\text{M}\) dont l'affixe \(z\)  vérifie :

  1. \(\left|z-3-2i\right|=5\)

  2. \(\left|z-2-i\right|=\left|z+5-i\right|\)

  3. \(\left|z+i\right|=\left|z-1\right|\)

Exercice 21 : Ensemble de points , arguments et angles orientés de vecteurs

Pour cet exercice on utilisera la propriété suivante :

Si \(\overrightarrow{t_1}\) et \(\overrightarrow{t_2}\) sont deux vecteurs d'affixes \(z_1\)  et  \(z_2\)  non nulles, alors  \((\overrightarrow{ {t_1}},\overrightarrow{ {t_2}})=\text{arg}\left(\dfrac{z_2}{z_1}\right)\) \(\left[2\pi \right]\)

Soit A,B,C et D les points d'affixes \(z_{\text A}=1\) , \(z_{\text B}=i\) , \(z_{\text C}=-1\)  et \(z_{\text D}=-i\).

  1. Déterminer l'ensemble des points d'affixe \(z\)  tel que \(\dfrac{z+i}{z+1}\)  soit un imaginaire pur.

  2. Déterminer l'ensemble des points d'affixe \(z\)  tel que \(\text{arg}\left(z-i\right)=-\dfrac{\pi } 2+2k\pi\)  ( où \(k\in \mathbb{Z}\) )

Exercice 22 : Vecteurs orthogonaux, points alignés

Soit \(\text M\)  et \({\text M'}\)  d'affixes \(z=x+iy\)  et \(z'=x'+iy'\)  où \(x\) , \(y\) , \({x'}\) et \({y'}\)  sont des nombres réels. Montrer que :

  1. \(\overrightarrow{\text{OM}}\)  et \(\overrightarrow{\text{OM'}}\) sont orthogonaux si, et seulement si , Re( \({z'}\overline z\) )=0

  2. \(\text O\) , \(\text M\)  et \({\text M'}\)  sont alignés si, et seulement si Im( \({z'}\overline{z})=0\)

Fonctions dans les complexes

Exercice 23

Soit I le point d'affixe \(2i\)  et \(f\)  la fonction qui à tout point M d'affixe \(z\) , associe le point M' d'affixe \({z'}\)  tel que \({z'}=\mathit{iz}\).

  1. a. Déterminer l'affixe du point \({\text A'}\) , l'image par \(f\)  du point A d'affixe \(1+\sqrt 2+i\).

    b. Montrer que A, I et \({\text A'}\)  sont alignés.

  2. a. Montrer que les points M du plan tels que M, I et \({\text M'}\)  soient alignés sont sur le cercle \(\Gamma\)  de centre \(\Omega\)  d'affixe \(1+i\)  et de rayon \(\sqrt 2\) .

    b. Montrer que \(\text A\in \Gamma\).

    c. Déterminer l'ensemble \(\Gamma\) décrit par le point \({\text M'}\)  lorsque le point M décrit \(\Gamma\) .

  3. Soit \(\text B\) le point d'affixe \(2+2i\)  et \({\text B'}\)  son image par \(f\) .

    a. Montrer que \((\text{AB})\perp ({\text A'}{\text B'})\)

    b. Soit C le point d'intersection des droites \((\text{AB})\)  et \(({\text A'}{\text B'})\) . Déterminer la nature du quadrilatère \({\text{OACA}'}\) .

Exercice 24

Soit les points A et B d'affixes respectives 2 et \(-2\)   et \(f\)  la fonction qui à tout point M (différent de A) d'affixe \(z\) , associe le point M' d'affixe \({z'}\)  tel que \({z'}=\dfrac{\overline z(z-2)}{\overline z-2}\) .

  1. a. Déterminer l'affixe du point \({\text P'}\)  image par \(f\)  du point \(\text P\) d'affixe \(1+i\) .

    b. Montrer que \((\text{AP})\) // \(({\text{BP}'})\) .

    c. Montrer que \((\text{AP})\perp ({\text{PP}'})\) .

  2. Déterminer l'ensemble des points invariants par \(f\) .

    On cherche maintenant à généraliser les propriétés 1b) et 1c) pour obtenir une construction de l'image \({\text M'}\)  d'un point M quelconque du plan.

  3. a. Montrer que pour tout nombre complexe \(z\)  , ( \(z\) -2)( \(\overline z\) -2) \(\in\) \(\mathbb{R}\) .

    b. En déduire que pour tout nombre complexe distinct de 2, \(\dfrac{ {z'}+2}{z-2}\in \mathbb{R}\) .

    c. Montrer que \((\text{AM})\) // \(({\text{BM}'})\) .

  4. Soit M un point quelconque tel que \(\text M \notin (\text{AB})\) . Généraliser le résultat de la question 1c)

  5. Soit M un point distinct de A. déduire des questions précédentes une construction du point \({\text M'}\) image de M par \(f\) . Réaliser une figure pour le point Q d'affixe \(3-2i\) .