Matrices et Graphes
1. Nature d'une matrice et vocabulaire
Définitions
Définition
Soient \(m\) et \(n\) deux entiers naturels non nuls.
Une matrice de dimension \(m \times n\) est un tableau rectangulaire formé de \(m\) lignes et \(n\) colonnes de nombres réels.
Remarque
Quand on parle de dimension (ou taille) \(m \times n\), on ne calcule pas le produit !
Exemple : \(\left(\begin{array}{ccc}10 & 0 &7\\0 & 5&3\end{array}\right)\) est une matrice de \(2\) lignes et \(3\) colonnes, donc de taille \(2 \times 3\) .
Définitions
-
Une matrice ligne est une matrice formée d'une seule ligne, elle est de dimension \(1 \times n\)
-
Une matrice colonne est une matrice formée d'une seule colonne, elle est de taille \(n \times 1\).
-
Une matrice carrée d'ordre \(n\) est une matrice \(n \times n\) .
-
On note \(M_n(\mathbb{R})\) l'ensemble des matrices carrées d'ordre \(n\) à coefficients réels.
Exemples \(\left(\begin{array}{ccc}\pi & -3 &7\end{array}\right)\) est une matrice ligne, \(\left(\begin{array}{cc}\pi \\ -3 \\ 7\end{array}\right)\) est une matrice colonne, \(A=\left(\begin{array}{cc}\pi & 2 & 1 \\ \sqrt{2}&-1&0 \\ 7&3&8\end{array}\right)\) est une matrice carrée d'ordre 3. Donc \(A \in M_3(\mathbb{R})\).
Écriture générale d'une matrice
Une matrice \(A\) de taille \(m \times n\) (avec \(m \in \mathbb{N}^*\) et \(n \in \mathbb{N}^*\) ) peut s'écrire sous cette forme :
\(A=\left(\begin{array}{cc} a_{11} & a_{12} & ...& a_{1n}\\...&...&...&... \\ a_{m-1,1} & a_{m-1,2} & ... &a_{m-1,n} \\ a_{m,1} & a_{m,2}& ... & a_{m,n}\end{array}\right)\)
Les nombres \(a_{ij}\) (notés parfois \(a_{i,j}\) pour éviter les ambigüités) avec \(1 \leqslant i \leqslant m\) et \(1 \leqslant j \leqslant n\) s'appellent les coefficients de la matrice \(A\). On peut alors noter \(A=(a_{ij})_{1 \leqslant i \leqslant m,1 \leqslant j \leqslant n}\) .
Le coefficient \(a_{ij}\) est donc le nombre placé à la \(i\)-ième ligne et la \(j\)-ième colonne.
Définition
Deux matrices seront égales si et seulement si elles ont le même format et ont les mêmes coefficients aux mêmes places.
Matrices particulières
Définitions
Dans une matrice carrée d'ordre \(n\) , les coefficients \(a_{11} , a_{22}, ..., a_{nn}\) forment la diagonale principale de la matrice.
Une matrice carrée est diagonale si et seulement si ses coefficients qui ne sont pas sur la diagonale principale sont tous nuls.
Exemple \(\left(\begin{array}{cc}\pi & 0 & 0 \\ 0&-1&0 \\ 0&0&8\end{array}\right)\) est une matrice diagonale.
Définition
La matrice unité d'ordre \(n\) (ou matrice identité d'ordre \(n\) ), notée \(I_n\) , est la matrice carrée d'ordre \(n\) contenant uniquement des \(1\) sur sa diagonale principale et des \(0\) ailleurs.
Exemple \(I_2=\left(\begin{array}{cc}1 & 0 \\ 0&1\end{array}\right)\)
Définition
La matrice nulle d'ordre \(n\) , notée \(0_n\) , est la matrice carrée d'ordre \(n\) dont tous les coefficients sont nuls.
2. Opérations sur les matrices
Addition et multiplication par un réel
Définition
Si \(A=(a_{ij})\) et \(B=(b_{ij})\) sont deux matrices de même taille \(m \times n\) , leur somme \(A+B\) est définie par \(A+B=(a_{ij}+b_{ij})_{1\leqslant i \leqslant m,1 \leqslant j \leqslant n}\).
On ne peut donc ajouter que des matrices de même taille, et pour cela on ajoute les coefficients situés à la même place.
Exemple \(\left(\begin{array}{cc}2 & 4\\-1 & 10\end{array}\right)+\left(\begin{array}{cc}3 & -4\\6 & 5\end{array}\right)=\left(\begin{array}{cc}2+3 & 4+(-4)\\-1+6 & 10+5\end{array}\right)=\left(\begin{array}{cc}5 & 0\\5 & 15\end{array}\right)\)
Définition
Soit \(A=(a_{ij})_{1 \leqslant i \leqslant m,1 \leqslant j \leqslant n}\) une matrice et \(\lambda \in \mathbb{R}\). La matrice \(\lambda A\) est la matrice \((\lambda a_{ij})_{1 \leqslant i \leqslant m , 1 \leqslant j \leqslant n}\).
Multiplier une matrice par un réel revient à multiplier tous les coefficients par ce réel.
Remarques
-
On a de façon évidente \(A+B=B+A\).
-
Les règles de priorité sont les mêmes qu'avec les réels : \(2A+3B\) désigne la matrice \((2A)+(3B)\).
-
Pour tous réels \(\lambda\) et \(\mu\), on peut montrer que \(\lambda(\mu A)=(\lambda \mu)A\) et \(\lambda(A+B)=\lambda A+\lambda B\) .
-
On peut désormais définir la différence de deux matrices \(A\) et \(B\) de même taille : \(A−B=A+(−1)B\).
-
Pour toute matrice carrée \(A\) d'ordre \(n\), on a \(A+O_n=A\).
Multiplication d'une matrice ligne par une matrice colonne
Définition
Soit \(n\) un entier naturel non nul.
Soient \(A=(a_{1j})\) une matrice ligne \(1 \times n\) et \(B=(b_{i1})\) une matrice colonne \(n \times 1\) (le nombre de colonnes de \(A\) est donc égal au nombre de lignes de \(B\) ).
Alors \(A \times B=\left(\begin{array}{cc}a_{11} & a_{12} & ... & a_{1n}\end{array}\right) \times \left(\begin{array}{cc}b_{11} \\ b_{21} \\ ... \\ b_{n1}\end{array}\right)=(a_{11} \times b_{11}+a_{12}\times b_{21}+...+a_{1n}\times b_{n1})\)
Remarque
On peut donc écrire \(A \times B=(\sum_{k=1}^{k=n}a_{1k} \times b_{k1})\)
Exemple
\(A \times B=\left(\begin{array}{cc}-1 & 2 & 1\end{array}\right) \times \left(\begin{array}{cc}6 \\ 1 \\ 1\end{array}\right)=(-1 \times 6+2\times 1+1 \times 1)=(-3)\)
Remarque
On oublie pas d'écrire les parenthèses car le produit de deux matrices est une matrice.
Multiplication de deux matrices
Théorème
Le produit \(AB\) de deux matrices \(A\) et \(B\) existe si et seulement si le nombre de colonnes de \(A\) est égal au nombre de lignes de \(B\).
Définition
Soient \(A\) une matrice de taille \(m \times n\) et \(B\) une matrice de taille \(n \times p\).
Le produit \(A \times B\) ou \(AB\) est la matrice de taille \(m \times p\) dont le coefficient situé à la ligne \(i\) et la colonne \(j\) est obtenu en sommant les produits des éléments de la \(i\)-ième ligne de \(A\) par les éléments de la \(j\)-ième colonne de \(B\).
Exemples
-
Le produit d'une matrice \(2 \times 3\) par une matrice \(3 \times 3\) est une matrice \(2 \times 3\).
-
Le produit de deux matrices \(2 \times 2\) est une matrice \(2 \times 2\)
On peut, au brouillon, adopter cette présentation. De plus, on ne détaille pas le calcul des sommes :
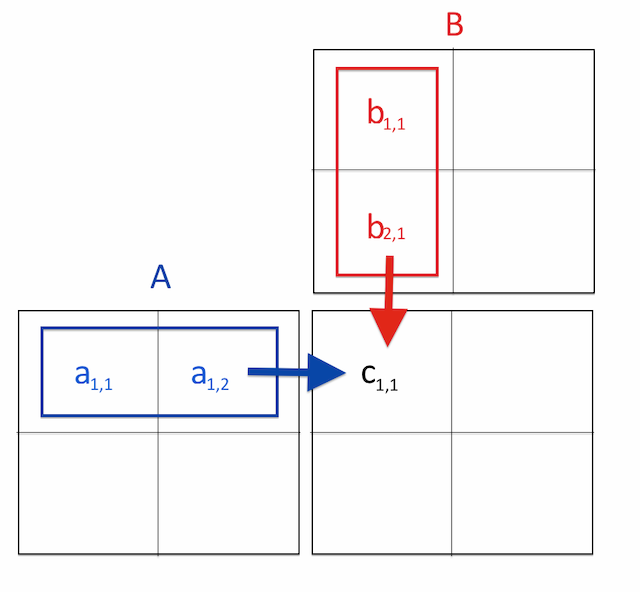
(le coefficient de la première ligne, première colonne du produit est le produit de la première ligne de la première matrice par la première colonne de la deuxième matrice : \(c_{1,1}=a_{1,1}\times b_{1,1}+a_{1,2} \times b_{2,1}\)).
Propriétés
Soient \(A\), \(B\), \(C\) des matrices carrées d'ordre \(n \in \mathbb{N}^*\).
-
Associativité : \((A \times B) \times C=A \times (B \times C)\). Ce produit se note \(A \times B \times C\) ou \(ABC\).
-
Distributivité : \(A \times (B+C)=AB+AC\) et \((A+B) \times C=AC+BC\).
-
Produit par un réel \(\lambda\) : \((\lambda A)\times B=\lambda AB\) et \(A\times(\lambda B)=\lambda AB\).
-
Soit \(I_n\) la matrice unité d'ordre \(n\) alors \(I_n \times A=A\) et \(A \times I_n=A\).
Remarque
La multiplication de matrices n'est pas commutative : en général, \(A \times B \neq B \times A\) (le produit \(AB\) peut même exister, alors que \(BA\) n'existe pas).
Exemples
Soient \(A=\left(\begin{array}{cc}1 & 2 \\ -2 & 3\end{array}\right)\) et \(B=\left(\begin{array}{cc}2 & 2 \\ -1 & 0\end{array}\right)\).
On a \(AB=\left(\begin{array}{cc}0 & 2 \\ -7 & -4\end{array}\right)\) mais \(BA=\left(\begin{array}{cc}-2 & 10 \\ -1 & -2\end{array}\right)\) donc \(AB \neq BA\) .
Remarque
Soient A , B et C des matrices carrées d'ordre \(n \in \mathbb{N}^*\).
Si \(AB=AC\), on ne peut pas en déduire que \(B=C\) (on ne peut pas "simplifier" par \(A\)).
Exemple
\(\left(\begin{array}{cc}2 & 1 \\ 4 & 2\end{array}\right) \times \left(\begin{array}{cc}4 & -2 \\ 2 & 1\end{array}\right)=\left(\begin{array}{cc}10 & -3 \\ 20 & -6\end{array}\right)\) et \(\left(\begin{array}{cc}2 & 1 \\ 4 & 2\end{array}\right) \times \left(\begin{array}{cc}5 & -5 \\ 0 & 7\end{array}\right)=\left(\begin{array}{cc}10 & -3 \\ 20 & -6\end{array}\right)\)
Remarque
Soient \(A\) et \(B\) deux matrices carrées d'ordre \(n \in \mathbb{N}^*\).
Si \(AB=O_n\) , on ne peut pas en déduire que \(A=O_n\) ou \(B=O_n\) (on ne peut pas, comme pour les nombres réels, utiliser le théorème de l'équation produit nulle).
Exemple
\(\left(\begin{array}{cc}2&1\\4&2\end{array}\right) \times \left(\begin{array}{cc}1&-3\\-2&6\end{array}\right)=\left(\begin{array}{cc}0&0\\0&0\end{array}\right)\).
Puissances entières positives de matrices
Définition
Soit \(A\) une matrice carrée d'ordre \(n \in \mathbb{N}^*\) , on notera \(A^2=A \times A\), \(A^3=A \times A \times A\), etc. Plus généralement, pour \(k \in \mathbb{N}^*\) , \(A^k\) sera le produit de \(k\) matrices toutes égales à \(A\). Par convention, on posera \(A^0=I_n\).
3. Matrices inversibles et Applications
Matrices inversibles
Propriétés
Soit \(A\) une matrice carrée d'ordre \(n\). On dit que \(A\) est inversible, s'il existe une matrice notée \(A^{-1}\) telle que \(A^{-1} \times A=A \times A^{-1}=I_n\)
La matrice \(A^{-1}\) est unique, et est appelée matrice inverse de \(A\).
Exemple : \(\left( \begin{array}{c} 1&-0.5 \\-2&1.5 \end{array} \right) \times \left( \begin{array}{c} 3&1 \\4&2 \end{array} \right) = \left( \begin{array}{c} 1&0 \\0&1 \end{array} \right)\)
et
\(\left( \begin{array}{c} 3&1 \\4&2 \end{array} \right) \times \left( \begin{array}{c} 1&-0.5 \\-2&1.5 \end{array} \right) = \left( \begin{array}{c} 1&0 \\0&1 \end{array} \right)\)
La matrice \(\left( \begin{array}{c} 3&1 \\4&2 \end{array} \right)\) est donc inversible et admet pour inverse la matrice \(\left( \begin{array}{c} 1&-0.5 \\-2&1.5 \end{array} \right)\).
Preuve de l'unicité
Supposons que \(A\) possède deux inverses, notés \(B\) et \(B'\) . On a donc \(AB=I_n\), \(AB'=I_n\), \(B A=I_n\), \(B'A=I_n\). On peut donc écrire : \(B'(AB)=B'I_n=B'\). On a aussi \((B'A)B=I_nB=B\) . Comme \(B'(AB)=(B'A)B\), on a \(B'=B\).
Matrices inversibles d'ordre 2
Définition
Soit A une matrice carrée d'ordre 2. On a donc \(A=\left( \begin{array}{c} a&b \\c&d \end{array} \right)\). Le réel \(ad-bc\) est appelé déterminant de la matrice \(A\) , et noté \(det(A)\) ou \(\Delta\) .
Exemple : Pour \(\left( \begin{array}{c} 3&1 \\4&2 \end{array} \right)\), on a \(\Delta=3 \times 2-1 \times 4=2\) .
Théorème
Soit \(A=\left( \begin{array}{c} a&b \\c&d \end{array} \right)\) une matrice carrée d'ordre 2. Alors :
-
Si \(\Delta \neq 0\) , A est inversible ; on a \(A^{−1}=\dfrac{1}{\Delta}\left( \begin{array}{c} d&-b \\-c&a \end{array} \right)\).
-
Si \(\Delta=0\), \(A\) n'est pas inversible.
Preuve
- Si \(\Delta \neq 0\) , \(A^{-1}\) existe. Soit \(B=\dfrac{1}{\Delta}\left( \begin{array}{c} d&-b \\-c&a \end{array} \right)\). On a alors \(AB=\dfrac{1}{\Delta}\left( \begin{array}{c} a&b \\c&d \end{array} \right) \times \left( \begin{array}{c} d&-b \\-c&a \end{array} \right)=\dfrac{1}{\Delta}\left( \begin{array}{c} \Delta&0 \\0&\Delta \end{array} \right) =I_2\).
De même, on vérifie que l'on a aussi \(BA=I_2\) donc \(B\) est l'inverse de \(A\).
-
Si \(\Delta=0\) , démontrons par l'absurde que \(A\) n'est par inversible :
on suppose que \(A\) admet une matrice inverse \(A'\).
Soit \(B=\left(\begin{array}{c}−c&a\\-c&a \end{array}\right)\).
On calcule \(B(AA')=BI_2=B\) et \((BA)A'=\left( \left(\begin{array}{c}−c&a\\-c&a \end{array}\right)\left( \begin{array}{c} a&b \\c&d \end{array} \right) \right)\times A'=\left(\begin{array}{c} 0&ad-bc \\0&ad-bc \end{array}\right)=0_2\) d'où \(B=0_2\) donc \(c=a=0\).
Soit \(C=\left(\begin{array}{c}d&-b\\d&-b \end{array}\right)\).
On calcule \(C(AA')=CI_2=C\) et \((CA)A'=\left( \left(\begin{array}{c}d&-b\\d&-b \end{array}\right)\left( \begin{array}{c} a&b \\c&d \end{array} \right) \right)\times A'=\left(\begin{array}{c} ad-bc&0 \\ad-bc&0 \end{array}\right)=0_2\) d'où \(C=0_2\) donc \(b=d=0\).
On en déduit que \(A=0_2\) , ce qui est absurde puisque \(O_2\) n'est pas inversible : en effet son produit par n'importe quelle matrice carrée d'ordre \(2\) valant toujours \(O_2\) , il ne peut égaler \(I_2\). Donc \(A\) n'est pas inversible.
Exemple
Soit \(A=\left( \begin{array}{c} 1&3 \\5&6 \end{array} \right)\). On a \(\Delta=1\times6-3\times5=-9\) donc \(A\) est inversible et \(A^{-1}=\dfrac{1}{-9}\left( \begin{array}{c} 6&-3 \\-5&1 \end{array} \right)=\left( \begin{array}{ccc} -\frac{2}{3}&\frac{1}{3} \\ \frac{5}{9}&-\frac{1}{9} \end{array} \right)\).
Application aux systèmes linéaires
Exemple
On considère le système linéaire d'inconnues \(x_1\) , \(x_2\) , \(x_3\) suivant :
On remarque qu'il peut s'écrire sous la forme d'un produit de matrices:
On a alors \(AX=Y\) avec \(A=\left( \begin{array}{} 2&-3&4\\1&1&-5 \\-4&3&0 \end{array} \right)\), \(X= \left( \begin{array}{} x_1\\x_2 \\x_3 \end{array} \right)\) et \(Y=\left( \begin{array}{} -1\\2 \\6 \end{array} \right)\).
L'inconnue est la matrice colonne \(X\).
Théorème
Un système linéaire à \(n\) inconnues \(x_1\) , \(x_2\) , ..., \(x_n\) qui s'écrit:
peut aussi s'écrire sous la forme \(AX=Y\) avec \(A=(a_{ij})_{1 \leqslant i \leqslant n , 1 \leqslant j \leqslant n}\) une matrice carrée d'ordre \(n\), et \(X=(x_i)\) et \(Y=(y_i)\) des matrices colonnes à \(n\) lignes.
Si \(A\) est une matrice inversible, alors \(X=A^{-1}Y\)
Preuve
Si A est inversible, \(A X =Y\) implique \(A^{−1} ( A X )= A^{−1} Y\) d'où \(( A^{−1} A) X = A^{−1} Y\) par associativité. On a donc \(X =A^{−1} Y\).
Réciproquement, si \(X =A^{−1} Y\) , alors \(A X =A A^{−1} Y =I_n Y =Y\) .
\(A^{−1} Y\) est donc l'unique solution du système écrit sous forme matricielle.