Feuille d'entraînement Olympiades 7

Exercice 1 (National Asie Pacifique 2019) - La tête aux carrés

Soit \(n\) un entier naturel, on dit que \(n\) est « décomposable en somme de carrés » s'il est égal à une somme de carrés d'entiers naturel. Par exemple \(0\), \(10\) et \(33\) admettent pour décompositions en carrés : \(0=0^2\) , \(10=3^2+1^2\) et \(33=5^2+2^2+2^2\).

Partie A : préliminaires

1. Écrire une décomposition en somme de carrés de chacun des nombres \(5\) et \(22\).

2. Ces décompositions sont-elles les seules sommes de carrés égales à \(5\) ou à \(22\) ?

3. Tout entier naturel non nul est-il décomposable en somme de carrés ?

Partie B : Avec deux carrés seulement

Dans cette partie on s'intéresse aux entiers naturels \(n\) décomposables en somme de deux carrés, c'est-à-dire pour lesquels il existe deux entiers naturels \(a\) et \(b\) tels que \(n=a^2+b^2\) .

On appelle ces entiers naturels des « nombres bicarrés ».

Par exemple, \(1\), \(18\) et \(1402\) sont des nombres bicarrés car \(1=1^2+0^2\), \(18=3^2+3^2\), \(1402=31^2+21^2.\)

1. Le nombre \(58\) est-il un nombre bicarré ?

2. Le nombre \(21\) est-il un nombre bicarré ?

3. Y a-t-il une infinité de nombres bicarrés ?

4. Dans cette question, on s'intéresse au produit de deux nombres dont chacun est un nombre bicarré.

   1. Commencer par montrer l'égalité de Lagrange, valable pour tous nombres \(a\), \(b\), \(c\) et \(d\) :

      \[\left(a^2+b^2\right)\left(c^2+d^2\right)=\left(ac+bd\right)^2+\left(ad-bc\right)^2.\]

   2. En déduire une décomposition en somme de deux carrés de \(18\times 58\).

   3. En déduire également une décomposition en somme de deux carrés du double d'un nombre bicarré.

   4. Montrer que la moitié d'un nombre pair bicarré est un nombre bicarré.

   5. \(1344\) est-il un nombre bicarré ?

   6. Existe-t-il une infinité de nombres pairs bicarrés ?

   7. Existe-t-il une infinité de nombres pairs qui ne sont pas bicarrés ?

Partie C : Avec quatre carrés

Dans cette partie on s'intéresse aux entiers naturels décomposables en sommes de carrés pour lesquels il existe une décomposition en somme de quatre carrés.

Par exemple \(43=5^2+4^2+1^2+1^2\) et \(42=5^2+4^2+1^2+0^2\)

Joseph Louis Lagrange démontra en 1770 que tout nombre entier naturel est décomposable en quatre carrés.

1. Écrire un algorithme fournissant une décomposition en quatre carrés d'un entier \(N\) lorsque cela est possible.

2. 1. Si on veut trouver une décomposition en quatre carrés du nombre \(7044\), quel est le plus grand carré susceptible d'y figurer ? Y a-t-il une décomposition de \(7044\) dans laquelle ce carré figure ?

   2. Il existe une décomposition de \(7044\) en somme des carrés de quatre nombres en progression arithmétique, dont le plus petit est \(1\). Quels sont ces quatre nombres ?

Exercice 2 (National 2004)

Soit \(\text{ABCD}\) une feuille rectangulaire de largeur \(\text{AB}=4\) et de longueur \(\text{BC}=6\).

Soit \(\text{R}\) un point de \([\text{AB}]\) (bord inférieur de la feuille) et \(\text{T}\) une point de \([\text{AD}]\) (bord droit de la feuille). On replie la feuille suivant le segment \([\text{RT}]\) et on appelle \(\text{S}\) la nouvelle position du point \(\text{A}\) (coin inférieur droit de la feuille). Voir la figure ci-dessous.

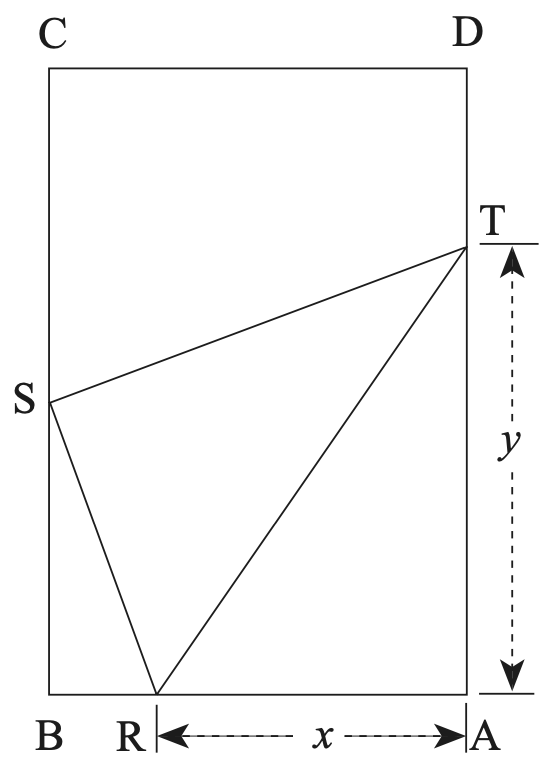
Dans tout l'exercice, on s'intéresse au cas où \(\text{S}\) est sur le segment \([\text{BC}]\) (bord gauche de la feuille).

1. Trouver les valeurs minimale et maximale de \(x\).

2. Trouver une relation entre \(x\) et \(y\) lorsque \(\text{S}\) se déplace sur \([\text{BC}]\).

3. Trouver la valeur de \(x\) pour laquelle la partie repliée (triangle \(\text{SRT}\)) est minimale. Quelle est alors la nature du triangle \(\text{AST}\) ?