Feuille d'entraînement Olympiades 6

Exercice 1 (National 2020) - Ensembles Surprenants

On désigne par \(\mathbb{N}^*\) l'ensemble des entiers naturels non nuls.

Dans tout l'exercice, les ensembles considérés sont des sous-ensembles finis non vides de \(\mathbb{N}^*\).

Si \(\text{A}\) est un tel ensemble, on désigne par \(\text{P(A)}\) le produit des éléments de \(\text{A}\) et par \(\text{C(A)}\) la somme des carrés des éléments de \(\text{A}\).

Par exemple, si \(\text{A} = \left\{1, 2, 5 \right\}\), alors \(\text{P(A)} = 1 \times 2 \times 5 = 10\) et \(\text{C(A)} = 12 + 22 + 52 = 30\).

On dit qu'un ensemble fini \(\text{A}\) est surprenant si \(\text{P(A)} = \text{C(A)}\).

1. Deux exemples.

   a. L'ensemble \(\left\{1, 2, 3, 2020\right\}\) est-il surprenant ?

   b. L'ensemble \(\left\{6, 15, 87\right\}\) est-il surprenant ?

2. On considère un sous-ensemble fini \(\text{A}\) de \(\mathbb{N}^*\) tel que \(\text{P(A)} \geq 5\).

   a. Quels sont les nombres \(x\) vérifiant l'égalité \(x\text{P(A)}\)=\(\text{P(A)}-1+x^2\) ?

   b. Montrer que le nombre \(\text{P(A)} - 1\) n'appartient pas à \(\text{A}\).

   c. On note \(\text{A'}\) l'ensemble obtenu en ajoutant l'entier \(\text{P(A)} - 1\) à l'ensemble \(\text{A}\). En d'autres termes:

   \(\text{A'} = \text{A} \cup \left\{\text{P(A)}-1\right\}\)

   Exprimer \(\text{P(A')} - \text{C(A')}\) en fonction de \(\text{P(A)} - \text{C(A)}\).

   d. En déduire que si \(\text{P(A)} > \text{C(A)}\), on peut trouver un ensemble surprenant \(\text{B}\) contenant \(\text{A}\).

   e. Trouver un ensemble surprenant contenant l'ensemble \(\left\{3, 4, 9\right\}\).

3. On considère à nouveau un sous-ensemble fini \(\text{A}\) de \(\mathbb{N}^*\) tel que \(\text{P(A)} \geq 5\).

   a. Prouver que le nombre \(\text{P(A)} - 2\) n'appartient pas à \(\text{A}\).

   b. En déduire que si \(\text{P(A)} < \text{C(A)}\), on peut trouver un ensemble surprenant \(\text{B}\) contenant \(\text{A}\).

4. En déduire finalement que, pour tout sous ensemble fini non vide \(\text{A}\) de \(\mathbb{N}^*\), on peut trouver un ensemble surprenant \(\text{B}\) contenant \(\text{A}\).

5. Montrer qu'on peut trouver un ensemble surprenant ayant 67 éléments et contenant \(\text{A} = \left\{1, 2, 5\right\}\).

Exercice 2 (National 2020) - Poteaux

Sur un terrain de jeu sont alignés quatre poteaux, plantés en \(\text{A}\), \(\text{B}\), \(\text{C}\) et \(\text{D}\) dans cet ordre.

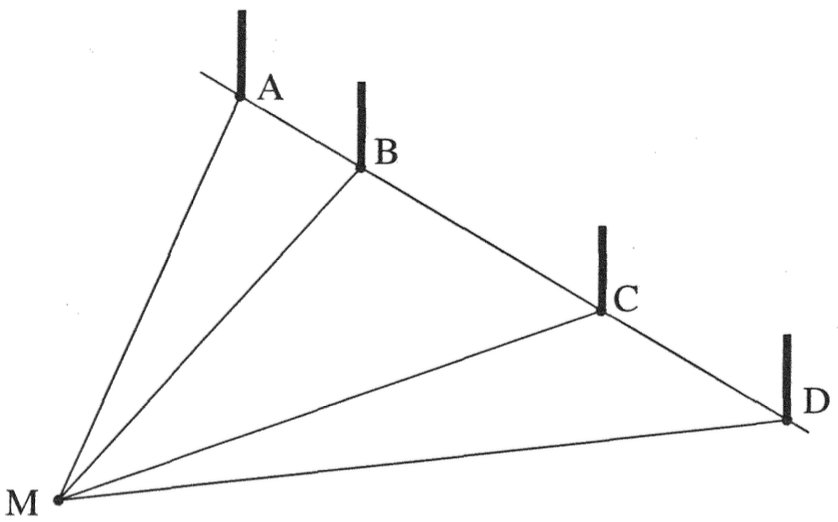
Ces poteaux déterminent trois buts de largeurs :

\(AB=1\), \(BC=2\), \(CD= d\), où \(d\) est une longueur donnée.

Déterminer l'ensemble des points M du terrain d'où l'on voit les trois buts sous des angles \(\widehat{AMB}\), \(\widehat{BMC}\) et \(\widehat{CMD}\) égaux.