Feuille d'entraînement Olympiades 4

Exercice 1 (National 2012) - Nombres digisibles

On dit qu'un nombre entier est digisible lorsque les trois conditions suivantes sont vérifiées:

• aucun de ses chiffres n'est nul ;

• il s'écrit avec des chiffres tous différents ;

• il est divisible par chacun d'eux.

Par exemple,

• 24 est digisible car il est divisible par 2 et par 4 ;

• 324 est digisible car il est divisible par 3, par 2 et par 4 ;

• 32 n'est pas digisible car il n'est pas divisible par 3.

On rappelle qu'un nombre entier est divisible par 3 si et seulement si la somme de ses chiffres est divisible par 3.

1. Proposer un autre nombre digisible à deux chiffres.
2. Proposer un nombre digisible à quatre chiffres.

3. Soit \(n\) un entier digisible s’écrivant avec un 5.

   1. Démontrer que 5 est le chiffre de ses unités.

   2. Démontrer que tous les chiffres de \(n\) sont impairs.

   3. Démontrer que \(n\) s’écrit avec au plus quatre chiffres.

   4. Déterminer le plus grand entier digisible s'écrivant avec un 5.

4. Soit \(n\) un entier digisible quelconque.

   1. Démontrer que \(n\) s’écrit avec au plus sept chiffres.

   2. Si \(n\) s'écrit avec sept chiffres, dont un 9, déterminer les chiffres de \(n\).

   3. Déterminer le plus grand entier digisible.

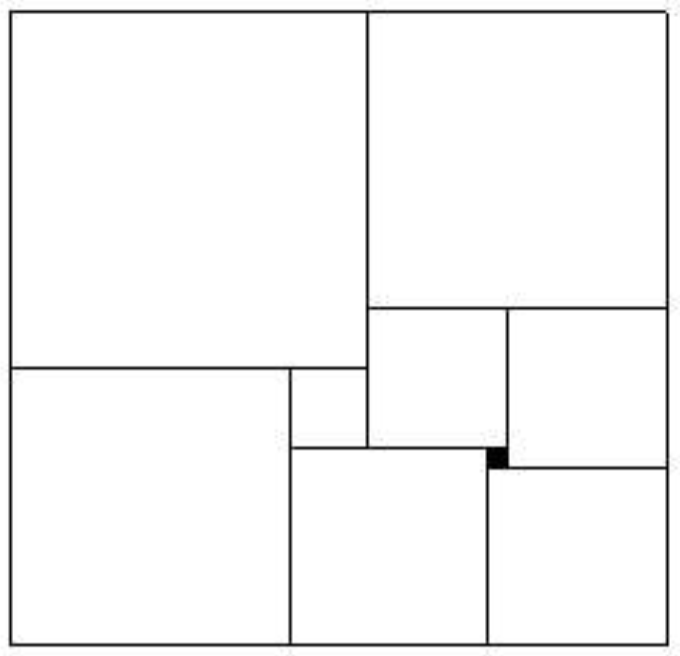
Exercice 2

Le rectangle ci-dessous est pavé par 9 carrés. Le carré noir a pour côté une unité. Quelles sont les dimensions du rectangle ?