Petit Devoir : Probabilités 20-21

L'usage de la calculatrice est autorisé.

Un soin particulier sera apporté à la rédaction et aux justifications

Durée : 30 min

Exercice 1 (3 points)

Vrai ou faux (pour chaque question : 0,5 si juste / -0,5 si faux / 0 si pas de réponse)

AffirmationsCorrigé

1. Si \(\text P(\text A)=1\), alors \(\text A\)  et \(\text B\)  sont indépendants.
2. Si A \(\subset\) B, alors \(\text A\)  et \(\text B\)  sont indépendants.
3. Si \(\overline{\text A}\)  et \(\overline{\text B}\)  sont indépendants, alors \(\overline{\text A}\)  et \(\text B\) le sont aussi.
4. Si \(\text P(\text A)=0,3\)  et \(\text P(\text B)=0,6\)  et  \(\text P(\text A\cap \text B)=0,18\)  , alors \(\text A\) et \(\text B\) sont indépendants.
5. Si \(\text P(\text A)=0,{37}\)  et \(\text P(\text A\cap \text B)=0,2\) , alors \(\text P(\text A\cup \text B)=0,{57}\)
6. Si A et B sont indépendants, \(\text P(\text A)=0,3\)  et \(\text P(\text B)=0,2\) , alors \(\text P(\overline{\text A}\cap \overline{\text B})=0,{94}\)

1. V
2. V
3. V
4. V
5. F
6. F

Exercice 2 (4 points)

SujetCorrigé

Une compagnie d'assurance auto propose deux types de contrat :

• un contrat « Tous risques » ;
• un contrat « de base ».

En consultant le fichier clients de la compagnie, on recueille les données suivantes :

• 60% des clients possèdent un véhicule récent (moins de 5 ans). Les autres clients ont un véhicule ancien ;
• parmi les clients possédant un véhicule récent, 70% ont souscrit au contrat « Tous risques » ;
• parmi les clients possédant un véhicule ancien, 50% ont souscrit au contrat « Tous risques ».

On considère un client choisi au hasard.

D'une manière générale, la probabilité d'un événement \(\text A\)  est notée \(\text P(\text A)\)  et son événement contraire est noté \(\bar{\text A}\) .

On note les événements suivants :

• \(\text R\) : « le client possède un véhicule récent » ;

• \(\text T\) : « le client a souscrit au contrat « Tous risques ».

• Donner, sans justifications, l'arbre pondéré de probabilité traduisant les données de l'exercice.

• Calculer la probabilité qu'un client pris au hasard possède un véhicule récent et ait souscrit au contrat « Tous risques ».

• Calculer \(\text P(\text T)\)

1. Arbre de probabilités :

   

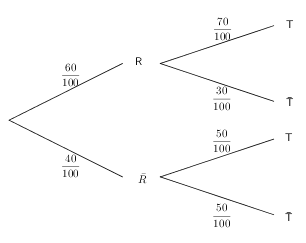
2. \(\text P(\text R{\cap}\text T)=\text P(\text R)\times \text P_{\text R}(\text T)=\dfrac{60}{100}\times \dfrac{70}{100}=\dfrac{42}{100}\)

3. \(\text R{\cap}\text T\)  et \(\bar{\text R}{\cap}\text T\)  forment une partition de \(\text T\), d'après la formule des probabilités totales, on a :

   \(\text P(\text T)=\text P(\text R{\cap}\text T)+\text P(\bar{\text R}{\cap}\text T)=\dfrac{42}{100}+\dfrac{40}{100}\times \dfrac{50}{100}=\dfrac{62}{100}\).

Exercice 3 (2 points)

Ci-dessous, on a représenté dans un tableau la répartition des licenciés d'un club de sport.

	\(\text {Jeune}\)	\(\text {Adulte}\)	\(\text {Total}\)
\(\text {Homme}\)	34	46	80
\(\text {Femme}\)	68	92	160
\(\text {Total}\)	102	138	240

On prélève au hasard la fiche de l'un des licenciés.

On considère les événements:

\(\text F\) : « Le licencié est une femme »;

\(\text A\) : « Le licencié est un adulte ».

SujetCorrigé

Justifier que les événements \(\text A\)  et \(\text F\)  sont indépendants.

Avec le tableau, on calcule :

\(\text P_{\text F}(\text A)=\dfrac{\text P(\text A{\cap}\text F)}{\text P(\text F)}=\dfrac{\text{card}(\text A{\cap}\text F)}{\text{card}(\text F)}=\dfrac{92}{160}=\dfrac{23}{40}\) et \(\text P(\text A)=\dfrac{\text{card}(\text A)}{\text{card}(\Omega)}=\dfrac{138}{240}=\dfrac{23}{40}\).

On a donc \(\text P_{\text F}(\text A)=\text P(\text A)\)  et les évènements \(\text A\)  et \(\text F\)  sont bien indépendants.