Aller au contenu

Petit Devoir sur le Produit Scalaire 18-19

L'usage de la calculatrice est autorisé.

Durée: 30 min

Exercice 1

Le trapèze rectangle de la figure ci-dessous est tel que : AB=7, AD=4 et CD=4

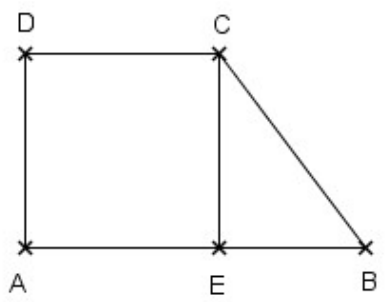
Donner sans justification les valeurs exactes des produits scalaires suivants:

  1. \(\overrightarrow{\text{EB}}\cdot \overrightarrow{\text{CD}}\)

  2. \(\overrightarrow{\text{DA}}\cdot \overrightarrow{\text{AC}}\)

  3. \(\overrightarrow{\text{DE}}\cdot \overrightarrow{\text{CA}}\)

  4. \(\overrightarrow{\text{BA}}\cdot \overrightarrow{\text{BC}}\)

  5. \(\overrightarrow{\text{CD}}\cdot \overrightarrow{\text{CB}}\)

  6. \(\overrightarrow{\text{DA}}\cdot \overrightarrow{\text{CB}}\)

  1. \(\mathit{EB}=\mathit{AB}-\mathit{AE}=7-4=3\)

    Les vecteurs \(\overrightarrow{\mathit{EB}}\) et \(\overrightarrow{\mathit{CD}}\) sont colinéaires et de sens contraires, donc :

    \(\overrightarrow{\mathit{EB}}\cdot \overrightarrow{\mathit{CD}}=-\mathit{EB}\times \mathit{CD}=-3\times 4=-12\)

  2. \(\overrightarrow{\text{DA}}\cdot \overrightarrow{\text{AC}}=-\text{DA}^2=-16\)

  3. \({AECD}\) est un carré, donc ses diagonales sont perpendiculaires, donc les vecteurs \(\overrightarrow{\mathit{DE}}\) et \(\overrightarrow{\mathit{CA}}\) sont orthogonaux.

    \(\overrightarrow{\mathit{DE}}\cdot \overrightarrow{\mathit{CA}}=0\) .

  4. \(E\) est le projeté orthogonal de \(C\) sur \((BA)\). Donc \(\overrightarrow{\mathit{BA}}\cdot \overrightarrow{\mathit{BC}}=\overrightarrow{\mathit{BE}}\cdot \overrightarrow{\mathit{BA}}=3\times 7=21\).

  5. \(\overrightarrow{\text{CD}}\cdot \overrightarrow{\text{CB}}=-\text{CD}\times \text{EB}=-4\times 3=-12\)

  6. \(D\) est le projeté orthogonal de \(C\) sur \((DA)\) et \(A\) est le projeté orthogonal de \(B\) sur \((DA)\).

    D'où \(\overrightarrow{\mathit{DA}}\cdot \overrightarrow{\mathit{CB}}=\overrightarrow{\mathit{DA}}\cdot \overrightarrow{\mathit{DA}}=4\times 4=16\).

Exercice 2

Soit un repère \((\text O;\vec{\imath};\vec{\jmath})\) orthonormé d'unité \(1\) cm.

Soient les points \(A\left(\frac 1 2;1\right)\), \(B\left(3,-\frac 1 2\right)\)  et \(C\left(\frac 5 2;\frac 5 2\right)\) .

  1. a) Calculer les longueurs \(AB\) , \(AC\)  et \(\overrightarrow{\mathit{AB}}\cdot\overrightarrow{\mathit{AC}}\).

    b) En déduire \(\cos (\widehat {BAC})\)  puis une mesure de \(\widehat {BAC}\)  au centième de degré.

  2. Soit \(H\) le pied de la hauteur issue de \(B\)  dans \(ABC\).

    Calculer \(AH\)  puis arrondir \(AH\) au millimètre.

  1. a) \(\overrightarrow{\text{AB}}\) \(\left(\begin{matrix}\frac 5 2\\-\frac 3 2\end{matrix}\right)\)  \(\Rightarrow \text{AB}=\frac 1 2\sqrt{34}\)

    \(\overrightarrow{\text{AC}} \left(\begin{matrix}2\\\frac 3 2\end{matrix}\right)\)  \(\Rightarrow\) \(\text{AC}=\frac 5 2\)

    Avec la formule du produit scalaire de deux vecteurs on obtient: \(\overrightarrow{\text{AB}}\cdot \overrightarrow{\text{AC}}=\frac{10} 2-\frac 9 4=\frac{11} 4\).

    b) On a aussi \(\overrightarrow{\text{AB}}\cdot \overrightarrow{\text{AC}}=\text{AB}\times \text{AC}\times \text{cos}(\widehat {\text{BAC}})\)  d'où \(\frac{11} 4=\frac 5 4\times \sqrt{34}\times \text{cos}(\widehat {\text{BAC}})\)

    D'où \(\text{cos}(\widehat {\text{BAC}})=\frac{11}{5\sqrt{34}}\) et \(\widehat{\text{BAC}}{\approx}67.83^{\circ }\).

  2. \(\overrightarrow{\text{AB}}\cdot \overrightarrow{\text{AC}}=\overrightarrow{\text{AH}}\cdot \overrightarrow{\text{AC}}=\text{AH}\times \text{AC}\) d'où \(\text{AH}=\frac{\frac{11} 4}{\frac 5 2}=\frac{11}{10}=1.1\) cm.