Aller au contenu

Devoir sur les suites

L'usage de la calculatrice est autorisé mais le prêt ou l'échange sont interdits.

Durée: 55 min

Exercice 1

Dire si les propriétés suivantes sont vraies, fausses ou si l'on ne peut rien dire (on justifiera ses dires, éventuellement à l'aide d'un dessin).

  1. Une suite \((v_n)\) qui vérifie, pour tout \(n \in \mathbb{N}^*\), \(\dfrac{v_{n+1}}{v_n}<1\)  est strictement décroissante.

  2. Toute suite qui admet une limite finie est bornée (hors programme spécialité maths en 1ière).

  3. Toute suite non majorée tend vers +\({\infty}\) (hors programme spécialité maths en 1ière).

  1. La suite \(v_n=-\frac 1 n\)  contredit clairement l'affirmation, donc FAUX.

    \(\dfrac{v_{n+1}}{v_n}=\dfrac n n+1=1-\dfrac 1{n+1}<1\)  et pourtant \(x \mapsto -\dfrac 1 x\)  est une fonction croissante soit \((v_n)\) croissante.

  2. L'affirmation est VRAIE:

    Si une suite admet une limite finie \(\alpha\), alors, à partir d'une certaine valeur \(n_0\) , les termes de la suite sont proches de la limite, donc il existe \(\varepsilon\)\({\in}\mathbb{R}\)+ tel que pour \(n>n_0\), \(u_n \in ]\alpha-\varepsilon \mathrm ;\alpha+\varepsilon[\).

    Il reste a déterminer le maximum et le minimum de \((u_n)\)  pour \(n\leqslant n_0\)  et à conclure.

    Un dessin supporte très bien ce type de raisonnement.

  3. La suite \(u_n=n\times (-1)^n\)  contredit l'affirmation, donc FAUX.

    Pour \(n\)  pair, \(\lim\limits_{n \to +\infty }u_n=+\infty\)  et pour \(n\)  impair, \(\lim\limits_{n \to +\infty}u_n=-\infty\) . Donc \((u_n)\) n'est pas majorée, mais ne tend pas pour autant vers +\({\infty}\).

Exercice 2

Aux entreprises Crbn et Cie, les employés ont le choix entre deux contrats : le salaire initial est toujours de 1000€ par mois, puis une augmentation de 10€ tous les mois pour le contrat A, et une augmentation de 0,5% tous les mois pour le contrat B.

  1. On appelle \(a_n\)  le salaire mensuel d'un employé au bout de \(n\) mois avec le contrat \(\text A\)  et \(b_n\)  avec le contrat \(\text B\). Exprimer \(a_n\) et \(b_n\) en fonction de \(n\) .

  2. On propose à Saad B. un Contrat à Durée Déterminée de 18 mois. Quel contrat doit-il choisir ?

  3. Inès M. et Lina E.  ont passé 40 ans dans l'entreprise, mais Inès avait le contrat A et Lina le contrat B. Quelles sommes ont-elles gagné en tout ?

  4. Au bout de combien de temps le salaire de Lina a-t-il dépassé celui d'Inès ?

  1. On a \(a_n=1000+10n\)  (suite arithmétique de raison 10) et \(b_n=1000\times (1,005)^n\)  (suite géométrique de raison \(1+\frac{0,5}{100}=1,005\) ).

  2. Le salaire du 18ème mois peut correspondre à \(a_{17}\)  ou \(b_{17}\) .

    On a \(a_{17}=1170\)€  et \(b_{17}=1000\times (1,005)^{17}{\approx}1088,5\)€.

  3. Au bout de 40 ans:

    \(a_0+a_1+\ldots +a_{479}\)  pour Inès et \(b_0+b_1+\ldots +b_{479}\) pour Lina, on calcule donc les sommes des termes d'une suite arithmétique et d'une suite géométrique:

    \(a_0+a_1+\ldots +a_{479}=\dfrac{480\times (a_0+a_{479})} 2=240(1000+5790)=1629600\)€.

    \(b_0+b_1+\ldots +b_{479}=\dfrac{b_0(1-1,005^{480})}{1-1,005}{\approx}1991491\)€.

  4. Avec la calculatrice, soit en déroulant la table, soit avec un petit algorithme du style:

    a=1010
b=1005
n=1
Tant que a>b:
    a=a+10
    b=b*1.005
    n=n+1
FinTQ
Afficher n

    On trouve \(n=253\).

Exercice 3

La suite \((u_n)\)  est définie pour tout entier naturel \(n\)  non nul par \(u_{n+1}=\dfrac{2u_n} n\)  et \(u_1=2\).

On admettra que pour tout entier naturel \(n\geqslant 1\) , \(u_n>0\).

  1. Calculer \(u_2\)  et \(u_3\)  en détaillant.

  2. Etudier les variations de la suite \((u_n)\) .

  3. Ecrire un programme en python qui permet de déterminer le plus petit entier naturel \(n>3\)  tel que \(u_n<10^{-10}\).

  1. \(u_2=\dfrac{2u_1} 1=4\)  et \(u_3=\dfrac{2u_2} 2=4\) .

  2. On a \(u_n>0\), on calcule \(\dfrac{u_{n+1}}{u_n}=\dfrac 2 n\) et \(\dfrac 2 n<1\) pour \(n\geqslant 2\), donc \((u_n)\) est décroissante.

  3. Programme en python:

    u=2
n=1
while u>=10**{-10}
    u=2u/n
    n=n+1
print(n)

Exercice 4 Le tapis de Sierpinski

On dispose d'un carré de côté 1.

Etape 1: On partage le carré en 9 carrés identiques, et on colorie le carré central.

Etape 2: Les carrés blancs sont à leur tour partagés en 9 carrés, et on colorie les carrés centraux.

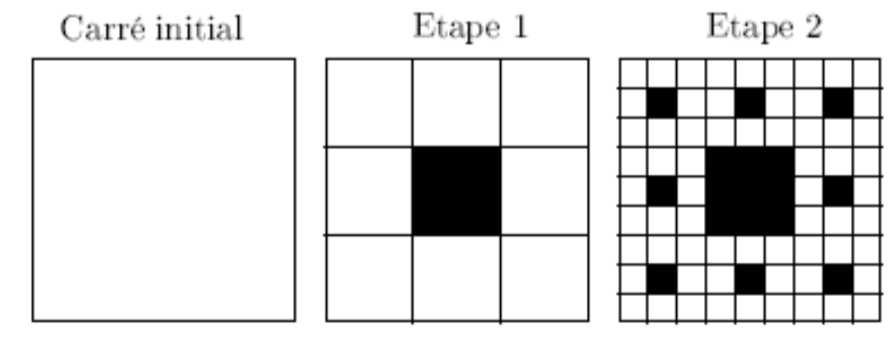
Ainsi de suite...

On note \(\text A_n\)  l'aire coloriée à la \(n\)-ième étape \(n \in \mathbb{N}^*\).

  1. Déterminer \(\text A_1\)  et \(\text A_2\) .

  2. Justifier que pour tout \(n \in \mathbb{N}^*\), \(\text A_{n+1}=\dfrac 1 9+\dfrac 8 9\text A_n\) .

  3. On pose \(u_n=\text A_n-1\) .

    1. Montrer que la suite \((u_n)\) est géométrique, préciser sa raison et son premier terme.

    2. Exprimer \(u_n\) et \(\text A_n\) en fonction de \(n\) .

  1. En lisant directement sur le dessin:

    \(\text A_1=\left(\dfrac 1 3\right)^2=\dfrac 1 9\) et \(\text A_2=\text A_1+\dfrac{8\times1}{81}=\dfrac{17}{81}\)

  2. On a \(\text A_{n+1}=\text A_n+\dfrac 1 9(1-\text A_n)=\dfrac 1 9+\frac 8 9\text A_n\)

  3. a) On a \(u_{n+1}=\text A_{n+1}-1=\dfrac 1 9+\dfrac 8 9\text A_n-1=-\dfrac 8 9+\dfrac 8 9\text A_n=\dfrac 8 9(\text A_n-1)=\dfrac 8 9u_n\) .

    \((u_n)\)  est donc géométrique de raison \(\dfrac 8 9\)  et de premier terme \(u_1=\text A_1-1=\dfrac 1 9-1=-\dfrac 8 9\) .

    b) On a \(u_n=-\dfrac 8 9\left(\dfrac 8 9\right)^{n-1}=-\left(\dfrac 8 9\right)^n\) pour \(n>0\) .

    D'où \(\text A_n=u_n+1=1-\left(\dfrac 8 9\right)^n\).

Exercice 5 (bonus)

Soit la suite définie par \(a_{m+n}=a_m+a_n+mn\) et \(a_1=1\).

Déterminer \(a_{100}\) et expliquer votre méthode.

\(a_1=1\)

\(a_2=a_1+a_1+1 \times 1=3\)

\(a_4=a_2+a_2+2\times 2=10\)

\(a_8=a_4+a_4+4\times 4=36\)

\(a_{16}=a_8+a_8+8\times 8=136\)

\(a_{32}=a_{16}+a_{16}+16\times 16=528\)

\(a_{64}=a_{32}+a_{32}+32\times 32=2080\)

\(a_{96}=a_{64}+a_{32}+64\times 32=4656\)

\(a_{100}=a_{96}+a_4+96\times 4=5050\)