Aller au contenu

Des suites et une pincée de fonctions

L'usage de la calculatrice est obligatoire.

Durée: 1h55

Exercice 1

Dans chacun des cas, déterminer \(u_0\)  ou \(u_1\)  ( si la suite n'est définie que pour \(n>0\) ) et exprimer \(u_{n+1}\)  en fonction de \(u_n\).

  1. \(u_n=4\times 3^{n-3}\)   
  2. \(u_n=1\times 2\times 3\times \ldots \times n\)   
  3. \(u_n=2n-3\)

  1. \(u_n=4\times 3^{n-3}=4\times 3^{-3}\times 3^n=\dfrac 4{27}\times 3^n\) s'écrit sous la forme d'une suite géométrique de raison 3.

    D'où \(u_{n+1}=3u_n\) .

  2. \(u_n=1\times 2\times 3\times \ldots \times n\)  donc \(u_{n+1}=1\times 2\times 3\times \ldots \times n\times (n+1)\) , d'où \(u_{n+1}=(n+1)u_n\) .

  3. \(u_n=2n-3=-3+2n\)  s'écrit sous la forme d'une suite arithmétique de raison 2.

    D'où \(u_{n+1}=u_n+2\) .

Exercice 2

Soit \((u_n)\)  la suite définie par \(u_n=\dfrac{3+\text{sin}n}{4-\text{sin}n}\).

Indiquer si la suite est minorée, majorée ou bornée.

On a \(-1\leqslant \text{sin}n\leqslant 1\)  donc \(2\leqslant 3+\text{sin}n\leqslant 4\) et \(3\leqslant 4-\text{sin}n\leqslant 5\)  \(\Rightarrow\) \(\dfrac 1 5\leqslant \dfrac 1{4-\text{sin}n}\leqslant \dfrac 1 3\)  (décroissance de \(x \mapsto \dfrac 1 x\) )

D'où \(\dfrac 2 5\leqslant \dfrac{3+\text{sin}n}{4-\text{sin}n}\leqslant \dfrac 4 3\).

Conclusion: \((u_n)\)  est minorée par \(\dfrac 2 5\) , majorée par \(\dfrac 4 3\) et donc bornée.

Exercice 3 Utilisation de la calculatrice

Soit \((u_n)\)  la suite définie par \(u_0=4\) et \(u_{n+1}=5n^2+(-1)^n\times u_n\)

Déterminer \(u_{50}\).

Avec une habile utilisation de la calculatrice, on trouve \(u_{50}=241\) .

Exercice 4

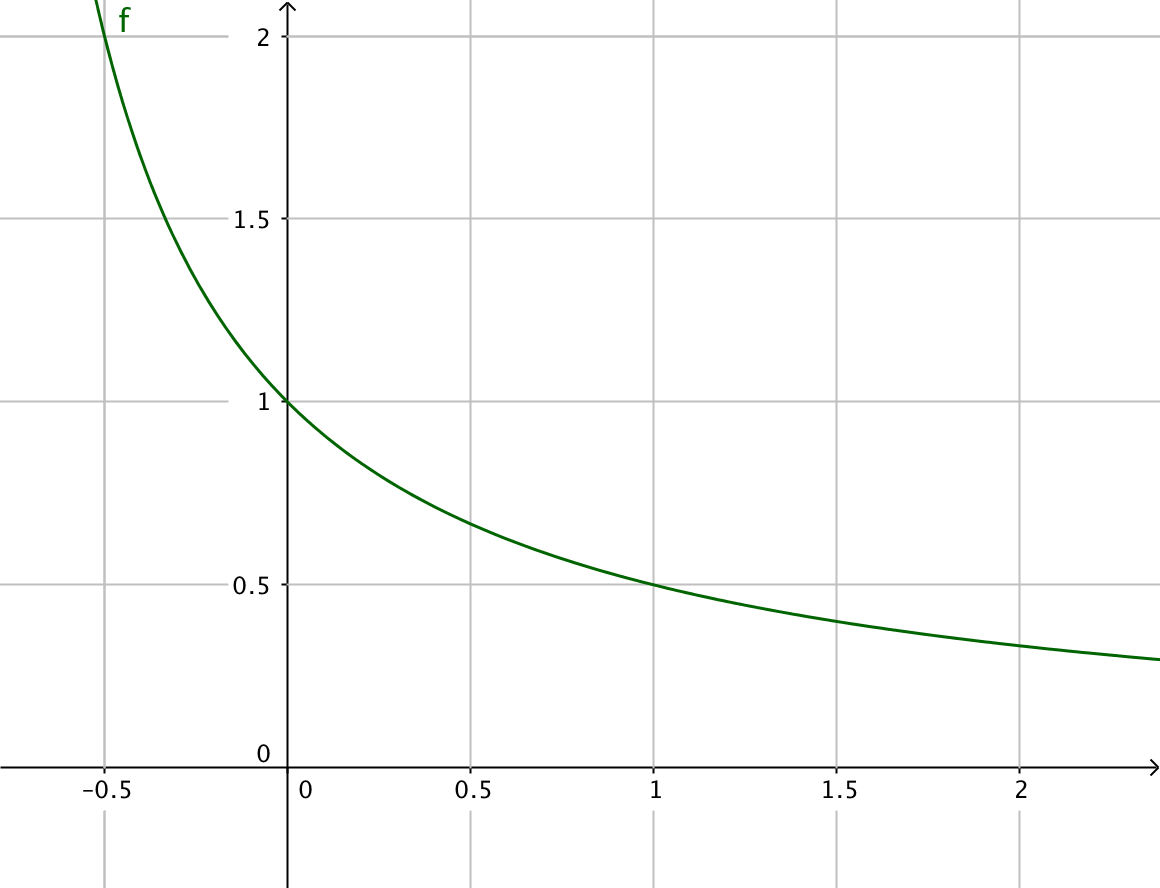
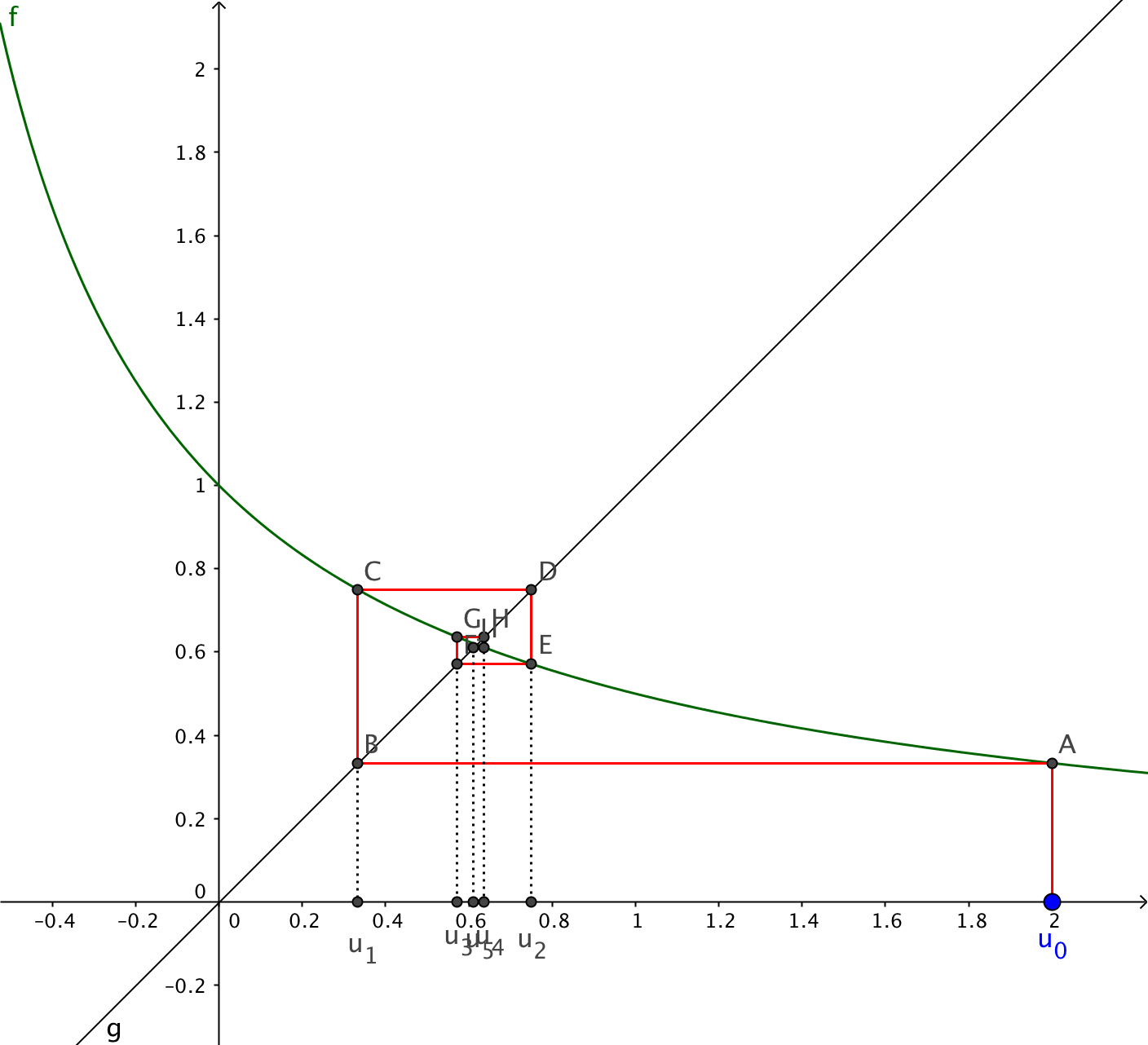
Représenter ci-dessous en abscisse les 6 premiers termes de la suite \((u_n)\)  définie par \(\left\{\begin{matrix}u_{n+1}=\dfrac 1{u_n+1}\\u_0=2\end{matrix}\right.\).

Exercice 5

Déterminer le sens de variation de la suite \((u_n)\)  définie par \(u_n=n\times \left(\dfrac 1 2\right)^n\).

\(u_n=n\times \left(\dfrac 1 2\right)^n\) . Les termes de cette suite étant strictement positifs pour \(n>0\) , on calcule:

\(\dfrac{u_{n+1}}{u_n}=\dfrac 1 2\dfrac{n+1} n=\dfrac 1 2+\dfrac 1{2n}\)  or \(\dfrac 1{2n}<\dfrac 1 2\)  pour \(n>1\)  d'où \(\dfrac{u_{n+1}}{u_n}<1\)  et \((u_n)\)  décroissante.

Exercice 6

Martin a le projet de partir 6 mois en voyage à la recherche de bons spots de surf. Pour cela, il souhaite acquérir un van et l'aménager.

Il estime le coût final de son véhicule à 15 000€.

Le 1er janvier 2014, il dépose 6 000€ sur un compte-épargne à intérêts composés rémunéré à 2,5 % par an. Il décide de plus de s'astreindre à déposer chaque 1er janvier des années suivantes 800€ sur ce compte.

On pose \(u_n\)  la somme disponible sur son compte le 1er janvier de l'année \(2014+n\) . Les résultats seront, au besoin, arrondis au centime d'euro.

  1. Justifier que, pour tout \(n\in \mathbb{N}\) , \(u_{n+1}=1,025u_n+800\).

  2. La suite \((u_n)\)  est-elle arithmétique ? géométrique ? Justifier.

  3. Soit \((v_n)\)  la suite définie pour tout \(n\in \mathbb{N}\)  par \(v_n=u_n+32000\) .

    a. Démontrer que la suite \((v_n)\)  est géométrique ; on précisera la raison et le premier terme.

    b. En déduire l'expression de \(v_n\) puis de \(u_n\)  en fonction de \(n\) .

  4. On suppose pour la suite que \(u_n=38000\times 1,025^n-32000\) .

    a. Étudier les variations de \((u_n)\) .

    b. Déterminer à quelle date il pourra partir.

  5. On souhaite écrire un algorithme affichant pour tout entier naturel \(n\)  donné, tous les termes de la suite du rang \(0\)  au rang \(n\) .

    Parmi les 3 algorithmes suivants, lequel convient ?

    On indiquera pourquoi les deux autres ne conviennent pas.

  1. Multiplier par 1,025 c'est multiplier par \(1+\dfrac{2,5}{100}\) , ce qui correspond à des intérêts composés de 2,5%. L'ajout de 800€ correspond à la somme déposée chaque 1ier janvier.

  2. On a \(u_0=6000\) , \(u_1=6950\) , \(u_2=7923,75\).

    \(u_1-u_0\neq u_2-u_1\)  donc \((u_n)\)  n'est pas une suite arithmétique.

    \(\dfrac{u_1}{u_0}\neq \dfrac{u_2}{u_1}\)  donc \((u_n)\)  n'est pas une suite géométrique.

  3. a. \(v_n=u_n+32000\)    \(\Rightarrow\) \(v_{n+1}=u_{n+1}+32000\)  

    \(\quad \Rightarrow\) \(v_{n+1}=1,025u_n+800+32000\)

    \(\quad \Rightarrow\) \(v_{n+1}=1,025u_n+32800\)

    \(\quad \Rightarrow\) \(v_{n+1}=1,025(u_n+32000)\)

    \(\quad \Rightarrow\) \(v_{n+1}=1,025v_n\)

    \((v_n)\)  est donc une suite géométrique de raison 1,025 et de premier terme \(v_0=u_0+32000=6000+32000=38000\)

    b. Avec ce qui précède, \(v_n=38000\times 1,025^n\)  et \(u_n=v_n-32000=38000\times 1,025^n-32000\)

  4. a. \(u_{n+1}-u_n=38000\times (1,025^{n+1}-1,025^n)\)  soit \(u_{n+1}-u_n=38000\times 1,025^n\times 0,025\).

    Cette quantité étant strictement positive, \((u_n)\)  est une suite strictement croissante.

    b. Avec la calculatrice, à partir de \(n=9\) . Il pourra donc partir le 1ier Janvier 2023.

  5. L'algorithme 3 convient tout à fait.

    Dans l'algorithme 2, on calcule les termes de la suite \((v_n)\), alors que dans l'algorithme 3 on affiche uniquement le dernier terme calculé.

Exercice 7

Soit les suites \((u_n)\)  et \((v_n)\)  définies par \(v_n=-\frac 1{2^n}\) et \(u_n=v_n+6n\) .

Calculer \(S= \sum _{\text i=0}^{\text i=20}v_{\text i}\) et \(T=\sum _{\text i=0}^{\text i=20}u_{\text i}\).

\(v_n\)  peut être récrite sous la forme \(v_n=-1\times \left(\dfrac 1 2\right)^n\) , \((v_n)\)  est donc une suite géométrique de premier terme \(v_0=-1\)  et de raison \(\dfrac 1 2\) .

D'où \(\text S=v_0\times \dfrac{1-\dfrac 1 2^{20+1}}{1-\dfrac 1 2}\). Soit \(\text S=-2\times \left(1-\dfrac 1{2^{21}}\right)\)

T= \(\sum _{\text i=0}^{\text i=20}(v_{\text i}+6\text i)\) = \(\sum _{\text i=0}^{\text i=20}v_{\text i}\) + \(6\times \sum_{\text i=0}^{\text i=20}\text i\) = \(\text S+6\times \dfrac{20\times (20+1)} 2\) = \(1260-2\times \left(1-\dfrac 1{2^{21}}\right)\)

Exercice 8

Soit \(f\)  la fonction définie par \(f(x)=\frac{x-2}{2x^2-5x+4}\) .

  1. Déterminer \(\text D\) , l'ensemble de définition de \(f\) .

  2. Étudier les variations de \(f\)  et dresser son tableau de variation en y indiquant les valeurs extrêmes.

  1. \(2x^2-5x+4\)  est un trinôme du second degré, calculons son discriminant \(\Delta\):

    \(\Delta=25-32=-7\) Ce discriminant étant négatif, le dénominateur de \(f\)  ne s'annule pas et donc \(\text D=\mathbb{R}\) .

  2. \(f\)  est dérivable sur \(\mathbb{R}\) car fonction rationnelle et \(\text D=\mathbb{R}\) .

    f est de la forme \(\dfrac u v\)  avec   \(u(x)=x-2\) , \(u'(x)=1\) , \(v(x)=2x^2-5x+4\) ,  \(v'(x)=4x-5\)

    D'où:

    \(f'(x)=\dfrac{2x^2-5x+4-(x-2)(4x-5)}{(2x^2-5x+4)^2}=\dfrac{-2x^2+8x-6}{(2x^2-5x+4)^2}=\dfrac{-2(x^2-4x+3)}{(2x^2-5x+4)^2}\)

    Or \(x^2-4x+3=(x-1)(x-3)\) .

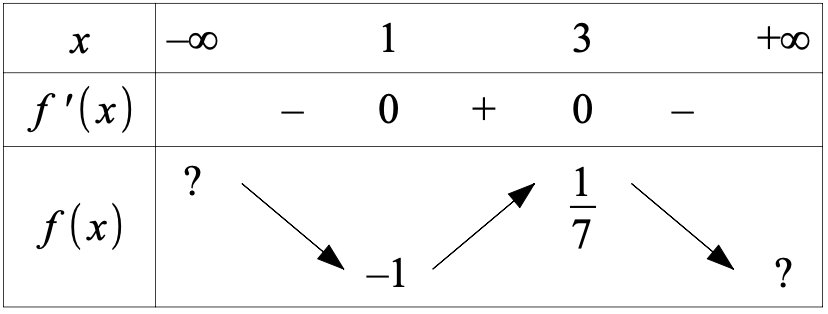
    On obtient le tableau de signe:

    Et celui de variations: