Devoir sur les probabilités 14-15
L'usage de la calculatrice est autorisé.
Durée : 55 min
Exercice 1
On lance deux dés équilibrés dont les faces sont numérotées de 1 à 6.
L'ensemble \(\text E\) des couples \((x\mathrm ;y)\) , avec \(x\) \({\in}\) { 1 ; 2 ; 3 ; 4 ; 5 ; 6 } et \(y\) \({\in}\) { 1 ; 2 ; 3 ; 4 ; 5 ; 6 }, est muni de la loi équirépartie . (c'est à dire toutes les issues sont équiprobables)
À chaque couple \((x\mathrm ;y)\) , ont associe \(\left|x-y\right|\).
On définit ainsi une variable aléatoire \(\text X\) sur l'ensemble \(\text E\) .
-
Définir la loi de probabilité de \(\text X\).
-
Calculer l'espérance et la variance de \(\text X\).
| \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | |
|---|---|---|---|---|---|---|
| \(1\) | 0 | 1 | 2 | 3 | 4 | 5 |
| \(2\) | 1 | 0 | 1 | 2 | 3 | 4 |
| \(3\) | 2 | 1 | 0 | 1 | 2 | 3 |
| \(4\) | 3 | 2 | 1 | 0 | 1 | 2 |
| \(5\) | 4 | 3 | 2 | 1 | 0 | 1 |
| \(6\) | 5 | 4 | 3 | 2 | 1 | 0 |
D'où la loi de probabilité
| \(x_i\) | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
|---|---|---|---|---|---|---|
| \(p(\text X=x_i)\) | \(\dfrac 6{36}\) | \(\dfrac{10}{36}\) | \(\dfrac 8{36}\) | \(\dfrac 6{36}\) | \(\dfrac 4{36}\) | \(\dfrac 2{36}\) |
\(\text E(\text X)=\frac{10+16+18+16+10}{36}=\frac{35}{18}\)
\(\text V(\text X)=\frac{10}{36}+\frac{4\times 8}{36}+\frac{9\times 6}{36}+\frac{16\times 4}{36}+\frac{25\times2}{36}-\text E(\text X)^2=\frac{10+32+54+64+50}{36}-\text E(\text X)^2=\frac{665}{324}\)
Exercice 2
On dispose de deux dés cubiques non truqués.
L'un a cinq faces rouges et une face verte, l'autre a une face rouge, deux vertes et trois bleues.
On jette les deux dés :
-
on gagne 5 euros si les deux faces obtenues sont rouges;
-
on gagne 2 euros si les deux faces obtenues sont vertes;
-
on perd 1 euro si les deux faces obtenues sont de couleurs différentes.
On appelle \(\text X\) la variable aléatoire égale au gain ou à la perte ainsi réalisés.
-
Déterminer la loi de probabilité de \(\text X\).
-
Déterminer l'espérance, la variance et l'écart type de \(\text X\).
-
On commence par dessiner un arbre pour mieux raisonner ensuite:
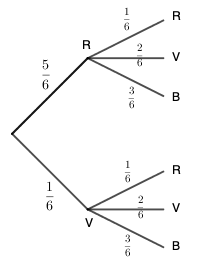
\(\text P(\text{Rouge})=\frac 5 6\times \frac 1 6=\frac 5{36}\) et \(\text P(\text{Vert})=\frac 16\times \frac 2 6=\frac 2{36}\)
Comme le premier dé n'a que deux couleurs, on a ici tous les cas pour des couleurs identiques.
D'où \(\text P(\text{Différent})=1-\left(\frac 5{36}+\frac 2{36}\right)\)
On obtient la loi de probabilité :
\(x_i\) \(-1\) \(2\) \(5\) \(\text P(\text X=x_i)\) \(\frac{29}{36}\) \(\frac 2{36}\) \(\frac 5{36}\) -
Espérance, variance et écart type.
Exercice 3
Une variable aléatoire \(\text X\) suit la loi de probabilité suivante :
| \(x_i\) | \(-3\) | \(1\) | \(2\) | \(5\) |
|---|---|---|---|---|
| \(\text{P}(\text{X}=x_i)\) | \(0,1\) | \(p\) | \(q\) | \(0,3\) |
Déterminer les valeurs des réels \(p\) et \(q\) tels que \(\text E(\text X)=2\) et \(\text V(\text X)=5,6\).
\(\text E(\text X)=2 \Leftrightarrow -0,3+p+2q+1,5=2\) \(\Leftrightarrow\) \(p+2q=0,8\) et \(0,4+p+q=1\) soit \(p+q=0,6\)
On obtient donc le système : \(\left\{\begin{matrix}p+2q=0,8\\\\p+q=0,6\end{matrix}\right.\) qui après résolution donne \(p=0,4\) et \(q=0,2\) .
\(V(X)=5,6 \Leftrightarrow 0,9+p+4q+7,5-\text E(\text X)^2=5,6\) \(\Leftrightarrow\) \(p+4q=1,2\).
Les solutions trouvées précédemment conviennent donc on a pour couple solution \((p\mathrm ;q)=(0,4\mathrm ;0,2)\) .
Exercice 4
Prouver que \(\text E(a\text X+b)=a\text E(\text X)+b\).