Devoir Dérivation
L’usage de la calculatrice est autorisé
Un soin particulier sera apporté à la rédaction et aux justifications.
Durée : 55 min
Exercice 1 (2,5 points)
\(\text{C}_f\) est la fonction définie sur \(\mathbb{R}^*\) par \(f(x)=x-\dfrac{1}{x}\).
-
Vérifiez que pour tout \(h \ne 0\) et \(1+h>0\) :
\[f(1+h)=\dfrac{2h+h^2}{1+h}\] -
Déduisez-en que \(f\) est dérivable en \(1\) et calculez \(f'(1)\).
Exercice 2 (2,5 points)
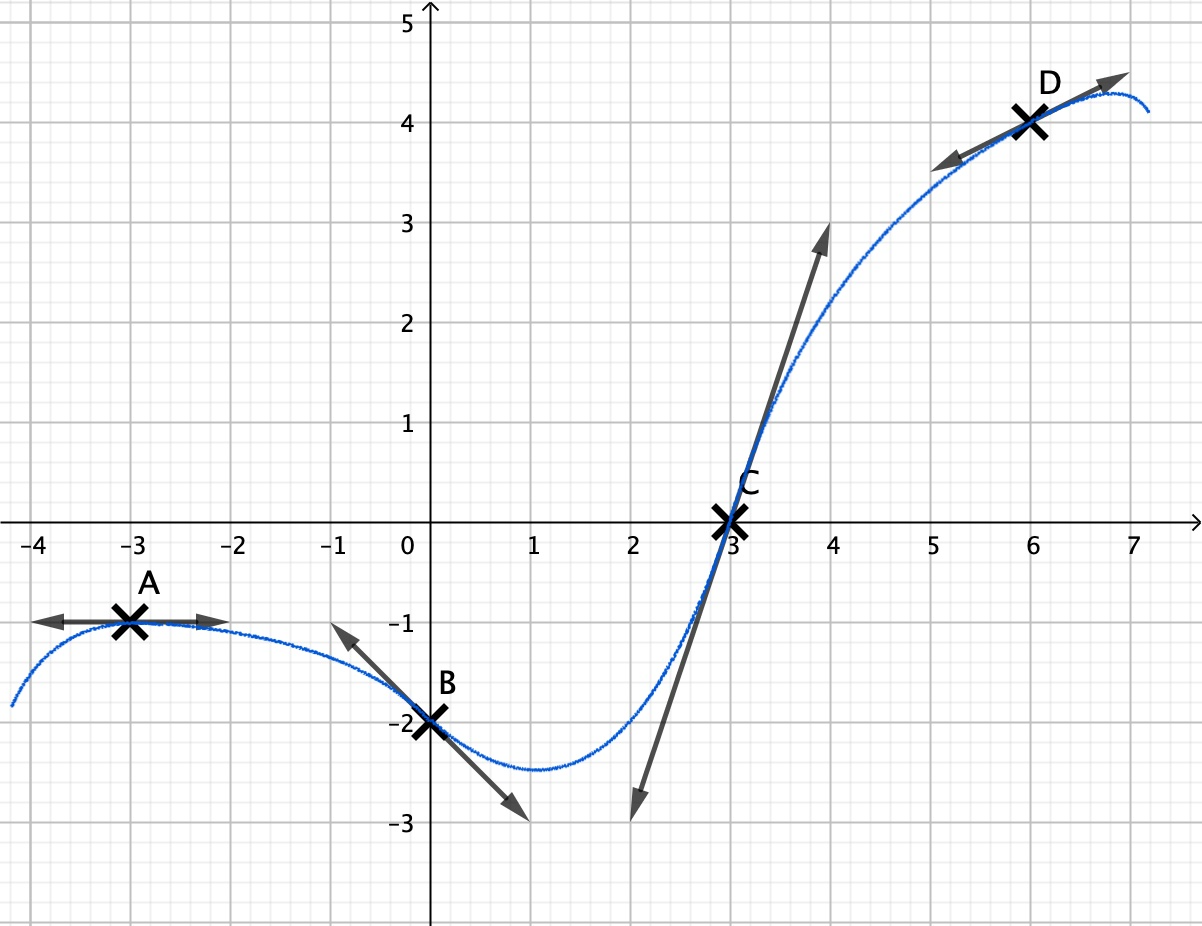
\(\text{C}_f\) est la courbe représentative d’une fonction \(f\) définie et dérivable sur \(\mathbb{R}\).
On donne:
\(f(-3)=-1\) \(f(-0)=-2\) \(f(3)=0\) \(f(6)=4\)
\(f'(-3)=0\) \(f'(0)=-1\) \(f'(3)=3\) \(f'(6)=0.5\)
- Placez les points \(\text{A}\), \(\text{B}\), \(\text{C}\) et \(\text{D}\) d’abscisses respectives \(-3\); \(0\); \(3\) et \(6\).
- Construisez les tangentes à \(\text{C}_f\) aux points \(\text{A}\), \(\text{B}\), \(\text{C}\) et \(\text{D}\).
- Dessinez une allure possible de la courbe sur l’intervalle \([-3;6]\).
Exercice 3 (4,5 points)
\(f\) est une fonction et \(a\) un nombre donné. \(f\) est dérivable en \(a\). Déterminez une équation de la tangente à la courbe représentative de \(f\) au point d’abscisse \(a\).
-
\(f(x)=3x^3+5x-2\) et \(a=-2\).
-
\(f(x)=(2x+1)^{10}\) et \(a=0\).
-
\(f(x)=(4x+8)\sqrt{x}\) et \(a=4\).
Exercice 4 (2,5 points)
\(f\) est la fonction définie sur \(\mathbb{R}-\{-1\}\) par \(f(x)=\dfrac{2x}{x+1}\), et \(\text{C}_f\) est sa courbe représentative.
-
Calculez \(f'(x)\).
-
Quels sont les points de \(\text{C}_f\) en lesquels la tangente à \(\text{C}_f\) est parallèle à la droite d’équation \(y=4x\)?
Exercice 5 (3 points)
La figure ci-dessous représente un écran de jeu vidéo. Un avion remonte l’écran de gauche à droite en suivant la courbe d’équation . L’avion peut tirer des missiles selon la tangente à sa trajectoire.
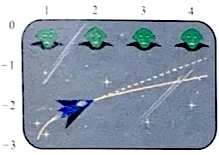
En quels points de sa trajectoire l’avion doit-il tirer ses missiles pour abattre successivement les quatre monstres situés en haut de l’écran en \((1;0)\), \((2;0)\), \((3;0)\) et \((4;0)\) ?
Exercice 1
-
On a \(f(1+h)=1+h-\dfrac 1{1+h}=\dfrac{(1+h)^2-1}{1+h}=\dfrac{2h+h^2}{1+h}\)
-
On calcule \(\text T_{f,1}=\dfrac{f(1+h)-f(1)} h=\dfrac{f(1+h)} h=\dfrac{2+h}{1+h}\) or \(\lim \limits_{h\rightarrow 0}\text T_{f,1}=2\) .
On a donc \(f\) dérivable en 1 et \(f'(1)=2\) .
Exercice 2
Un exemple de solution est donné ci-dessous, il est important que la courbe passe par les points A,B,C et D, en suivant localement la tangente en ces points.
Exercice 3
-
On a \(f(-2)=-36\) .
La fonction est polynomiale donc dérivable en -2, on a \(f'(x)=9x^2+5\) .
D'où \(f'(-2)=41\) .
Une équation de la tangente à \(\text C_f\) en \(-2\) s'écrit alors :
\(y=f'(-2)(x+2)+f(-2)=41x+46\) .
-
On a \(f(0)=1\) .
\(f\) est une fonction polynomiale, donc dérivable en 0. \(f\) de la forme \(g(\mathit{ax}+b)\) avec \(g(x)=x^{10}\) . D'où \(f'(x)=2\times 10\times (2x+1)^9=20(2x+1)^9\) et \(f'(0)=20\) .
Une équation de la tangente à \(\text C_f\) en \(0\) s'écrit alors : \(y=f'(-2)(x+2)+f(-2)=41x+46\) .
-
On a \(f(4)=48\) .
\(f\) est un produit de fonctions dérivables en 4, donc est une fonction dérivable en 4.
On a \(f=u\times v\) avec \(u(x)=4x+8\) et \(v(x)=\sqrt x\) soit \(u'(x)=4\) et \(v'(x)=\dfrac 1{2\sqrt x}\) .
Sur \(]0\mathrm ;+\infty [\) , on a donc \(f'(x)=u'(x)v(x)+u(x)v'(x)\)
\(\Rightarrow\) \(f'(x)=4\sqrt x+\dfrac{2x+4}{\sqrt x}\)
\(\Rightarrow\) \(f'(4)=8+6=14\)
Une équation de la tangente à \(\text C_f\) en \(4\) s'écrit alors : \(y=f'(4)(x-4)+f(4)=14x-8\) .
Exercice 4
-
\(f\) est une fonction rationnelle, donc dérivable sur son ensemble de définition. \(f\) est de la forme \(\dfrac u v\) , avec \(u(x)=2x\) et \(v(x)=x+1\) soit \(u'(x)=2\) et \(v'(x)=1\) .
Sur \(\mathbb{R}\)-{-1}, on a \(f'(x)=\dfrac{u'(x)v(x)-u(x)v'(x)}{v^2(x)}\) .
\(\Rightarrow\) \(f'(x)=\dfrac{2(x+1)-2x\times 1}{(x+1)^2}\).
\(\Rightarrow\) \(f'(x)=\dfrac 2{(x+1)^2}\).
-
Si la tangente est parallèle à la droite d'équation \(y=4x\) , alors on a \(f'(x)=4\) .
On résout cette équation : \(f'(x)=4\) \(\Leftrightarrow\) \(\dfrac 2{(x+1)^2}=4\) \(\Leftrightarrow\) \((x+1)^2=\dfrac 1 2\) \(\Leftrightarrow\) \((x+1)^2-\left(\dfrac{\sqrt 2} 2\right)^2=0\)
\(\Leftrightarrow \left(x+1-\dfrac{\sqrt 2} 2\right)\left(x+1+\dfrac{\sqrt 2} 2\right)=0\).
La tangente est donc parallèle à la droite d'équation \(y=4x\) aux points A et B de \(\text C\) d'abscisses respectives \(-1+\dfrac{\sqrt 2} 2\) et \(-1-\dfrac{\sqrt 2} 2\) .
Soit \(\text A\left(-1+\dfrac{\sqrt 2} 2\mathrm ;-2\sqrt 2+2\right)\) et \(\text B\left(-1-\dfrac{\sqrt 2} 2\mathrm;2\sqrt 2+2\right)\)
Exercice 5
Soit \(f(x)=-1-\dfrac 1 x\) et \(f'(x)=\dfrac 1{x^2}\) .
Une équation de la tangente à la courbe représentative de \(f\) s'écrit alors :
Supposons que le point \(\text B(b,0)\) appartienne à cette tangente, on a donc:
\(\dfrac 1{a^2}b-1-\dfrac 2 a=0\) \(\Leftrightarrow\) \(-a^2-2a+b=0 \Leftrightarrow\) \(a^2+2a-b=0 \Leftrightarrow\) \((a+1)^2-(1+b)=0\)
D'après l'énoncé, on a \(b>0\) , donc \(1+b>0\) .
On peut alors écrire : \((a+1)^2-(\sqrt{1+b})^2=0\) d'où \(a+1=\sqrt{1+b}\) et \(a=\sqrt{1+b}-1\) ou \(a+1=-\sqrt{1+b}\) et \(a=-\sqrt{1+b}-1\) or \(a>0\) (On se situe sur une partie du plan où \(x>0\)), donc la seule solution possible est \(a=\sqrt{1+b}-1\).
Reste à conclure (les ordonnées peuvent être récrites):
Pour \((1\mathrm ;0)\) on obtient \(a=\sqrt 2-1\) , un tir au point \(\left(\sqrt 2-1\mathrm ;-1-\dfrac 1{\sqrt 2-1}\right)\) permettra donc de se débarrasser du premier monstre.
Pour \((2\mathrm ;0)\) on obtient \(a=\sqrt 3-1\) , un tir au point \(\left(\sqrt 3-1\mathrm ;-1-\dfrac 1{\sqrt 3-1}\right)\) permettra donc de se débarrasser du second monstre.
Pour \((3\mathrm ;0)\) on obtient \(a=\sqrt 4-1=1\) , un tir au point \((1\mathrm ;-2)\) permettra donc de se débarrasser du troisième monstre.
Pour \((4\mathrm ;0)\) on obtient \(a=\sqrt 5-1\) , un tir au point \(\left(\sqrt 5-1\mathrm ;-1-\dfrac 1{\sqrt 5-1}\right)\) permettra donc de se débarrasser du quatrième monstre.