Devoir Nombre dérivé
L'usage de la calculatrice n'est pas autorisé.
Barème donné à titre totalement indicatif
Durée: 55min
Exercice 1
Soit \(f\) la fonction définie sur \(\left[\dfrac{3}{2};+\infty\right[\) par \(f(x)=\sqrt{2x-3}\).
-
Calculer le taux d’accroissement de \(f\) en \(4\).
-
En déduire le nombre dérivé de \(f\) en 4.( 1,5 pts)
Exercice 2
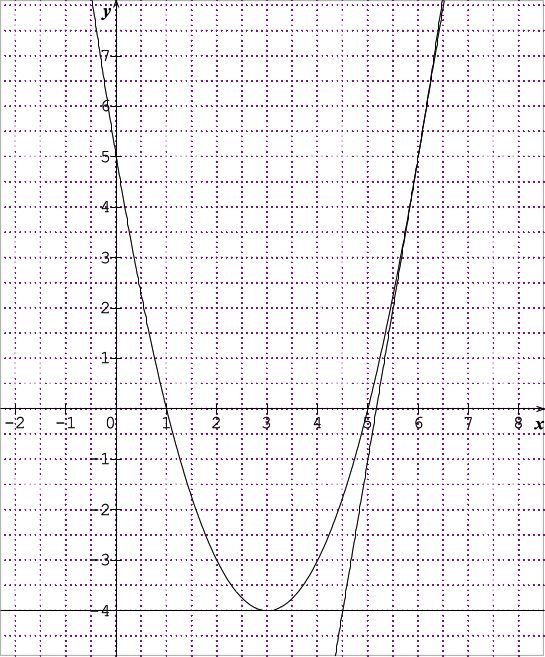
On a représenté ci-dessous la courbe représentative de la fonction \(f\) et tracé deux tangentes à la courbe aux points \(\text{A}(3;f(3))\) et \(\text{B}(6;f(6))\) .
-
Lire le nombre dérivé de \(f(x)\) en 3.( 0,25 pt)
-
Lire \(f'(6)\). ( 0,25 pt)
-
En déduire une équation sous forme réduite de la tangente à \(\text{C}_f\) au point \(\text{B}\). ( 1 pt)
Exercice 3 :
Soit \(f\) la fonction définie sur \(\mathbb{R}\) par \(f(x)=\dfrac{1}{4}x^4-2x^2+3\)
On appelle \(\text{C}_f\) sa courbe représentative dans un repère orthonormal.
- Déterminer une équation de la tangente à \(\text{C}_f\) au point d’abscisse \(1\). ( 1 pt)
- Démontrer que, pour tout réel \(x\), \(\dfrac{1}{4}x^4-2x^2+3x-\dfrac{5}{4}=\dfrac{1}{4}(x-1)^2(x^2+2x-5)\) ( 1 pt)
- Etudier la position relative (dessus-dessous!) de la tangente \(\text{T}\) à \(\text{C}_f\) au point d’abscisse \(1\) par rapport à la courbe représentative de \(f\). ( 2 pts)
Exercice 4 :
\((\text{C}_f)\) et \((\text{C}_g)\) sont les courbes représentant respectivement les fonctions \(f\) et \(g\) définies sur \(\mathbb{R}\) par \(f(x)=0.5x^2+x+0.5\) et \(g(x)=-(x-2)^2+3\).
- Etudier les variations de \(f\) et \(g\). ( 1 pt)
- Montrer que \(\text{A}(1;2)\) est commun à \((\text{C}_f)\) et \((\text{C}_g)\). ( 0,5 pt)
- Montrer que les deux courbes admettent en \(\text{A}\) une même tangente \(\text{T}\). ( 1,25 pts)
- La droite d’équation \(y=\dfrac{1}{5}x+\dfrac{9}{50}\) est-elle tangente à la courbe \((\text{C}_f)\) ? Justifier. (1,5 pts)
Exercice 1
-
On calcule \(\text T_{f,4}=\dfrac{f(4+h)-f(4)} h=\dfrac{\sqrt{8+2h-3}-\sqrt 5} h=\dfrac{\sqrt{5+2h}-\sqrt 5} h=\dfrac 2{\sqrt{5+2h}+\sqrt 5}\)
-
On a \(\lim \limits_{h\rightarrow 0}\text T_{f,4}=\dfrac 1{\sqrt 5}\) donc \(f'(4)=\dfrac 1{\sqrt 5}\)
Exercice 2
-
\(f'(3)=0\)
-
\(f'(6)=6\)
-
\(f(6)=5\) d'où \(y=f'(6)(x-6)+f(6)\) est l'équation de la tangente à \(\text C_f\) en \(\text B\) .
\(\Rightarrow\) \(y=6(x-6)+5\) \(\Rightarrow\) \(y=6x-31\) sous forme réduite.
Exercice 3
-
On calcule \(\text T_{f,1}=\dfrac{f(1+h)-f(1)} h\)
On calcule préalablement:
\((1+h)^2=1+2h+h^2\)
et
\(((1+h)^2)^2=(1+2h+h^2)^2=1+4h+4h^2+h^2+h^2+4h^3+h^4=1+4h+6h^2+4h^3+h^4\)
\(f(1)=\dfrac 1 4-2+3=\dfrac 5 4\) et \(f(1+h)=\dfrac 1 4(1+4h+6h^2+4h^3+h^4)-2(1+2h+h^2)+3\)
D'où \(f(1+h)=\dfrac 5 4-3h-\dfrac 1 2h^2+h^3+\dfrac 1 4h^4\)
Soit \(\text T_{f,1}=-3-\dfrac 1 2h+h^2+\dfrac 1 4h^3\) et \(\lim \limits_{h\rightarrow 0}\text T_{f,1}=-3\) \(\Rightarrow\) \(f'(1)=-3\)
D'où l'équation réduite de la tangente à \(\text C_f\) en 1:
\(y=-3(x-1)+f(1)=-3x+3+\dfrac 5 4=-3x+\dfrac{17} 4\)
-
\((x-1)^2(x^2+2x-5)=(x^2-2x+1)(x^2+2x-5)=x^4-4x^2-5x^2+x^2+10x+2x-5\) \((x-1)^2(x^2+2x-5)=x^4-8x^2+12x-5\) d'où \(\dfrac 1 4(x-1)^2(x^2+2x-5)=\dfrac 1 4x^4-2x^2+3x-\dfrac 5 4\) .
-
On étudie le signe de \(f(x)-\left(-3x+\dfrac{17} 4\right)=f(x)+3x-\dfrac{17} 4=\dfrac 1 4x^4-2x^2+3x-\dfrac 5 4\)
D'où \(f(x)-\left(-3x+\dfrac{17} 4\right)=\dfrac 1 4(x-1)^2(x^2+2x-5)\).
On cherche le signe de cette quantité, on a \(\dfrac 1 4(x-1)^2\geqslant 0\) , le signe de \(f(x)-\left(-3x+\dfrac{17} 4\right)\) est donc celui de \(x^2+2x-5\) . C'est un trinôme du second degré avec \(\Delta=4+20=24\) soit:
\(x_1=\dfrac{-2-\sqrt{24}} 2=-1-\sqrt 6\) et \(x_2=\dfrac{-2+\sqrt{24}} 2=-1+\sqrt 6\) .
On a, de plus \(a>0\) \((a=1)\) . D'où \(f(x)-\left(-3x+\dfrac{17} 4\right)\) négatif sur \([-1-\sqrt 6,-1+\sqrt 6]\) , et positif ailleurs.
Sur l'intervalle \([-1-\sqrt 6,-1+\sqrt 6]\) la tangente T au point d'abscisse 1 est donc en dessous de \(\text C_f\) (points de contact aux points d'abscisses \(-1-\sqrt 6\) , \(-1+\sqrt 6\) et 1) et au dessus sur l'union d'intervalles \(]-\infty \mathrm ;-1-\sqrt 6]{\cup}[-1+\sqrt 6,+\infty [\) .
Exercice 4
-
\(f(x)=\dfrac 1 2(x+1)^2\) et \(g(x)=-(x-2)^2+3\) , ce sont des formes canoniques, on déduit:

-
\(f(1)=\dfrac 1 2(1+1)^2=2\) et \(g(1)=-(1-2)^2+3=2\) \(\Rightarrow\) le point \(\text A(1\mathrm ;2)\) est bien commun à \(\text C_1\) et \(\text C_2\) .
-
Soit une fonction du second degré: \(k\) : \(x \mapsto ax^2+bx+c\) , cherchons son nombre dérivé en \(x_0\) :
\(\text T_{k,x_0}=\dfrac{a(x_0+h)^2+b(x_0+h)+c-(ax_0^2+\mathit{bx}_0+c)} h\)
\(\Rightarrow \text T_{k,x_0}=\dfrac{ax_0^2+2\mathit{ahx}_0+\mathit{ah}^2+\mathit{bx}_0+\mathit{bh}+c-ax_0^2-\mathit{bx}_0-c} h\)
\(\Rightarrow\) \(\text T_{k,x_0}=\dfrac{2\mathit{ahx}_0+\mathit{ah}^2+\mathit{bh}} h\)
\(\Rightarrow\) \(\text T_{k,x_0}=2\mathit{ax}_0+\mathit{ah}+b\)
or \(\lim \limits_{h\rightarrow 0}\text T_{k,x_0}=2\mathit{ax}_0+b\) donc \(k'(x_0)=2\mathit{ax}_0+b\) .
On a donc \(f'(1)=2\times \dfrac 1 2\times 1+1=2\) et \(g(x)=-x^2+4x-1\) soit \(g'(1)=-2\times 1+4=2\)
Les courbes \((\text C_1)\) et \((\text C_2)\) admettent donc une même tangente T en 1.
-
On cherche \(a\) tel que \(f(a)=\dfrac 1 5a+\dfrac 9{50}\) et \(f'(a)=\dfrac 1 5\)
\(f'(a)=\dfrac 1 5\) \(\Rightarrow\) \(f'(a)=a+1=\dfrac 1 5\) \(\Rightarrow\) \(a=-\dfrac 4 5\)
On a \(f\left(-\dfrac 4 5\right)=\dfrac 1 2\left(-\dfrac 4 5\right)^2-\dfrac 4 5+\dfrac 1 2=\dfrac 8{25}-\dfrac{20}{25}+\dfrac 1 2=-\dfrac{24}{50}+\dfrac{25}{50}=\dfrac 1{50}\)
et
\(\dfrac 1 5-\dfrac 4 5+\dfrac 9{50}=-\dfrac 8{50}+\dfrac 9{50}=\dfrac 1{50}\)
D'où \((\text C_1)\) et la droite d'équation \(y=\dfrac 1 5x+\dfrac 9{50}\) sont bien tangentes au point de coordonnées \(\left(-\dfrac 4 5\mathrm ;\dfrac 1{50}\right)\) .