Devoir Nombre dérivé

L'usage de la calculatrice est autorisé.

Durée: 30min

Exercice 1

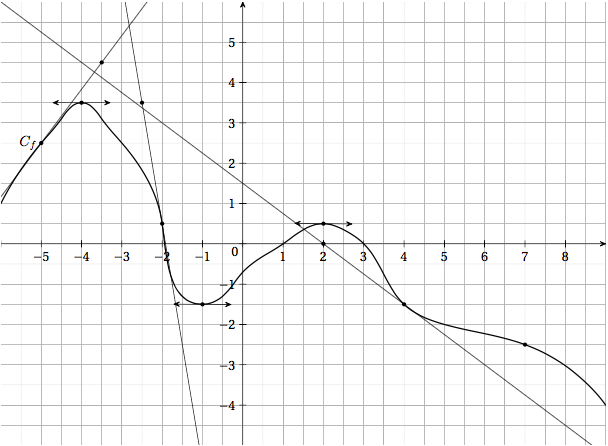
Voici la courbe représentative \(\text{C}_f\) d'une fonction \(f\) définie sur \(\mathbb{R}\)

1. D'après le graphique, donner la valeur de: \(f'(-5)\), \(f'(-4)\), \(f'(-2)\) et \(f'(4)\).

2. Donner l'équation de la tangente à \(\text{C}_f\) au point d'abscisse \(4\) et celle au point d'abscisse \(-2\).

Exercice 2

Soit \(f\) une fonction définie et dérivable sur \(\mathbb{R}\), et soit \(\text{C}_f\) sa courbe représentative dans un repère.

On sait que les points \(\text{A}(-2;1)\), \(\text{B}(0;3)\) et \(\text{C}(3;-1)\) appartient à \(\text{C}_f\).

On sait de plus que \(f'(-2)=\dfrac{3}{2}\), \(f'(0)=0\) et \(f'(3)=-2\)

Dessiner une courbe \(\text{C}_f\) vérifiant toutes ces conditions.

Exercice 3

Soit \(f\) une fonction définie sur \([0;2]\) par :

\[\left \{ \begin{array}{rcl} x^2+1 \text{ si } x \leqslant 1\\ -x^2+4x-1 \text{ si } x>1 \end{array} \right.\]

\(f\) est-elle dérivable en \(1\) ? Si oui, quel est alors son nombre dérivé en \(1\)?