Aller au contenu

Devoir sur les fonctions dérivées 18-19

Dérivation pour milieux autorisés

L'usage de la calculatrice est autorisé, notamment pour multiplier par deux.

Les détails de calculs sont attendus et exigés.

Vous pouvez faire les exercices dans l'ordre souhaité.

Faîtes des phrases simples (sujet-verbe-compléments) afin d'être bien compris..

La clarté de la rédaction est prise en compte dans la notation.

Exercice 1

Soit \(f\)  la fonction définie sur \(\mathbb{R}\) par :

\[f(x)=-x^3-2x^2+4x+3\]

  1. a. Déterminer \(f'(x)\)  sur \(\mathbb{R}\).

    b. En déduire le tableau de variation de la fonction \(f\)  sur \(\mathbb{R}\). Calculer les extrema à la calculatrice (valeurs exactes).

  2. a. À l'aide de la calculatrice, visualiser la courbe représentative de \(f\)  et conjecturer une racine \(x_1\) simple de ce polynôme du troisième degré.

    b. Vérifiez votre conjecture par le calcul.

  3. Déterminer les trois coefficients \(a\) , \(b\)  et \(c\)  tels que, pour tout \(x\)  de \(\mathbb{R}\), on ait : \(f(x)=(x-x_1)(ax^2+bx+c)\) .

    Expliquer clairement la démarche.

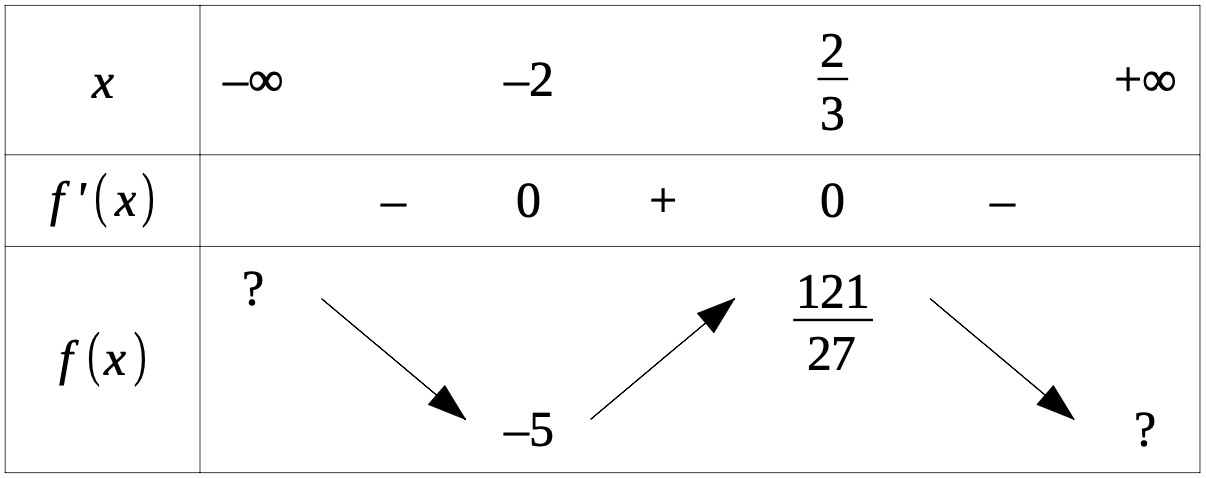
  1. a. \(f'(x)=-3x^2-4x+4\)  sur \(\mathbb{R}\) comme toute fonction polynomiale qui se respecte.

    b. \(\Delta =16+3\times 4\times 4=16\times 4=64=8^2\)  donc \(\Delta >0\)  soit deux racines distinctes :

    \(x_1=\dfrac{4+8}{-6}=\dfrac{12}{-6}=-2\)  et \(x_2=\dfrac{4-8}{-6}=\dfrac{-4}{-6}=\dfrac 2 3\) .

    Comme \(a=-3\)  et \(a<0\) , la parabole représentative de \(f'\) a des branches qui partent vers le bas. \(f'(x)\) est donc négative à l'extérieur des racines et positive à l'intérieur.

    De plus, \(f(-2)=-5\)  et \(f\left(\dfrac 2 3\right)=\dfrac{121}{27}\) pour les extrema locaux à la calculatrice.

  2. a. On conjecture que \(f(-3)=0\)  car la courbe \(\text C_f\)  coupe l'axe \((\text Ox)\)  pour \(x\approx -3\) . \(x_1=-3\)  serait donc une racine entière de ce polynôme du troisième degré.

    b. \(f(-3)=-(-3)^3-2(-3)^2-12+3=27-18-9=27-27=0\)  ce qui montre que \(x_1=-3\)  est effectivement une racine de ce polynôme ce qui donne le droit d'écrire la relation suivante :

    \(f(x)=(x+3)(ax^2+bx+c)\)  avec \(a\) , \(b\)  et \(c\)  trois nombres réels.

  3. On développe l'expression afin de comparer les écritures développées:

    \(f(x)=ax^3+bx^2+3ax^2+3bx+cx+3c=-x^3-2x^2+4x+3\).

    Par identification, on a avec le terme en \(x^3\)  l'égalité \(a=-1\) .

    Par identification, on a avec le terme constant l'égalité \(3c=3\) soit \(c=1\) .

    Par identification, on a avec le terme en \(x^2\)  l'égalité \(b+3a=-2\) soit \(b-3=-2\)  soit \(b=1\).

    Avec ces trois valeurs, on retrouve bien le terme en \(x\)  qui vaut \(3b+c=3+1=4\) .

    Finalement, \(f(x)=(x+3)(-x^2+x+1)\) .

    Remarque: cette méthode d'identification est absolument à éviter dans des filières post-bac exigeantes, car elle nécessite d'avoir au préalable démontré l'unicité de l'écriture d'un polynôme.

Exercice 2

On veut construire une cuve métallique, ayant la plus grande capacité possible, à partir d'une plaque carrée donnée de \(3\) m de côté.

  • L'unité est le mètre.

  • Vous donnerez les valeurs exactes puis arrondirez au mm près lorsque ce sera nécessaire.

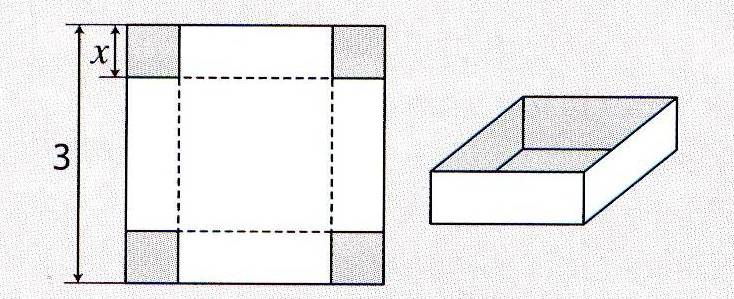
À chaque coin ce cette plaque, on découpe un carré de côté \(x\) m. En pliant et en soudant, on obtient une cuve de volume \(V(x)\) .

  1. a. Montrer que l'ensemble de définition de \(V\)  est \([0;1,5]\) .

    b. Démontrer que le volume de la cuve s'écrit :

    \[V(x)=4x^3-12x^2+9x\]

  2. a. Étudier les variations de la fonction \(V\)  et établir le tableau de variations de  \(V\).

    b. Décrire précisément la cuve qui répond le mieux au problème de départ.

    c. Quel est le pourcentage de matériau non utilisé par plaque ?

  1. a. Il faut que \(x\geqslant 0\)  car c'est une longueur. De plus, le coté  \(c\)  du carré intérieur est tel que \(c=3-2x\)  et \(c\geqslant 0\)  ce qui donne \(3-2x\geqslant 0\)  soit \(3\geqslant 2x\) soit \(\dfrac 3 2\geqslant x\) .

    Finalement, \(0\leqslant x\leqslant \dfrac 3 2\)  soit \(\text D_{V}=\left[0 ;\dfrac 3 2\right]\).

    b. \(V(x)=c\times c\times h=x(3-2x)^2=x(9-12x+4x^2)=4x³-12x^2+9x\) .

  2. a. \(V\) est dérivable sur \(\mathbb{R}\) donc sur \(\text D_{V}=\left[0;\dfrac 3 2\right]\)  telle que \(V'(x)=12x^2-24x+9\) . Avec le facteur \(3\), on a \(V'(x)=3(4x^2-8x+3)\)  soit un trinôme simple !

    \(\Delta =64-4\times 3\times 4=64-48=16=4^2\)  Soit \(\Delta >0\)  soit

    deux racines distinctes :

    \(x_1=\dfrac{8+4} 8=\dfrac{12} 8=\dfrac 3 2\)  qui est hors de \(\text D_{V}\)  et \(x_2=\dfrac{8-4} 8=\dfrac 4 8=\dfrac 1 2=0,5\)  qui est dans \(\text D_{V}\) .

    De plus \(a=4\)  soit \(a>0\)  donc la parabole est orientée vers le bas, ce qui donne le tableau :

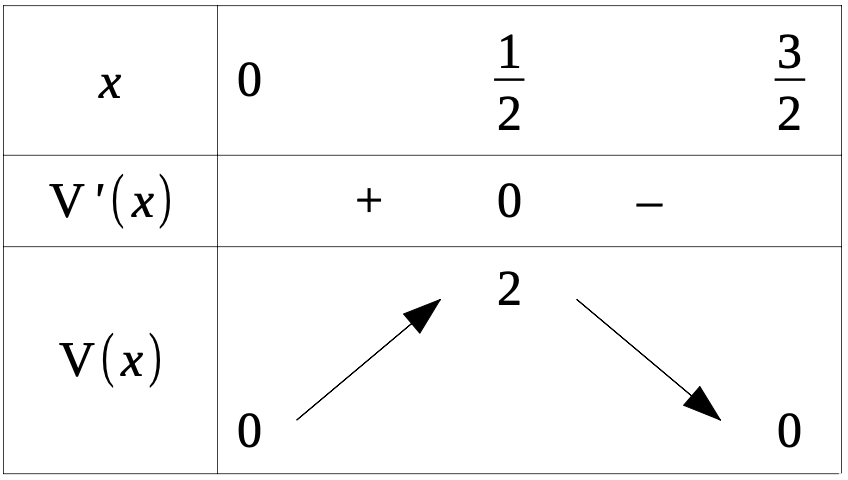
    b. On obtient la meilleure cuve avec \(x=0,5 \, m\) et elle a alors une capacité de \(2\,\text{m}^3\).

    c. On calcule le rapport : \(\dfrac{4x^2}{3^2}=\dfrac 1 9\)  avec \(x=\dfrac 1 2\)  soit \(11,1\)  % de matériau non utilisé.

Exercice 3

\(\text{ABCD}\)  est un carré de côté \(1\) dm. \(\text C\)  est le quart de cercle de centre \(\text A\)  et de rayon \(\text{AB}\)  contenu dans le carré. \(T\)  est un point de \(\text C\)  distinct de \(\text B\)  et de \(\text D\) . La tangente \((d)\) en \(\text T\) coupe \([\text{DC}]\)  en \(\text M\)  et coupe \([\text{BC}]\)  en \(\text N\).

On note : \(x=\text{DM}\)  et \(y=\text{BN}\) .

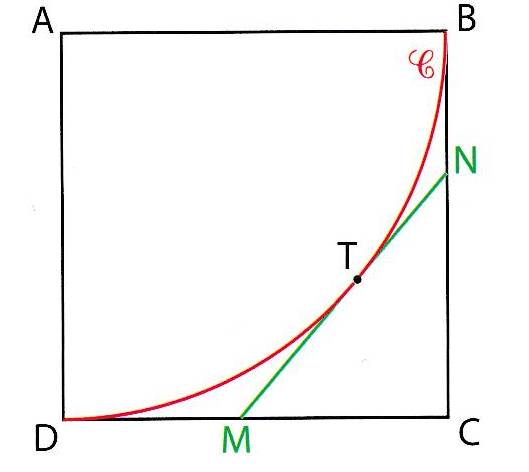
Partie A

  1. Démontrer que \(\text{MN}^2=x^2+y^2-2x-2y+2\)

  2. Montrer que \(\text{MN}=\text{MT}+\text{TN}=x+y\) .

    On pourra tracer \(\text{[AT]}\)  et \(\text{[AN]}\)  pour s'aider.

  3. À l'aide des deux questions précédentes, en déduire l'expression de \(y\)  en fonction de \(x\) .

  4. Exprimer la longueur \(\text{MN}\)  en fonction de \(x\) .

Partie B

Soit la fonction \(f\)  définie par \(f(x)=\dfrac{x^2+1}{x+1}\)  sur \([0;1]\) .

  1. Déterminer \(f'(x)\).

  2. Étudier les variations de \(f\)  sur \([0;1]\) .

Partie C

  1. Pour quelle position du point \(\text M\) , la longueur \(\text{MN}\) est-elle minimale ? Valeur exacte puis arrondie.

  2. Combien mesure-t-elle ? Valeur exacte puis arrondie.

Bonus (à la demande de Nizar): Déterminer une expression de la fonction \(h\)  dont le quart de cercle de l'exercice \(3\)  est la représentation graphique.

Partie A

  1. On utilise le théorème de Pythagore dans \(\text{MNC}\)  rectangle en \(\text C\) .

    \(\text{MN}^2=(1-x)^2+(1-y)^2=x^2+y^2-2x-2y+2\).

  2. On considère les triangles \(\text{ABN}\)  et \(\text{ATN}\)  tous deux rectangles en \(\text B\)  et en \(\text T\)  car \((\text{MN})\)  est la tangente au cercle en \(\text T\) .

    Avec les deux angles droits, on reconnaît la propriété de la bissectrice \((\text{AT})\)  de l'angle \(\widehat {\text{ABT}}\)  donc \(\widehat{\text{ABN}}=\widehat {\text{NAT}}=\dfrac 1 2\widehat {\text{ABT}}\).

    De plus, ils ont le côté \([\text{AT}]\)  (leur hypoténuse) en commun et ils sont tels que \(\text{AB}=\text{AT}=\text R=1\) dm. Avec ces points communs, les deux triangles sont identiques (avec toutes les mêmes mesures). Donc on a:

    \[\text{MN}=\text{MT}+\text{TN}=x+y\]

  3. On a donc que \(\text{MN}^2=(x+y)^2=x^2+y^2-2x-2y+2\)  soit \(x^2+2xy+y^2=x^2+y^2-2x-2y+2\)  soit \(2xy=-2x-2y+2\)  soit \(2xy+2y=-2x+2\)  soit \(xy+y=-x+1\)  soit \(y(x+1)=-x+1\)  soit \(y=\dfrac{1-x}{1+x}\)  ce qui est possible car \(x \in ]0;1[\) .

  4. \(\text{MN}=x+y=x+\dfrac{1-x}{1+x}=\dfrac{x+x^2+1-x}{1+x}=\dfrac{x^2+1}{x+1}\) et on reconnaît \(f(x)\)  en faisant semblant d'être agréablement surpris...

Partie B

  1. On reconnaît la formule \(\dfrac u v\)  avec \(v\neq 0\)  ce qui donne :

    \(u(x)=x^2+1\)  soit \(u'(x)=2x\)     et     \(v(x)=1+x\) soit \(v'(x)=1\)

    \(f'(x)=\dfrac{2x(1+x)-(x^2+1)}{(x+1)^2}=\dfrac{2x^2+2x-x^2-1}{(1+x)^2}=\dfrac{x^2+2x-1}{(1+x)^2}\).

  2. Le dénominateur est positif car c'est un carré. Le signe est donné par le trinôme : \(\Delta =4+4=8\) soit \(\sqrt{\Delta }=2\sqrt 2\)

    \(x_1=\dfrac{-2+2\sqrt 2} 2=-1+\sqrt 2\)  et l'autre \(x_2=-1-\sqrt 2\) qui est hors de l'intervalle \([0;1]\) .

    \(a=1\)  et \(a>0\)  ce qui donne une parabole avec les branches orientées vers le haut :

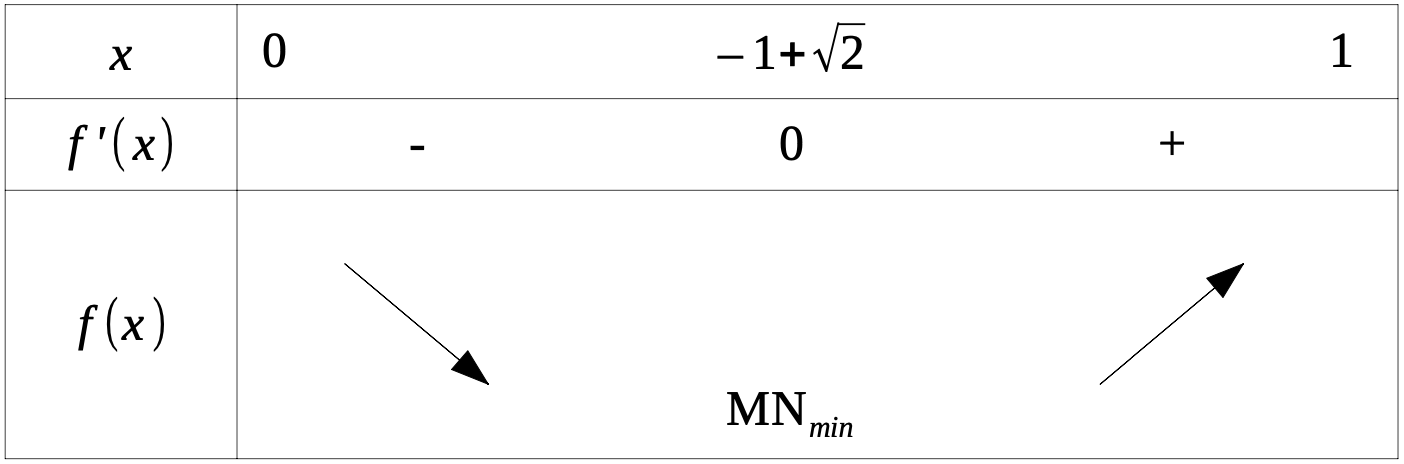
Partie C

  1. Il faut positionner le point \(\text M\)  tel que \(x=-1+\sqrt 2\) dm pour que \(\text{MN}\)  soit minimale.

    \(x\approx 0,41\) dm Soit \(4,1\) cm.

  2. \(\text{MN}_{\mathit{min}}=f(-1+\sqrt 2)=\dfrac{1+(-1+\sqrt 2)^2}{1-1+\sqrt 2}\)  Soit \(\text{MN}_{\mathit{min}}=f(-1+\sqrt 2)=\dfrac{1+1-2\sqrt 2+2}{\sqrt 2}=\dfrac{4-2\sqrt 2}{\sqrt 2}\).

    On multiplie par \(\sqrt 2\)  ce qui donne :

    \(\text{MN}_{\mathit{min}}=\dfrac{4\sqrt 2-4} 2=2\sqrt 2-2\) dm

    \(2\sqrt 2-2\approx 0,83\) dm soit \(8,3\) cm.