Devoir sur le produit scalaire

L'usage de la calculatrice est obligatoire.

Durée: 1h30

Exercice 1 (7 points)

Une figure directe est un polygone dont les points sont placés dans le sens contraire des aiguilles d'une montre.

\(\text{ABCD}\) est un carré direct de côté 1. On construit le triangle équilatéral direct \(\text{ABE}\), puis le carré direct \(\text{EBGH}\).

1. Construire la figure.

2. Que vaut l'angle \(\widehat{CBE}\) ?

   En déduire \(\overrightarrow{BC}\cdot\overrightarrow{BE}\) puis \(\overrightarrow{DA}\cdot\overrightarrow{BE}\).

3. Calculer \(\overrightarrow{EA}\cdot\overrightarrow{EB}\)

4. Démontrer que le triangle \(\text{BCG}\) est équilatéral. En déduire \(\overrightarrow{BC}\cdot\overrightarrow{BG}\) puis \(\overrightarrow{DA}\cdot\overrightarrow{EF}\)

5. Calculer \(\overrightarrow{AE}\cdot\overrightarrow{EF}\).

6. En utilisant la relation de Chasles, calculer \(\overrightarrow{DE}\cdot\overrightarrow{BF}\).

7. En déduire que les points \(\text{D}\), \(\text{E}\) et \(\text{G}\) sont alignés.

Exercice 2 (6 points)

Indiquer pour chaque question la réponse exacte. Aucune justification n'est demandée. Toute bonne réponse rapporte un point, et toute réponse erronée coûte un demi point.

1. \(\text{ABC}\) est un triangle équilatéral de côté 4. \(\text{I}\) et \(\text{H}\) sont les milieux respectifs de [AC] et [BC]. Le projeté orthogonal de \(\text{I}\) sur \((\text{AH})\) est le point \(\text{D}\). Alors:

   a. \(\overrightarrow{AB}\cdot\overrightarrow{AI}=\text{AH} \times \text{AD}\).

   b. \(\overrightarrow{AB}\cdot\overrightarrow{AI}=8\)

   c. \(\overrightarrow{AB}\cdot\overrightarrow{AI}=4\)

2. Sur la même figure, a. \(\overrightarrow{DC}\cdot\overrightarrow{AB}=0\)

   b. \(\overrightarrow{DC}\cdot\overrightarrow{DB}=0\)

   c. \(\overrightarrow{DA}\cdot\overrightarrow{BH}=0\)

3. \(\text{A}\), \(\text{B}\), \(\text{C}\) sont trois points non alignés tels que \(\overrightarrow{AB}\cdot\overrightarrow{AC}=8\) et \(\text{AC}=3\). Alors:

   a. \(\text{cos}(\widehat{ABC})=\dfrac 8 3\)

   b. \(\text{AB}=\dfrac 8 3\)

   c. \(\overrightarrow{AC}\cdot\overrightarrow{BC}=1\)

4. Dans un repère orthonormal, \(\overrightarrow{AB}(-4;3)\) et \(\overrightarrow{CB}(-1;5)\). Alors:

   a. \(\overrightarrow{AB}\cdot\overrightarrow{AC}=6\)

   b. \(\text{BC}=26\)

   c. \(\overrightarrow{BC}\cdot\overrightarrow{AB}=19\)

5. \(\text{ABC}\) est un triangle avec \(\text{AB}=4\), \(\text{BC}=6\) et \(\widehat{ABC}=40°\). Alors l'arrondi au centième de \(\text{AC}\) est:

   a. \(3,9\)

   b. \(15,23\)

   c. \(3,91\)

6. \(\text{ABC}\) est un triangle avec \(\text{AB}=3\), \(\text{AC}=5\) \(\text{BC}=6\). \(\text{I}\) est le milieu de \([\text{BC}]\). Alors:

   a. \(\text{AI}=4\)

   b. \(\text{AI}=2\sqrt{2}\)

   c. \(\text{AI}=\sqrt{26}\)

Exercice 3 (6 points)

\(\text{ABCD}\) et \(\text{AEFG}\) sont deux carrés, comme sur la figure ci-dessous. Les droites \((\text{DF})\) et \((\text{CE})\) se coupent en \(\text{I}\).

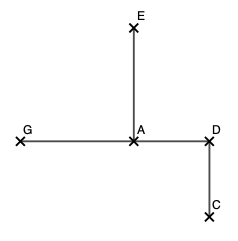
1. Compléter la figure. Que pensez-vous des droites \((\text{AI})\) et \((\text{DE})\) ?

2. On se place dans un repère orthonormal \((\text{A};\vec{\imath},\vec{\jmath})\) avec \(\vec{\imath}\) colinéaire à \(\overrightarrow{AD}\) et de même sens, et \(\vec{\jmath}\) colinéaire à \(\overrightarrow{AE}\) et de même sens. On suppose pour simplifier que \(\text{AD}=2\) et \(\text{AE}=3\).

   Donner les coordonnées des sommets des carrés.

3. Donner les coordonnées du vecteur \(\overrightarrow{FD}\), en déduire qu'une équation de la droite \((\text{DF})\) est \(3x+5y-6=0\).

4. Donner une équation de la droite \((\text{CE})\).

5. En déduire que les coordonnées de \(\text{I}\) sont \(\text{I}(\dfrac {18}{19};\dfrac{12}{19})\) et la preuve de la conjecture du 1.