Aller au contenu

Devoir sur le 2nd degré 2017-2018

L'usage de la calculatrice n'est pas autorisé.

Un soin particulier sera apporté à la rédaction de vos réponses.

Le barème est donné à titre indicatif, il peut donc évoluer.

Durée: 55 min

Exercice 1 (6 points)

Résoudre les équations suivantes:

a. \(3t-t^2+2=0\)

Corrigé

\(-t^2+3t+2=0\) est une équation du second degré, calculons son discriminant \(\Delta\):

\[\Delta=9+4\times 2=17\]

L'équation admet donc deux solutions: \(t_1=\dfrac{-3-\sqrt{17}}{-2}\) et \(t_2=\dfrac{-3+\sqrt{17}}{-2}\)

L'ensemble \(\text S\) des solutions de l'équation est donc: \(\text S=\left\{\dfrac{3-\sqrt{17}} 2\mathrm ;\dfrac{3+\sqrt{17}}2\right\}\) .

b. \(2x^3+x^2-3x=0\)

Corrigé

\(2x^3+x^2-3x=0 \Leftrightarrow x(2x^2+x-3)=0\)

\(2x^2+x-3\) est un trinôme du second degré qui admet \(1\) pour racine évidente, la deuxième racine s'obtient grâce à \(x_1x_2=\dfrac c a=\dfrac{-3} 2\). On a \(x_1=1\) donc \(x_2=-\dfrac 3 2\).

L'ensemble \(\text S\) des solutions de l'équation de départ est donc: \(\text S=\left\{-\dfrac 3 2\mathrm ;0\mathrm ;1\right\}\).

c. \(x-\dfrac 1 x=1\)

Corrigé

\(x-\dfrac 1 x=1 \Leftrightarrow x^2-1=x\) et \(x\neq 0 \Leftrightarrow x^2-x-1=0\) et \(x\neq 0\).

\(x^2-x-1\) est un trinôme du second degré, calculons son discriminant \(\Delta\).

\[\Delta=1+4=5\]

Ce trinôme admet donc deux racines: \(x_1=\dfrac{1-\sqrt 5} 2\) et \(x_2=\dfrac{1+\sqrt 5} 2\)

Ces racines étant non nulles, l'ensemble \(\text S\) des solutions de l'équation de départ est donc:

\[\text S=\left\{\dfrac{1-\sqrt 5} 2\mathrm ;\dfrac{1+\sqrt 5} 2\right\}\]

d. \(x+\sqrt{x-3}=9\)

Corrigé

\(x+\sqrt{x-3}=9 \Leftrightarrow 9-x=\sqrt{x-3} \Leftrightarrow (9-x)^2=x-3\) et \(x-3\geqslant 0\) et \(9-x\geqslant 0 \Leftrightarrow 81-18x+x^2=x-3\) et \(x\in [3\mathrm ;9] \Leftrightarrow x^2-19x+84=0\) et \(x\in [3\mathrm ;9]\) .

Résolvons l'équation \(x^2-19x+84=0\) :

C'est un trinôme du second degré, calculons son discriminant \(\Delta\):

\[\Delta=19^2-4\times 84=25=5^2\]

Les solutions de l'équation sont : \(x_1=\dfrac{19-5} 2=7\) et \(x_2=\dfrac{19+5} 2=12\).

Or \(x\in [3\mathrm ;9]\), l'ensemble \(\text S\) des solutions de l'équation de départ est donc:

\[\text S=\left\{7\right\}\]

Exercice 2 (6 points)

Soit \(f(x)=x^2+\mathit{mx}+m\) où \(m\) désigne un nombre réel.

  1. Pour quelle(s) valeur(s) de \(m\) le nombre 1 est-il une racine de \(f(x)\) ?

    Déterminer alors l'autre racine.

    Corrigé

    \(1\) est racine implique \(f(1)=0 \Rightarrow 1+2m=0 \Rightarrow m=-\dfrac 1 2\).

    On déduit la deuxième racine en sachant que \(x_1x_2=\dfrac m 1=m\) d'où \(x_2=m=-\dfrac 1 2\).

  2. Calculer le discriminant \(\Delta\) de \(f(x)\).

    Corrigé

    \(\Delta=m^2-4m=m(m-4)\)

  3. Avec un tableau de signe, déduire les valeurs de \(m\) pour lesquelles \(f(x)\) admet deux racines.

    Corrigé

    Tableau de signe

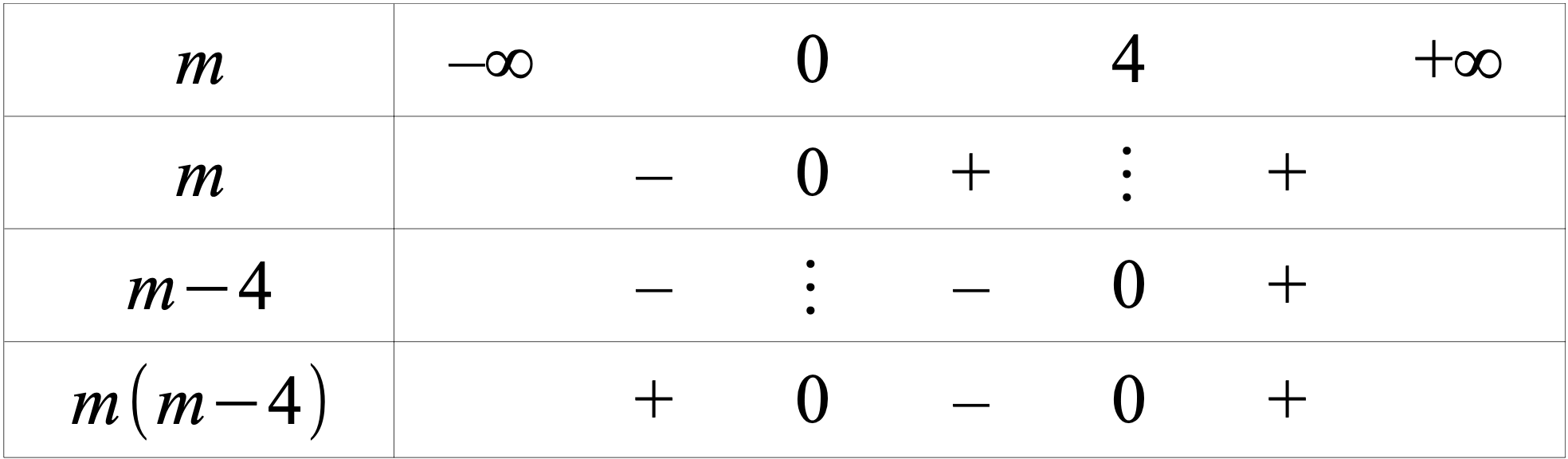
    \(f\) admet donc deux racines distinctes dans le cas où \(m\in ]0\mathrm ;4[\) (et une racine double si \(m=0\) ou \(m=4\).

  4. Mettre \(f(x)\) sous forme canonique. En déduire la valeur de l’extremum de \(f\) et préciser si c’est un minimum ou un maximum.

    Corrigé

    Forme canonique

    \[f(x)=\left(x+\dfrac m 2\right)^2-\dfrac{m^2} 4+m \]

    \(f(x)=\left(x+\dfrac m 2\right)^2-\dfrac{m^2-4m} 4\) \(f\) admet alors comme minimum \(\beta =-\dfrac{m^2-4m} 4\)

Exercice 3 (3 points)

  1. Déterminer deux nombres de somme 10 et dont la somme des carrés est 80.

    Corrigé

    On a \(a+b=10 \Rightarrow (a+b)^2=100 \Rightarrow a^2+b^2+2\mathit{ab}=100 \Rightarrow 2\mathit{ab}=100-a^2-b^2=100-(a^2+b^2)\)

    D'où \(2\mathit{ab}=20\) et \(\mathit{ab}=10\)

    On résout le système \(\left\{\begin{matrix}a+b=10\\\mathit{ab}=10\end{matrix}\right.\)

    Avec les propriétés de somme et produit des racines d'un trinôme du second degré, on obtient, \(a\) et \(b\) solutions de l'équation: \(x^2-10x+10=0\)

    Calculons le discriminant \(\Delta\) de cette équation: \(\Delta=10^2-40=60\)

    Les solutions s'écrivent alors: \(x_1=\dfrac{10-\sqrt{60}} 2\) et \(x_2=\dfrac{10+\sqrt{60}} 2\).

    D'où \(a=5-\sqrt{15}\) et \(b=5+\sqrt{15}\) ou le contraire.

  2. Si la somme de deux nombres est 10, quelle est la valeur minimale de la somme de leurs carrés ?

    Corrigé

    \(a+b=10 \Rightarrow b=10-a\), on étudie alors \(f(a)=a^2+(10-a)^2=2a^2-20a+100 \Rightarrow f(a)=2(a^2-10a+50) \Rightarrow f(a)=2((a-5)^2-25+50) \Rightarrow f(a)=2(a-5)^2+50\)

    Avec cette dernière expression de \(f\) il est clair que \(f(a)\geqslant 50\), or \(f(5)=50\)

    50 est donc le minimum de la somme des carrés et, dans ce cas, \(a=b=5\).